👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er
🌌上期文章:机器学习&&深度学习——从全连接层到卷积
📚订阅专栏:机器学习&&深度学习
希望文章对你们有所帮助
其实关于卷积的相关内容,包括一些实现之前已经介绍过且代码实现过,具体大家可以看我以前的这篇文章:
机器学习&&深度学习——torch.nn模块
顺便可以把池化层等等看一看。
下面要介绍卷积的多输入多输出通道,这是一个比较重要的内容。
卷积的多输入多输出通道
- 多输入通道
- 多输出通道
- 1×1卷积层
- 小结
多输入通道
当输入包含多个通道时,需要构造一个与输入数据具有相同输入通道数的卷积核,以便进行计算。
我们卷积核的每个输入通道包含形状为:
k
h
×
k
w
k_h×k_w
kh×kw
的张量。
而我们将所有的张量连结在一个就可以得到一个:
c
i
×
k
h
×
k
w
c_i×k_h×k_w
ci×kh×kw
的卷积核。
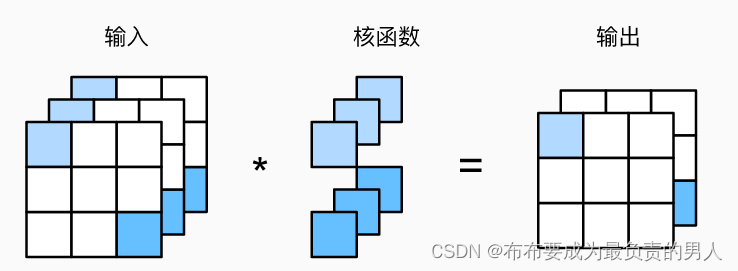
下面给出两个输入通道的互相关计算的图示:

我们实现一下多输入通道互相关运算,先定义好相关的函数:
import torch
from d2l import torch as d2l
def corr2d_multi_in(X, K):
"""先遍历X和K的第0个维度,再把它们加起来"""
return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
接着构造与上图相对应的X和K,验证输出:
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
print(corr2d_multi_in(X, K))
最终输出结果:
tensor([[ 56., 72.],
[104., 120.]])
多输出通道
随着神经网络层数的加深,我们常会增加输出通道的维数,通过减少空间分辨率以获得更大的通道深度,我们可以将每个通道看作对不同特征的响应(比如可以分别拿来分辨猫的耳朵、嘴巴、眼睛等等)。但是现实上更复杂,因为每个通道不是独立学习的,而是为了共同使用而优化的。因此,多输出通道并不仅是学习多个单通道的检测器。
为了获得多个通道的输出,我们可以为每个输出通道创建一个形状为:
c
i
×
k
h
×
k
w
c_i×k_h×k_w
ci×kh×kw
的卷积核张量,这样卷积核的形状就为:
c
o
×
c
i
×
k
h
×
k
w
c_o×c_i×k_h×k_w
co×ci×kh×kw
在互相关运算中,每个输出通道先获取所有输入通道,再以对应该输出通道的卷积核计算出结果。
如下我们实现一个计算多个通道的输出的互相关函数,通过将核张量K与K+1(K中每个元素加1)和K+2连接起来,构造了一个具有3个输出通道的卷积核。对输入张量X与卷积核张量K执行互相关运算:
import torch
from d2l import torch as d2l
def corr2d_multi_in(X, K):
"""先遍历X和K的第0个维度,再把它们加起来"""
return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
def corr2d_multi_in_out(X, K):
# 迭代“K”的第0个维度,每次都对输入“X”执行互相关运算。
# 最后将所有结果都叠加在一起
return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
K = torch.stack((K, K + 1, K + 2), 0)
print(corr2d_multi_in_out(X, K))
运行结果:
tensor([[[ 56., 72.],
[104., 120.]],
[[ 76., 100.],
[148., 172.]],
[[ 96., 128.],
[192., 224.]]])
1×1卷积层
看起来似乎没有多大意义。毕竟,卷积的本质是有效提取相邻像素间的相关特征,而1×1卷积显然没有这种作用,但其仍旧十分流行。
因为使用了最小窗口,1×1卷积失去了在高度和宽度维度上,识别相邻元素间相互作用的能力,其唯一计算实际上发生在通道上。
下面展示使用了具有3个输入通道和2个输出通道的1×1卷积核。其中,输入和输出具有相同的高度和宽度。
我们可以使用全连接层来实现1×1卷积(注意对输入和输出的数据形状进行调整),我们可以顺便验证它在执行1×1卷积时相当于之前实现的互相关函数:
import torch
from d2l import torch as d2l
def corr2d_multi_in(X, K):
"""先遍历X和K的第0个维度,再把它们加起来"""
return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
def corr2d_multi_in_out(X, K):
# 迭代“K”的第0个维度,每次都对输入“X”执行互相关运算。
# 最后将所有结果都叠加在一起
return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
def corr2d_multi_in_out_1x1(X, K):
c_i, h, w = X.shape
c_o = K.shape[0]
X = X.reshape((c_i, h * w))
K = K.reshape((c_o, c_i))
# 全连接层中的矩阵乘法
Y = torch.matmul(K, X)
return Y.reshape((c_o, h, w))
X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))
Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6
小结
1、多输入多输出通道可以用来扩展卷积层的模型。
2、当以每像素为基础应用时,1×1卷积层相当于全连接层。
3、1×1卷积层通常用于调整网络层的通道数量和控制模型复杂性。