目录

题目：

示例：

分析：

代码：

---

题目：

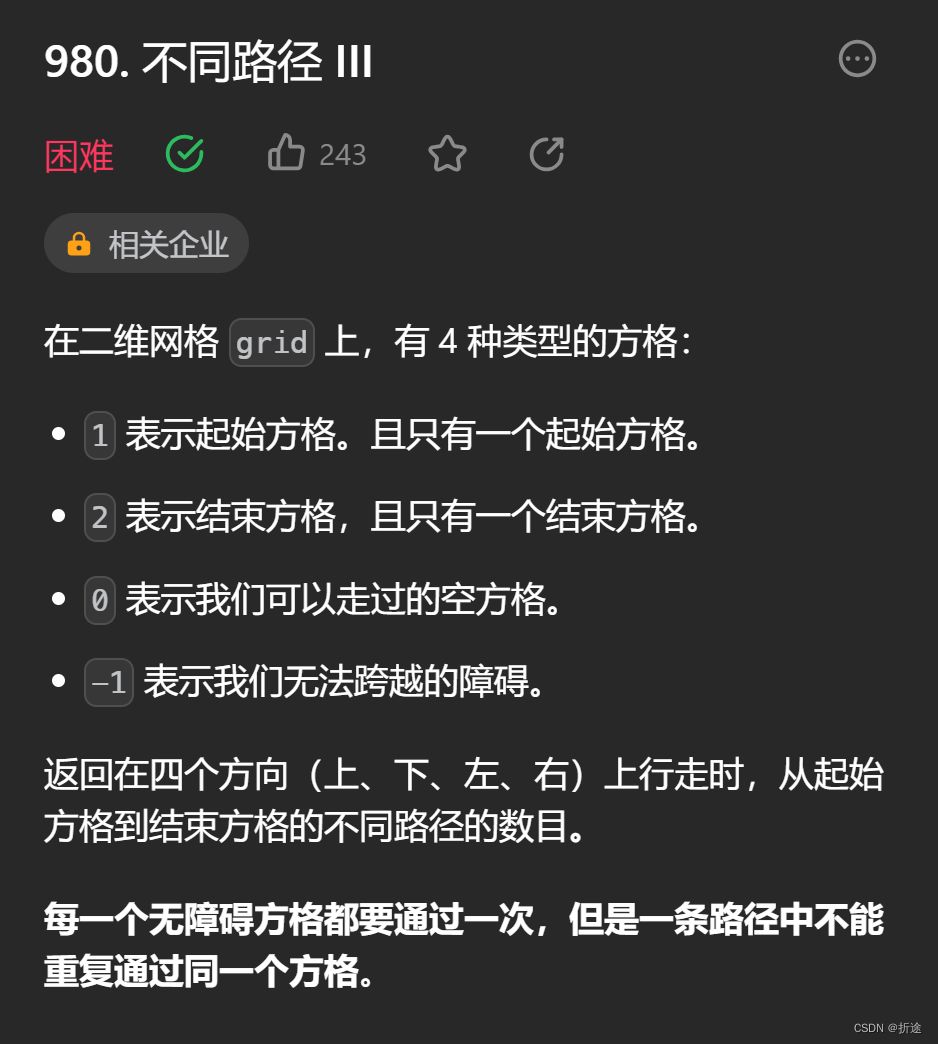
示例：

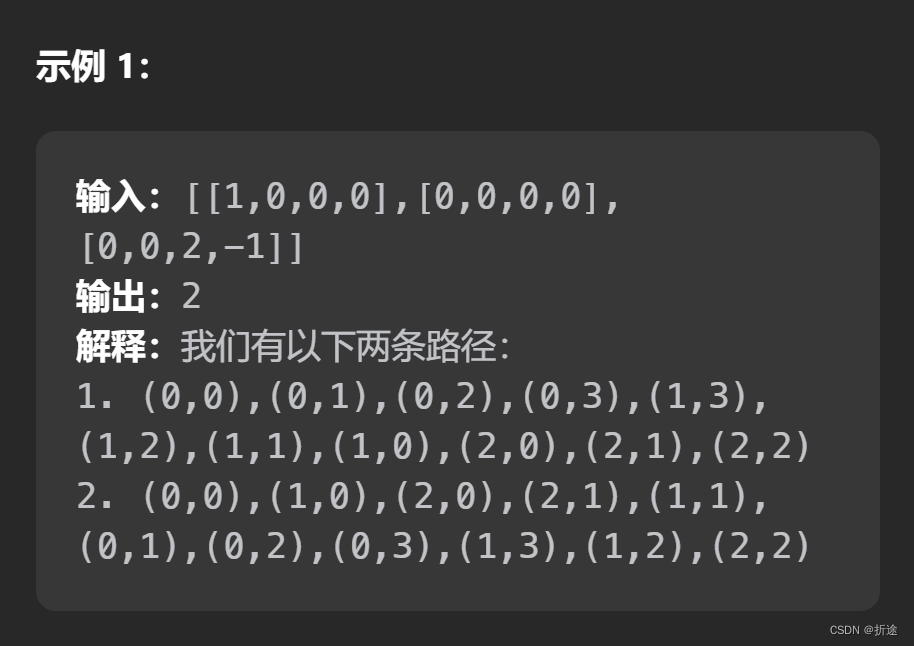
分析：

在二维网格之上，让我们模拟从开头走到末尾，并且要经过所有能经过的点，问我们有多少种走法。

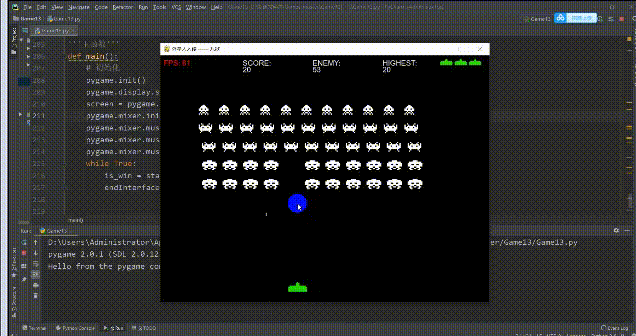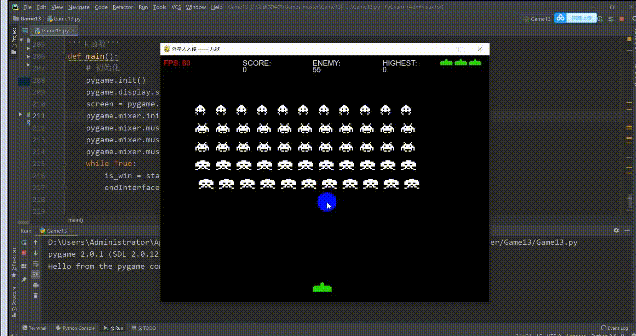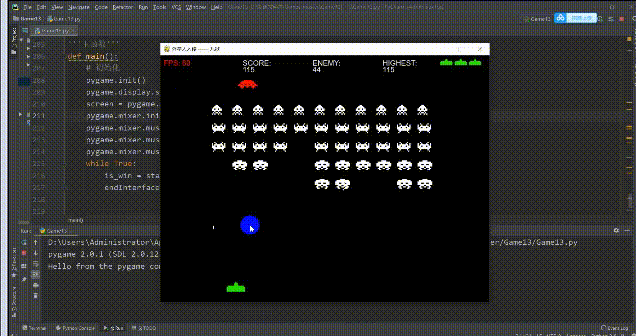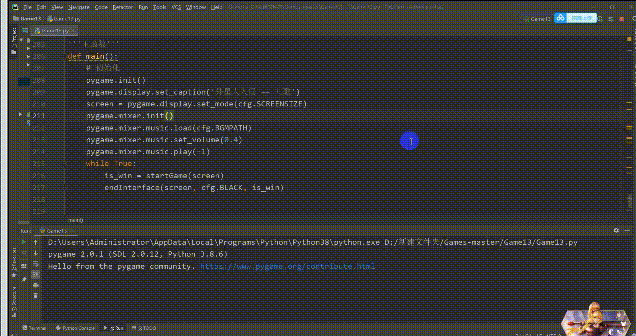
看到这道题我的第一个想到的就是那种一笔画的游戏 ，就类似这种：

那放到程序里面，我们则需要将数组转变为地图，题目给的条件是1是起点，2是终点，0是可以走的空格，-1是不能走的空格。

这种题目我们一般都是用的DFS也就是深度优先搜索以及回溯递归来做。

我们通过回溯递归来模拟行走，给递归函数传入地图数组的引用，并且再进入新一轮的递归前我们需要先把当前格子置为走过的路，这边我是置为了-1，跟不能走的路是一样的表示，这个是没问题的。

当走到终点2的时候，我们做一个检测，是不是以及把所有能走过的路都走过了，也就是查看我们最终的地图数组还有没有0，如果没有0，那就是说明没有没走过的路，那就是把所有路都走过了。

回溯类的题基本上都是一个模板，我们只需要处理要边界条件即可。

可以参考一下下面的动图，不过只是一部分（完整的过程弄出来太麻烦了）

代码：

class Solution {
public:
    int res=0;
    bool check(vector<vector<int>>& grid){  //检测是否没走过的路
        for(auto& gr:grid){
            for(auto& g:gr){
                if(g==0) return false;  //遇到了0(没走过的路)返回false.
            }
        }
        return true;
    }
    void digui(vector<vector<int>>& grid,int i,int j){
        if(i<0||j<0||i>=grid.size()||j>=grid[0].size()) return; //下标越界,直接返回
        if(grid[i][j]==2 && check(grid)) res++; //如果走到了终点,并且通过了检测,答案加1
        if(grid[i][j]!=0) return;   //不等于0(到了终点,到了走过的路,到了障碍)返回.
        grid[i][j]=-1;  //将当前地点标记为走过的路.
        digui(grid,i+1,j);  //往下走
        digui(grid,i,j+1);  //往右走
        digui(grid,i,j-1);  //往左走
        digui(grid,i-1,j);  //往上走
        grid[i][j]=0;   //回溯
    }

    int uniquePathsIII(vector<vector<int>>& grid) {
        for(int i=0;i<grid.size();i++){
            for(int j=0;j<grid[0].size();j++){
                if(grid[i][j]==1){
                    digui(grid,i+1,j);
                    digui(grid,i,j+1);
                    digui(grid,i,j-1);
                    digui(grid,i-1,j);
                    return res;
                }
            }
        }
        return res;
    }
};