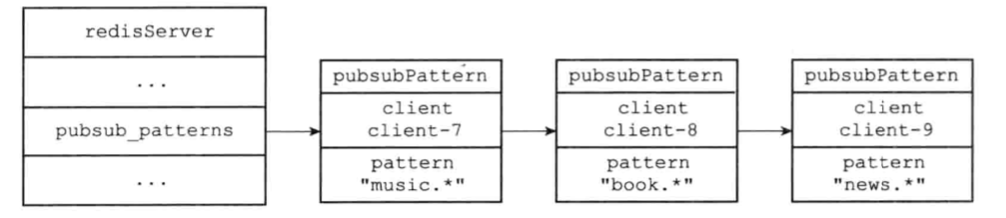
⛳向量的范数

范数的公式是向量每个分量 绝对值 P 次方 再用幂函数计算 P 分之一，这里 P 肯定是整数 1，2，3…到正无穷都是可以的 向量的范数就是把向量变成一个标量，范数的表示就是两个竖线来表示，然后右下角写上 P（范数的指数，用来表示不同的范数类型）范数是一个衡量向量大小的数学概念，它描述了向量中元素的大小和分布情况

符号和参数说明：

• P（范数的指数，用来表示不同的范数类型）
• ||x|| 表示向量 x 的范数（norm）
• ||表示去绝对值
• x表示向量
• xi表示向量中的每个分量
  

设维度n=2
红色的线是L1范数的几何意义， 也称为曼哈顿距离
绿色的线是L2范数的几何意义， 也成欧几里得距离

1范数是每个分量的绝对值加和，1范数写成L1

2 范数是每个分量的平方加和开根号， 其实代表的是向量的长度，高中时候学的向量的模，2 范数写成L2

范数在后面是非常有用的，在后面讲正则项的时候会用到

L1范数和L2范数是向量范数的两种常见形式，它们在机器学习和优化问题中有着重要的应用。它们的几何意义可以通过向量在几何空间中的表示来理解。

1. L1范数的几何意义：

L1范数，也称为曼哈顿范数，表示向量中各个元素绝对值之和。对于二维平面上的向量(x, y)，其L1范数为：||(x, y)||1 = |x| + |y|。在三维空间中，向量(x, y, z)的L1范数为：||(x, y, z)||1 = |x| + |y| + |z|。

L1范数的几何意义是从原点出发，沿着坐标轴的正方向移动到向量的末端，所经过的路径是由水平和垂直线段构成的。因此，L1范数可以理解为从原点到向量末端的曼哈顿距离。

在机器学习中，L1范数常用于稀疏性的推导和特征选择，因为L1范数对于某些情况下能够使得向量中的某些元素变为0，从而实现特征的稀疏表示。

2. L2范数的几何意义：

L2范数，也称为欧几里德范数，表示向量中各个元素的平方和的平方根。对于二维平面上的向量(x, y)，其L2范数为：||(x, y)||2 = √(x^2 + y^2)。在三维空间中，向量(x, y, z)的L2范数为：||(x, y, z)||2 = √(x^2 + y^2 + z^2)。

L2范数的几何意义是从原点出发，沿着直线路径移动到向量的末端。因此，L2范数可以理解为从原点到向量末端的欧几里德距离。

在机器学习中，L2范数常用于正则化项的添加，例如在岭回归中使用L2范数作为正则项，有助于防止过拟合并提高模型的泛化能力。

⛳L1、L2正则项

L1和L2正则项是在机器学习和统计中用于正则化的两种常见方式。

1. L1正则项（L1范数或Lasso正则化）：
   L1正则项是指将模型中参数的绝对值加入到损失函数中，用于惩罚模型参数的绝对值大小。它的数学表达式为：$$\lambda \sum _{i=1}^n|{\theta }_i|$$，其中λ是一个超参数，θi是模型的参数。L1正则项有助于产生稀疏的模型，即使其中一些参数的值为0，因为L1正则项的存在可以将某些参数收缩为0。

2. L2正则项（L2范数或岭回归）：
   L2正则项是指将模型中参数的平方加入到损失函数中，用于惩罚模型参数的大小。它的数学表达式为：$$\lambda \sum _{i=1}^n{\theta }_i^2$$，其中λ是一个超参数，θi是模型的参数。L2正则项有助于防止模型过拟合，并且不会使参数变为0，因此不会产生稀疏性。

在正则化中，损失函数通常由两部分组成：原始的目标函数（通常是最小化的损失函数）和正则项。目标是通过调整模型参数来平衡这两部分，以找到最佳的模型。

选择L1还是L2正则化取决于具体的问题和数据集。L1正则化通常用于特征选择和稀疏性处理，而L2正则化通常用于防止过拟合。有时也会同时使用L1和L2正则项，这被称为弹性网络正则化。

正则化和正则项是紧密相关的概念，它们通常用于控制机器学习模型的复杂度，并防止过拟合问题。

正则化是一种用于改善机器学习模型泛化能力的技术。在训练模型时，我们不仅希望模型能够很好地拟合训练数据，还希望它在未见过的数据上表现良好。过拟合是一种常见的问题，它指的是模型在训练数据上表现得很好，但在未知数据上表现较差的现象。

为了解决过拟合问题，引入了正则化的概念。正则化通过在模型的损失函数中添加一个正则项，惩罚模型的复杂度，从而限制模型的拟合能力。正则项通常是模型参数的范数（L1范数或L2范数），也可以是其他的复杂度度量。正则化的目的是在训练模型时平衡拟合训练数据和控制模型复杂度之间的关系，从而使模型具有更好的泛化能力。

在线性回归等模型中，正则化项可以写为：
$$\text{正则项}=\lambda \cdot ||\theta |{|}_p$$
其中，$||\theta |{|}_p$表示模型参数$\theta$的范数（可以是L1范数或L2范数），$\lambda$表示正则化参数，用于控制正则项的强度。

通过调整正则化参数$\lambda$的值，可以控制正则化项的影响程度。当$\lambda$较大时，正则化项的影响较强，模型的复杂度降低，有助于防止过拟合。当$\lambda$较小时，正则化项的影响较弱，模型的复杂度增加，有助于更好地拟合训练数据。

总的来说，正则化通过引入正则项来约束模型，使其更加简单和泛化能力更强，从而提高机器学习模型的性能。

🎯实战–求L1和L2范数

In [1]: import numpy as np

In [2]: W = np.array([3, 5, 6, 7, 8])

In [3]: np.abs(W)
Out[3]: array([3, 5, 6, 7, 8])

In [5]: np.sum(np.abs(W))
Out[5]: 29

In [6]: L1 = np.sum(np.abs(W))

In [7]: L1
Out[7]: 29

In [8]: np.square(W)
Out[8]: array([ 9, 25, 36, 49, 64])

In [10]: L2 = np.sum(np.square(W))

In [11]: L2
Out[11]: 183

In [13]: L2 = np.sqrt(np.sum(np.square(W)))

In [14]: L2
Out[14]: 13.527749258468683