---

---

前言

科研项目中要遇到蚁群 遗传 协同进化 粒子群等一些系列非确定性算法
所以总结一篇自己的学习笔记

---

一、蚁群算法是什么？

蚁群算法是模仿蚁群的寻食行为，在所有路径中，蚂蚁会随机挑选一个路径前进，等所有路径走完后会留下信息素，随着蚂蚁的增多，信息素的浓度与蚂蚁的数量和路径的长短成正比，蚂蚁更倾向于最短路径前进，此算法具有好的正反馈机制和自组织性。由原理描述可以看出良好的正反馈机制只限于后期，前期由于信息缺乏影响反馈机制的速度。

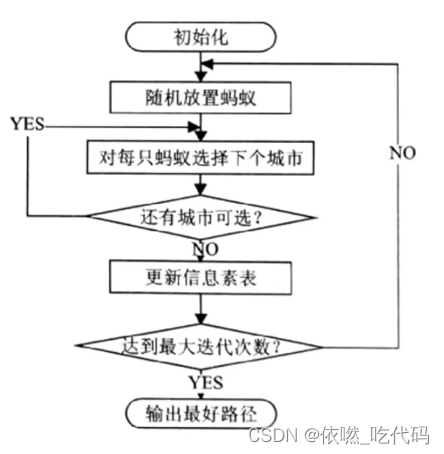
算法步骤

1、初始化(各个参数): 在计算之初需要对相关的参数进行初始化，如蚂蚁数量m、信息素因子α、启发函数因子β、信息素挥发因子ρ、信息素常数Q、最大迭代次数t等等。

2、构建解空间： 将各个蚂蚁随机地放置于不同的出发点，对每个蚂蚁k（k=1，2，……，m），计算其下一个待访问的城市，直到所有蚂蚁访问完所有的城市。

3、更新信息素： 计算各个蚂蚁经过的路径长度L，记录当前迭代次数中的最优解（最短路径）。同时，对各个城市连接路径上的信息素浓度进行更新。

4、判断是否终止： 若迭代次数小于最大迭代次数则迭代次数加一，清空蚂蚁经过路径的记录表，并返回步骤二；否则终止计算，输出最优解。

二、基本原理

根据信息素来进行判断
蚁群算法的基本原理来源于自然界蚂蚁觅食的最短路径原理，蚂蚁在寻找食物源时，能在其走过的路径上释放一种蚂蚁特有的分泌物–信息素，使得一定范围内的其他蚂蚁能够察觉到并由此影响他们以后的行为。**当一些路径上通过的蚂蚁越来越多时，其留下的信息素也越来越多，以致信息素强度增大，所以蚂蚁选择选该路径的概率也越高，从而更增加了该路径的信息素强度，这种选择过程被称为蚂蚁的自催化行为。**由于其原理是一种正反馈机制，因此，也可将蚂蚁王国理解为所谓的增强型学习系统。

三、数学模型

1、算法中的参数设置

2、构建路径

我们知道蚂蚁是根据信息素的浓度来判断所走的路线的，但是事实上，不是说哪条路的信息素浓度高蚂蚁就一定走哪条路，而是走信息素浓度高的路线的概率比较高。那么首先我们就需要知道蚂蚁选择走每个城市的概率，然后通过轮盘赌法（相当于转盘）确定蚂蚁所选择的城市。

轮盘赌

轮盘赌算法来自轮盘赌

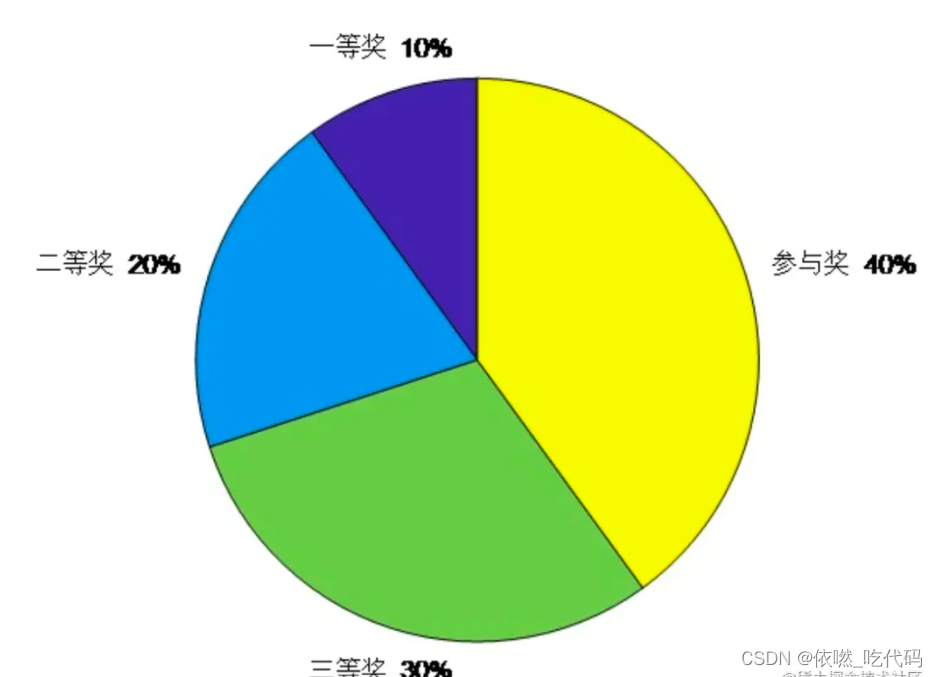
某个概率 = 某个因子 除以 所有因子之和
比如一等奖的因子是10，所有因子之和是 100，则一等奖的概率是 10%
学会了轮盘赌算法，让我们回到蚁群算法。
那么现在我们的目标是计算出蚂蚁去下个目的地的因子。因为蚂蚁走过的路上会留下信息素，信息素越高，选择这条路的概率越高，所以假定 因子 = 信息素。在这里，信息素就是一种变量，会在后续的反向传播环节中进行校准。
但是这样会带来一个问题，当第一次迭代完成后，走过的路上留下了信息素，没走过的路上没有信息素，导致之后的蚂蚁会更偏向于之前已经走过的路，而之前已经走过的路不一定是最优路线。
因此我们需要给因子再加一个参数，因为我们的问题是求最短路径，所以我们把两点之间的距离引入进来。从贪心的角度来说，两点之间距离越短，则选择这条路线的概率越大，所以我们乘上距离的倒数。
现在，因子 = 信息素 X （距离的倒数）
因子在受到多个参数影响后，我们希望能够调整各个参数的权重，在之前的人工神经网络中，我们是通过乘法的形式把权重和参数结合，即：
但是在这里我们已经使用了乘法，所以在处理权重时，我们可以使用指数，即：
因子信息素距离
这边使用 alpha 和 beta 分别代表 信息素 和 距离 的权重，这两个值属于常量，调参时可以灵活调整。
在求得每段路程的因子之后，每只蚂蚁使用轮盘赌算法去选择它要去的下个节点，遍历的时候顺便计算走过的路程，毕竟我们要求的就是最短路径。

蚂蚁k 从i到j的概率公式如下

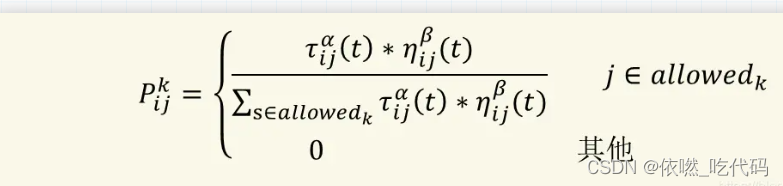
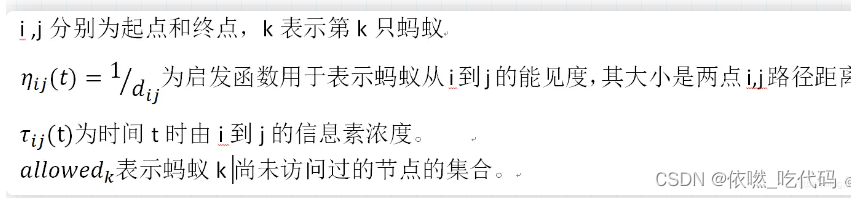
距离的倒数
蚂蚁选择城市的概率主要由𝜏ij (t)和𝜂ij (𝑡)有关，分母为蚂蚁k可能访问的城市之和（为常数），这样才能使蚂蚁选择各个城市的概率之后为1，符合概率的定义。𝜏ij (t)和𝜂ij (𝑡)上的指数信息素因子ɑ和启发函数因子𝛽只决定了信息素浓度以及启发函数对蚂蚁k从i到j的可能性的贡献程度。

例子

3、更新信息素浓度

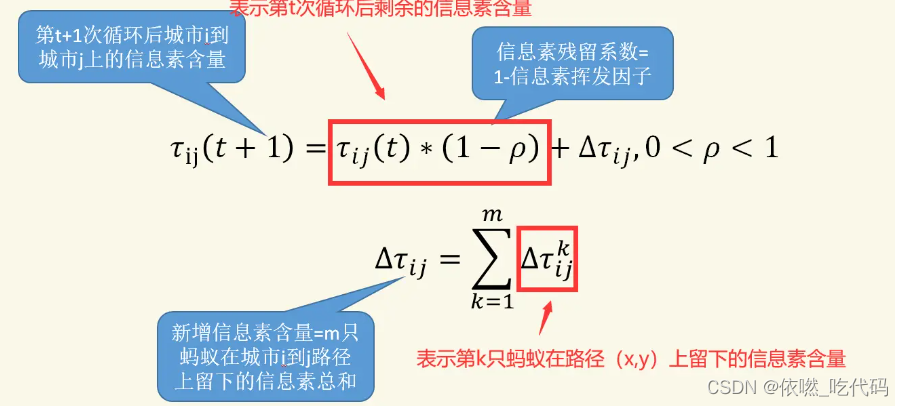
根据不同的规则我们可以将蚁群算法分为三种模型——蚁周模型(Ant-Cycle)、蚁量模型(Ant-Quantity)和蚁密模型(Ant-Density)。蚁周模型是完成一次路径循环后，蚂蚁才释放信息素，其利用的是全局信息。蚁量模型和蚁密模型蚂蚁完成一步后就更新路径上的信息素，其利用的是局部信息。本文章使用的是最常见的蚁周模型。

其中Q为信息素常量，Lk表示第k只蚂蚁在本次循环中所走路径的长度。
例：下图为信息素的更新过程，假设初始时各路径信息素浓度为10。

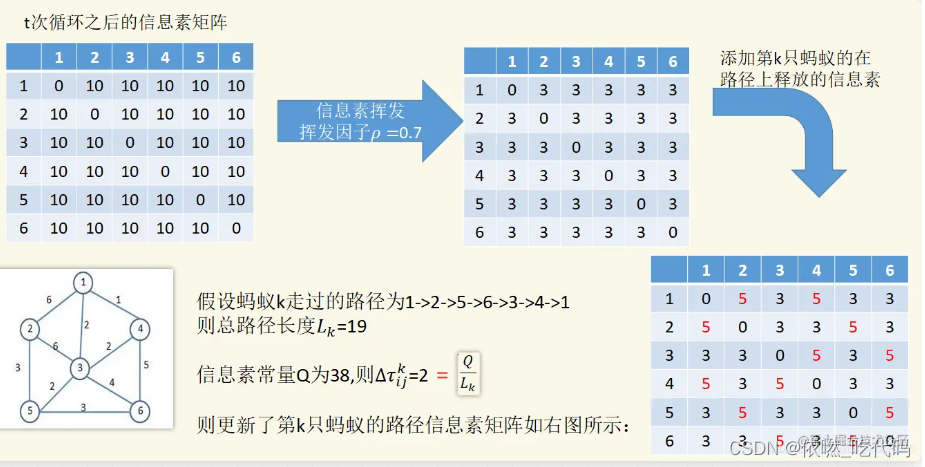
代码终止

蚁群算法中的终止条件：是否达到迭代次数。
一次迭代就是指m只蚂蚁都走完所有的城市，即存在m个搜索路径。
将所有路径进行比较，选择长度最短的路径，做出这一次迭代的可视化结果，更新信息素。并将当前的最短路径与过往的最短路径长度进行对比，同时迭代次数加1。
然后判断当前迭代次数是否等于设置的迭代次数。如果等于则停止迭代，否则进行下一次迭代。

四、代码展示

matlab 代码参考

五、参数实际设定

1.参数设定的准则

尽可能在全局上搜索最优解，保证解得最有型
算法尽快手链，以节省寻优时间
尽量反映客观存在的规律，以保证这种仿生算法的真实性

2.蚂蚁数量

一般设置蚂蚁数量为城市数的1.5倍比较稳妥

3.信息素因子

信息素因素a反映蚂蚁在运动过程中所积累的信息量在知道蚁群搜索中的相对重要程度。当a∈[1,4]时，综合求解性能较好

4.启发函数因子

启发函数因子b，反映了启发式信息在知道蚁群搜索过程中的相对重要程度，其大小反映了蚁群巡游过程中小言行、确定性因素的作用强度。b过大是，蚂蚁在某个局部点上选择局优的可能性大。b∈[3,4.5]，综合求解性能较好。

5.信息素挥发因子

信息素挥发因子ρ描述信息素的消失水平，而1-ρ则为信息素残留因子。ρ∈[0.2,0.5]时，综合求解能力较好

6. 最大迭代次数

一般去100-500

7. 组合参数设计策略

可按照一下策略来进行参数的组合设计：

确定蚂蚁数目，蚂蚁数目与城市规模之比约为1。5
参数粗调，即调整取值范围较大的a,b以及Q
参数微调，即调整取值范围较小的ρ

总结

蚁群算法有一下特点：

1、从算法的性质而言，蚁群算法是在寻找一个比较好的局部最优解，而不是强调全局最优解
2、开始时算法收敛速度较快，在随后寻优过程中，迭代一定次数后，容易出现停滞现象
3、蚁群算法对TSP及相似问题具有良好的适应性，无论城市规模大还是小，都能进行有效地求解，而且求解速度相对较快
4、蚁群算法解得稳定性较差，及时参数不变，每次执行程序都有可能得到不同界，为此需要多执行几次，已寻找最佳解。
5、蚁群算法中有多个需要设定的参数，而且这些参数对程序又都有一定的影响，所以选择合适的参数组合在算法设计过程中也非常重要。