此文GCN不是之前提到的lightGCN,而是真正的GCN图卷积,这个问题源于paper分类,同样是GAT所用的数据,其中paper之前的引用关系构成了图的边信息,之所以称之为半监督,并不是因为部分paper没有label及embedding信息,而是部分paper并没有他们的引用数据(只是出现在其他paper的引用中,如下的cite_paper,这句话是可议的,此文是逐渐明了的过程),如下释疑:q Group 277356808
1,证明paper个数总和为2708及有引用信息的paper个数(1565)Cora数据
dirs="~/cora"
print(os.listdir(dirs))
df=pd.read_csv(os.path.join(dirs,"cora.cites"),sep="\t",header=None)
print(df.head())
df.columns=["paper","cite_paper"]
lbe=LabelEncoder()
df["encoder"]=lbe.fit_transform(df["paper"])
a=lbe.classes_.tolist()
lbe = LabelEncoder()
lbe.fit(df["cite_paper"])
b=lbe.classes_.tolist()
total=list(set(a+b))
print("total papers %d"%len(total))
new=list(set(total).difference(a))
print("a %d, new %d"%(len(a),len(new)))附encoder编码代码:
dct=dict(zip(a,range(len(a))))
dct.update(dict(zip(new,range(len(a),len(a)+len(new)))))
df["paper"]=df["paper"].apply(lambda x:dct[x])
df["cite_paper"]=df["cite_paper"].apply(lambda x:dct[x])
df=df.groupby("paper")["cite_paper"].agg(list).reset_index()
print(df.shape)
print(df.head(2))2,读取label及embedding信息,证实所有的paper均有label及embedding
df = pd.read_csv(os.path.join(dirs, "cora.content"), sep="\t", header=None)
df.columns=["paper"]+["emb_"+str(i) for i in range(1433)]+["label"]
print(df.shape)
print(len(df["paper"].unique()))
not_in_total=list(set(total).difference(set(df["paper"].unique())))
print(not_in_total)#[]
not_have_label=list(set(df["paper"].unique()).difference(set(total)))
print(not_have_label)#[]#q Group 277356808总体来说还是有监督的学习,算不上严格的半监督,参考无监督学习,就是没有label的学习,半监督至少应该是有部分数据没有label,GCNpaper里面用的数据实际并不是如此,而仅仅是上述。那么paper中的表格label rate指的是啥呢?
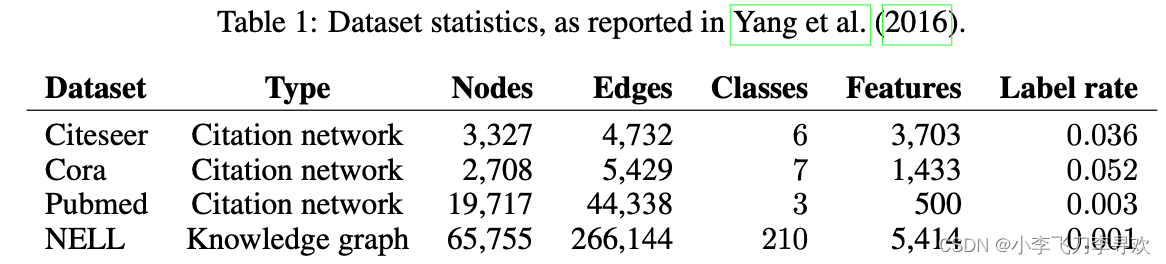
Label rate denotes the number of labeled nodes that are used for training divided by the total number of nodes in each dataset
难道说尽管实际数据是有label的,但并没有在训练中使用这部分数据,因为仅仅训练了140个,这个确实是的,so 140/2708=0.0516恰好与上面表格中的label rate对应,因此GCN paper的半监督算是严格意义的半监督。
GCN是啥结构呢?

简式如下:这是两层的GCN,通用式子就是A'*X*W ,这是一层的,其中参数如下
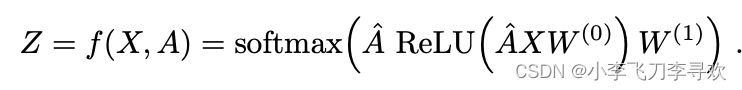


A是链接矩阵Adj,In是节点到节点自己的边信息,Dii是对角矩阵(因为是Adj,其值都是大于等于0的),因此D'求-1/2就是对单个数值进行-1/2,总体上来说是一种归一化,如下示例:python举例
>>> A34p
array([[3.2493546 , 4.1898723 , 4.0304203 , 3.9739053 ],
[2.699943 , 1.0808966 , 3.0756474 , 4.500847 ],
[1.6436101 , 2.258556 , 2.6459615 , 3.0535398 ],
[1.8343056 , 0.4629674 , 3.2731762 , 0.97009325]], dtype=float32)
>>> D33=A34p.sum(axis=-1)#277356808 QQ group
>>> D33
array([15.443553 , 11.357334 , 9.601667 , 6.5405426], dtype=float32)
>>> D33p=np.sqrt(D33)
>>> D33p
array([3.9298286, 3.3700645, 3.0986557, 2.5574484], dtype=float32)
>>> 1/D33p
array([0.25446403, 0.29673022, 0.3227206 , 0.39101472], dtype=float32)
>>> D33p=1/D33p#q Group 277356808
>>> np.mat(np.diag(D33p))*A34p*np.mat(np.diag(D33p))
matrix([[0.21040203, 0.3163654 , 0.33098125, 0.39540032],
[0.20386505, 0.09517168, 0.29452693, 0.5222148 ],
[0.13497454, 0.21628146, 0.27557313, 0.38532162],
[0.18251191, 0.0537162 , 0.4130372 , 0.14831999]], dtype=float32)但这种归一化与L2归一化不一样,从第一行的数值大小对比就能看出来,A34p 第一行第2个最大,而这种归一化后结果则是最后一个最大,如果值相差不大,那么最后的(也就是最近的)值可能会成为关键值,当然这个A的优化点可以尝试下L2norm。归一化的方式很多,不见得有啥效果。如下证实我的L2norm计算正确,
>>> A34p/np.tile(np.linalg.norm(A34p,ord=2,axis=-1,keepdims=True),[1,4])
array([[0.41896808, 0.54023737, 0.5196778 , 0.5123908 ],
[0.43698207, 0.17494163, 0.49778926, 0.72845584],
[0.33461118, 0.4598037 , 0.5386729 , 0.62164897],
[0.46996757, 0.11861691, 0.83862066, 0.24854766]], dtype=float32)
>>> from sklearn.preprocessing import Normalizer
>>> L2norm=Normalizer(norm="l2")
>>> L2norm.fit_transform(A34p)
array([[0.41896808, 0.54023737, 0.5196778 , 0.5123908 ],
[0.43698207, 0.17494163, 0.49778926, 0.72845584],
[0.33461118, 0.4598037 , 0.5386729 , 0.62164897],
[0.46996757, 0.11861691, 0.83862066, 0.24854766]], dtype=float32)因此综上:GCN总体上来说是对链接矩阵A做的优化,然后加入了DNN的思想,可以视为输入的X(节点embedding)与A相乘(视为线性转换)后再过DNN,这一步与SRGNN中将Adj视为权重w,然后再与节点embedding相乘后再过GRU是一样的,没有啥特别的。 因此GCN中“图”的概念也仅仅体现在adj,这与SRGNN是一样的。
顺便看下GCN代码, 我的处理结果与人家的对比是一致的(对adj的处理):官方代码是稀疏表示
>>> adj
array([[0., 0., 1., 0., 0., 0.],
[1., 0., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 1.],
[0., 0., 0., 1., 0., 0.],
[0., 0., 0., 0., 0., 0.]])
>>> transAdj(adj+np.diag([1,1,1,1,1,1]))#代码上面已提及
matrix([[0.5 , 0. , 0.5 , 0. , 0. ,
0. ],
[0.5 , 0.5 , 0. , 0. , 0. ,
0. ],
[0. , 0.5 , 0.5 , 0. , 0. ,
0. ],
[0. , 0. , 0.40824829, 0.33333333, 0. ,
0.57735027],
[0. , 0. , 0. , 0.40824829, 0.5 ,
0. ],
[0. , 0. , 0. , 0. , 0. ,
1. ]])
preprocess_adj(adj)#q Group 277356808
(array([[0, 0],
[2, 0],
[0, 1],
[1, 1],
[1, 2],
[2, 2],
[2, 3],
[3, 3],
[5, 3],
[3, 4],
[4, 4],
[5, 5]], dtype=int32), array([0.5 , 0.5 , 0.5 , 0.5 , 0.5 ,
0.5 , 0.40824829, 0.33333333, 0.57735027, 0.40824829,
0.5 , 1. ]), (6, 6))这一步正确了其他的dnn也无需啥操作,其实总体来说我也没有看到有明细的CNN操作,因为名字是图“卷积”,这个卷积应该体现在对adj的处理中,算是一种卷积滤波操作。
gcn原代码的操作也是matmul这种,或者dot,还是矩阵乘积,也就是W*X,W是随机初始化的,与我所述一致,dgl中的densegraphconv反而好看懂一些。
下面是本文的重点,数据的预处理方式,上一篇文章中没有完整给出adj的构建方式,有了网络结构没有数据处理方法,对于菜鸟来说还是不能拿来直接用。
注意:不是所有的分类任务都能用gcn,需要有图的结构才可以,我发现有提MNIST咋用GCN啊。。。一言难尽啊。当然可以强行构建图的关系,比如1,后面是2,2后面是3,这种可以自行尝试,不再赘述。
先来看如下数据hasItem.cfacts(部分,完整加群问我):为方便看出其中处理方法,先对第二列feat1编码,第三列视为feat2
hasItem s_10000008_16 close_analogue
hasItem s_10000008_12 thioguanine
...
hasItem s_10000047_24 liver_toxicity
....
hasItem s_10000112_20 solid_tumors
hasItem s_10000112_20 hodgkins_lymphoma
hasItem s_1000013_9 tamoxifen
hasItem s_1000013_2 summary
....读取后结果:
def read_cites(filename):
print ('reading cites')
cites, s_graph = [], dd(list)
for i, line in enumerate(open(filename)):
if i % 100000 == 0:
print ('reading cites {}'.format(i))
inputs = line.strip().split()
cites.append((inputs[1], inputs[2]))
s_graph[inputs[2]].append(inputs[1])
s_graph[inputs[1]].append(inputs[2])
return cites, s_graph
s_graph
defaultdict(<class 'list'>, {'close_analogue': ['2'], '2': ['close_analogue'], 'thioguanine': ['1', '16', '23', '70'], '1': ['thioguanine'], 'cross-resistance': ['0'],。。。。。。cites没啥好说的,s_graph就是其中的feat1和feat2相互做key-value而已,并且key一样时值为list,也就是key的value合并在一起。
读取list_features.txt
head -n 4 list_features1k.txt
s_10000008_16 1135 31 532789 1 145 13 1015 8 9325 16172 305 35709 5 338 1 120911 7 16227 6 0 193998 2575 141 2238 417099 170 14629 43 53015 5599 37410 14 14015 69 12998 33703 1563 202 5077 3999 1694 7208 3155 27235
s_10000008_12 1135 31 532789 1 145 13 1015 8 9325 16172 305 5 338 3383 12076 1 120911 7 16227 6 0 254 10937 1951 88301 20566 8469 45633 41911 3517 3072 117 5599 69 14 37410 87838 3003 113 15708 4235
s_10000008_10 1135 31 532789 1 145 13 1015 8 9325 305 35709 5 338 3383 12076 1 120911 7 16227 6 0 65 8469 100 12899 117964 117837 362082 3072 3058 5599 37410 14 30 69 33982 7141 317 8701 769
s_10000008_20 1135 31 532789 1 145 13 1015 8 9325 16172 305 35709 5 338 3383 12076 1 120911 7 6 0 376 370545 172 33 75 101 365182 379 42 5599 13940 69 14 37410 42043 11621 113 15305 1440
def read_features(filename):#277356808 QQ group
print ('reading features')
features, f_num = {}, 0
for line in open(filename):
inputs = line.strip().split()
features[inputs[0]] = []
try :
for t in inputs[1:]:
tt = int(t)
f_num = max(f_num, tt + 1)
features[inputs[0]].append(tt)
except Exception as error:
print(error)
return features, f_numfeatures是字典,key是上面的第一个字符串,values是list,就是每行除了第一个字符串后的整数,f_num是values中最大值+1,表示节点个数,此值与稀疏矩阵shape大小有关。
上述的s_graph似乎么有用,下面又重新编码整了一个,
def add_index(index, cnt, key):#277356808 QQ group
if key in index: return cnt
index[key] = cnt
return cnt + 1
def construct_graph(train_id, test_id, cites):
id2index, cnt = {}, 0
for id in train_id:
cnt = add_index(id2index, cnt, id)
for id in test_id:
cnt = add_index(id2index, cnt, id)
graph = dd(list)
for id1, id2 in cites:
cnt = add_index(id2index, cnt, id1)
cnt = add_index(id2index, cnt, id2)
i, j = id2index[id1], id2index[id2]
graph[i].append(j)
graph[j].append(i)
return graph构建x,tx,y,ty,t表示测试集,在下面的文件中的是训练集(也就是不带t的)
CATS = ['disease', 'drug', 'ingredient', 'symptom']这是类别,也就是4类。下面是读取上面文件的,也就是只读第3列
def read_train_labels(filename):
ret = []
for line in open(filename):
inputs = line.strip().split()
ret.append(inputs[2])
return ret train_list, in_labels = set(), dd(set)
for cat in CATS:#277356808 QQ group
print ("processing {}".format(cat))
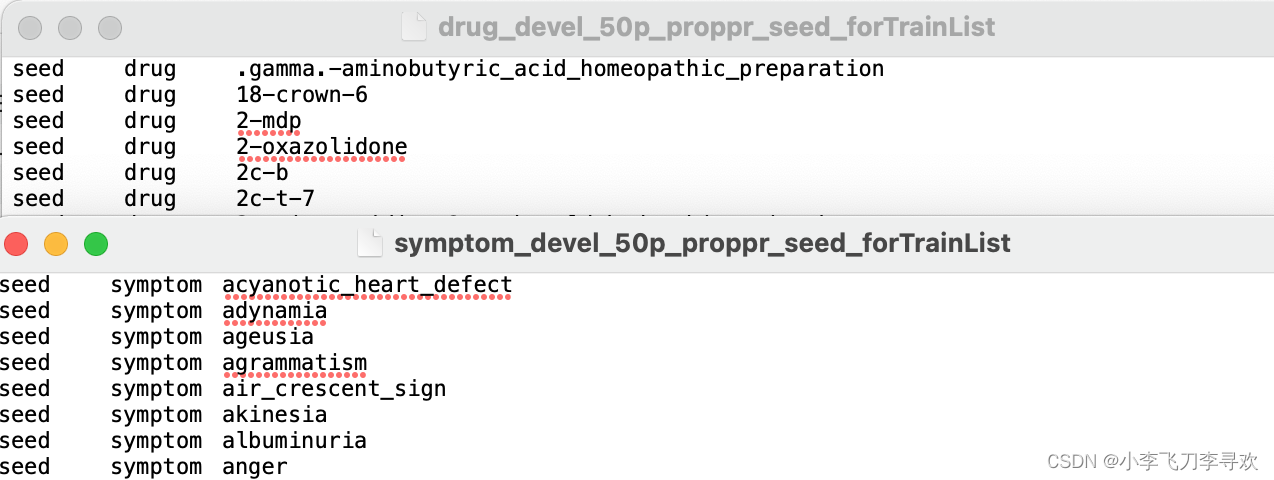
train_item = read_train_labels("{}/{}/{}_devel_50p_proppr_seed_forTrainList".format(dir, run_num, cat))
print("train_item",train_item)
for item in train_item:
for l in s_graph[item]:
train_list.add(l)
in_labels[cat].add(l)
print("train_list",train_list)
train_list是features中的key, 是hasItem.cfacts中的feat1
下面是train_list获得x,y的方法,tx,ty则是由test_list获取的,同样的函数
def construct_x_y(train_list, in_labels, features, f_num):
row, col = [], []
for i, ent in enumerate(train_list):
try:
for f_ind in features[train_list]:
row.append(i)
col.append(f_ind)
except:
pass
data = np.ones(len(row), dtype = np.float32)
x = sparse.coo_matrix((data, (row, col)), shape = (len(train_list), f_num), dtype = np.float32).tocsr()
y = np.zeros((len(train_list), len(CATS)), dtype = np.int32)
for i, ent in enumerate(train_list):
for j, cat in enumerate(CATS):
if ent in in_labels[cat]:
y[i, j] = 1
return x, y x, y = construct_x_y(train_list, in_labels, features, f_num)最终的graph则是由上述的train_list,test_list以及cites构成,上面已经提及此函数
construct_graph
但此codes并没有ind.cora.test.index 类似的文件,看了下其中是test文件的索引吧,也不是有序的
2692
2532
2050
1715
2362
2609
2622
1975
下面读取cora的文件,如下:
#cora.x#稀疏表示,pickle读取
print(data.shape,data[21].shape,data[12])
(140, 1433) (1, 1433)
(0, 51) 1.0
(0, 1005) 1.0
(0, 1175) 1.0
(0, 1216) 1.0
#元组第一个元素都是0,第二个元素最大为1432(?)
#cora.y
(140, 7) (7,) [0 0 0 0 1 0 0]#one-hot编码
#cora.tx
(1000, 1433) (1, 1433)
(0, 19) 1.0
(0, 217) 1.0
(0, 1209) 1.0
(0, 1218) 1.0
...
(0, 1291) 1.0
(0, 1361) 1.0
#cora.ty
(1000, 7) (7,) [0 0 0 1 0 0 0]
#cora.allx
(1708, 1433) (1, 1433)
(0, 51) 1.0
(0, 1005) 1.0
(0, 1175) 1.0
(0, 1216) 1.0
#cora.ally
(1708, 7) (7,) [0 0 0 0 1 0 0]
#graph
defaultdict(<class 'list'>, {0: [633, 1862, 2582], 1: [2, 652, 654], 2: [1986, 332, 1666, 1, 1454], 3: [2544], 4: [2176, 1016, 2176, 1761, 1256, 2175], 5: [1629, ... 2702: [186, 1536], 2703: [1298], 2704: [641], 2705: [287], 2706: [165, 2707, 1473, 169], 2707: [598, 165, 1473, 2706]})
adj = nx.adjacency_matrix(nx.from_dict_of_lists(graph))
print(adj)
(0, 633) 1
(0, 1862) 1
(0, 2582) 1
(1, 2) 1
(1, 652) 1
(1, 654) 1
(2, 1) 1
(2, 332) 1
(2, 1454) 1
(2, 1666) 1
(2, 1986) 1
..
(2706, 2707) 1
(2707, 165) 1
(2707, 598) 1
(2707, 1473) 1
(2707, 2706) 1读取新存储的数据(diel数据,下面脚本处理的数据):
#x #QQ group 277356808
(27, 1229796) (1, 1229796)
#y
(27, 4) (4,) [0 0 0 1]
#tx
(1767, 1229796) (1, 1229796)
#ty
(1767, 4) (4,) [0 0 0 0]
#graph
defaultdict(<class 'list'>, {157: [1794], 1794: [157], 1091: [1795], 1795: [1091, 252, 995, 328, 73, 1154, 1155, 1694, 815, 63, 482, 1329, 173, 763, 1658, 1283, 。。。 967: [2902], 2902: [967], 1163: [2903], 2903: [1163], 674: [2904], 2904: [674], 447: [2881], 688: [2881], 681: [2905], 2905: [681], 406: [2881], 1512: [1807], 41: [2557]})
#adj
(0, 1) 1
(1, 0) 1
(2, 3) 1
(3, 2) 1
(3, 41) 1
..
(2901, 2902) 1
(2902, 2901) 1
(2903, 2818) 1
(2904, 24) 1
(2905, 1942) 1数据中x的维度有问题,不符合cora中的维度,这种维度太大了,这个应该不会出现在实际问题中,因为它是输入数据的embedding,其他数据都是相符的。拜拜
愿我们终有重逢之时,而你还记得我们曾经讨论的话题
本文数据预处理脚本在此