1、统计学理论

1.1 大数定量

定义：
指大量重复某一实验时，最后的频率会无限接近于事件的概率
数据的样本量越大，我们预测和计算的概率就越准确
数据的样本量越小，我们预测和计算的概率就越可能失效
举例：
某产品用户还只有几百人，就用一个模型来预测用户的流失。数据量太小导致用上面模型都很难预测准确
样本量不足时，得出的预测结果是无序的，混乱的
解决方法：

• 主客观结合：深入业务，从用户的视角思考问题，广泛收集信息，不仅仅从数据中得出结论
• 想办法提升数据量级：想办法提升公司的业务和数据建设

结论：
对小样本数据得出的结论保持客观的怀疑和观察。并尽可能地在大样本量下进行分析

1.2 罗卡定律

定义：
凡两个物体接触，必会产生转移现象
凡有接触，必留痕迹
之前用于犯罪现场，指犯罪分子一旦来过现场，必会留下痕迹。现在主要用于针对用户行为的埋点和分析

结论：
在分析时，不要忘记尽可能的获取数据、挖掘更多的数据，从蛛丝马迹中找出数据背后的隐藏价值

1.3 幸存者偏差

飞机机翼事件
举例：
总体100万数据，你只取10万数据进行分析，分析出的结果也会更加偏向这10万数据的特征
结论：
各种分析的对象，能取全量尽可能取全量
不能取全量则要选择最能代表总体特征的要不
看别人的分析结果时，也要关注他是如何取样的

1.4 辛普森悖论

定义：
指的是两组分别讨论都满足某一性质的数据，一旦合并计算，会得出完全相反的结论
举例：

原因：虽然两组数据的总人数相同，但在不同类别上的人数分配上不均匀

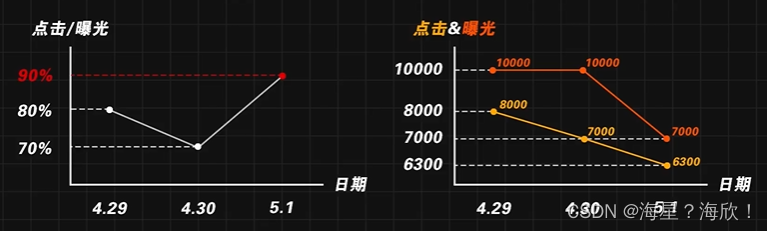
这里的点击/曝光 的比例上升，不是因为点击上升了，而是因为曝光下降的更快

结论：
不要在不同的权重下，更不要跨量级比较数据。否则很可能得出离谱结论
要得出正确的结论，首先要保证的是分析的数据在同一量级下

1.4 帕累托最优

一种资源分配的理想状态

认为仅通过调整分配方式，不增加资源就能提升生产效率
在实际中，常被用来分配渠道预算和业绩奖金

总结

• 大数定律：时刻对小样本数据得出的结论保持客观的怀疑和观察。并尽可能地在大样本量下进行分析
• 罗卡定律：用户的一切行为都会留下数据，要尽可能地拿来分析，这样才能找到数据背后隐藏的价值
• 幸存者偏差：分析时要提取检测取样偏差，所分析的样布要越能代表总体越好
• 辛普森悖论：一定要确保数据在同一量级和权重下，再进行分析
• 帕累托最优：就算不投入资源，也总有优化现状的方法

2、分析框架

2.1 一个原则：MECE法则

要求拆解出的各个部分都满足：相互独立、完全穷尽

2.2 方法

2.2.1 时间流程法：

• 经典AARRR模型（获取、激活、留存、收益、传播）
• PDCA（计划、执行、检测、处理）
• 精益创业模型

2.2.2 模型框架法

SWOT法（内部优势、劣势、外部机会、外部威胁）

2.2.3 量化公式法

2.2.4 穷尽要素法

3、量化问题为数据

属性：描述分析对象有哪些特征
绝对值：衡量一件事最后的结果
转化率：衡量一个环节的完成度

4、经典场景的应用

业务诊断：针对现在发生的问题找原因，对应是什么？为什么？
业务增长：需要给出系统量化的业务增长策略，对应怎么做？做多少？

4.1 业务诊断

基于现有的业务模式，进行优化
举例：
8月份某音乐APP的会员收入，相较于7月份下跌了。

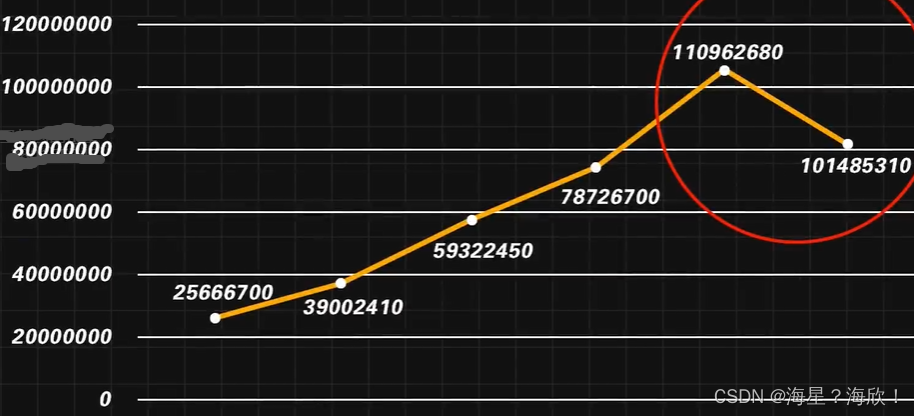
灵活组和各种方法

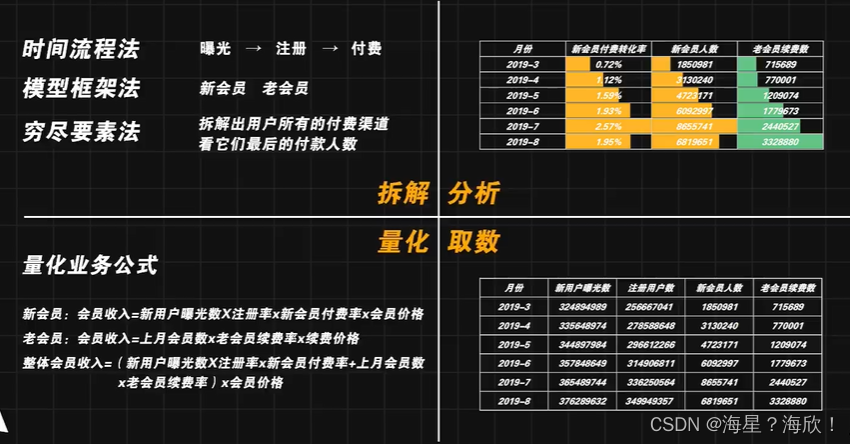
基于业务拆解，先有时间流程法拆解出必要的流程环节：曝光，注册，付费三个环节。
新老用户在付费动机上是完全不同的。新会员更多的是体验一下，新会员需要投放拉新才能获得；老会员一般是有需求或者体验好才付费的。而老会员天然活跃在APP上。所以后续分析过程中，两者最好区分出

串联指标，量化业务公式。对于新用户，会员收入=。。。。

不断循环，拆解、量化、取数、分析的整套流程

4.2 业务增长

重新设计业务模式

5 数据分析的作用

数据分析解决的问题：是什么？为什么？怎么做？做多少？

是什么？
用数据去量化企业当前的经营现状或者业务事实

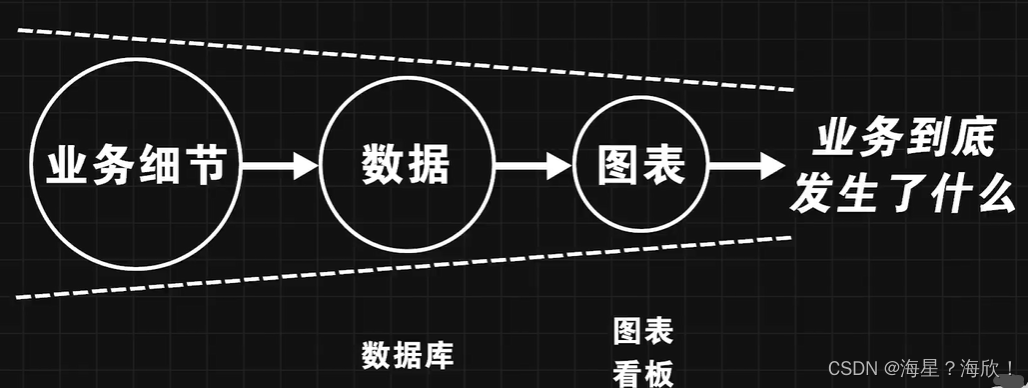
为什么？
看数据-分析原因

怎么做？

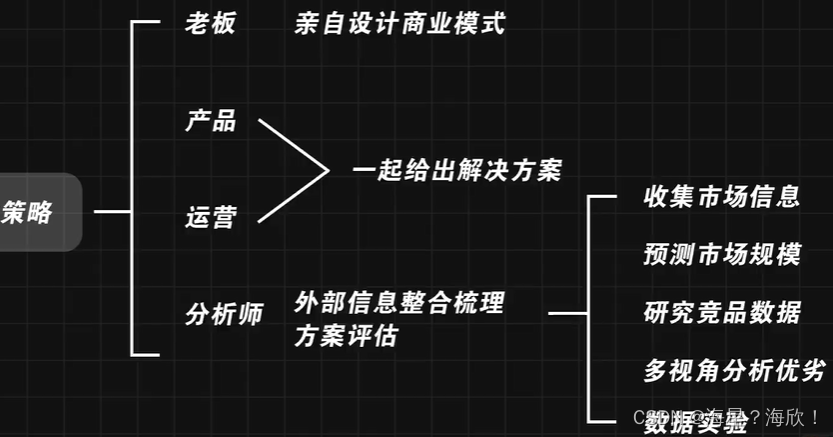
沟通时，确认问题：

统计口径！
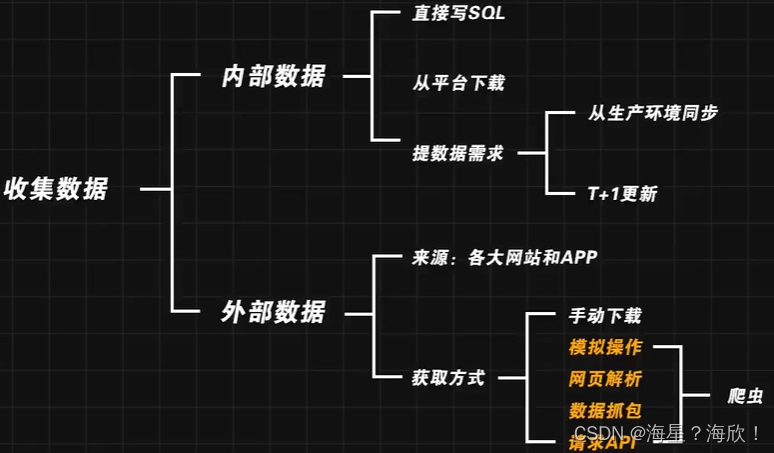
收集数据：