24考研数据结构-二叉树的遍历

news2025/1/18 21:05:21

5.3二叉树的遍历和线索二叉树
- 数据结构：树的遍历
- - 前序遍历
  - 中序遍历
  - 后序遍历
  - 层次遍历
  - 遍历方法的选择
  - 结论
- 树的遍历应用
- 5.3.1二叉树的遍历
- - 1. 先序遍历（根左右 NLR）
  - 2. 中序遍历（左根右 LNR）
  - 3. 后续遍历（左右根 LRN）
  - 4. 求树的深度（递归应用）
  - 5. 非递归遍历
  - 6. 层次遍历
  - 7. 由遍历序列构造二叉树

5.3二叉树的遍历和线索二叉树

数据结构：树的遍历

在计算机科学中，树是一种常见的数据结构，它由节点组成，每个节点可以有零个或多个子节点，形成了一个层次结构。树的遍历是指按照一定规则遍历树的所有节点，以便访问和处理节点的数据。树的遍历有多种方法，包括前序遍历、中序遍历、后序遍历和层次遍历。本文将对这四种遍历方法进行介绍和比较。

前序遍历

前序遍历是一种深度优先的遍历方法，它首先访问根节点，然后按照从左到右的顺序依次遍历根节点的所有子树。具体步骤如下：

访问根节点。
对根节点的每个子树，递归执行前序遍历。

前序遍历的遍历顺序为：根节点 -> 左子树 -> 右子树。

中序遍历

中序遍历也是一种深度优先的遍历方法，它按照从左到右的顺序遍历根节点的所有子树，并在遍历完左子树后访问根节点，最后遍历右子树。具体步骤如下：

对根节点的左子树，递归执行中序遍历。
访问根节点。
对根节点的右子树，递归执行中序遍历。

中序遍历的遍历顺序为：左子树 -> 根节点 -> 右子树。

后序遍历

后序遍历是一种深度优先的遍历方法，它首先按照从左到右的顺序遍历根节点的所有子树，然后访问根节点。具体步骤如下：

对根节点的每个子树，递归执行后序遍历。
访问根节点。

后序遍历的遍历顺序为：左子树 -> 右子树 -> 根节点。

层次遍历

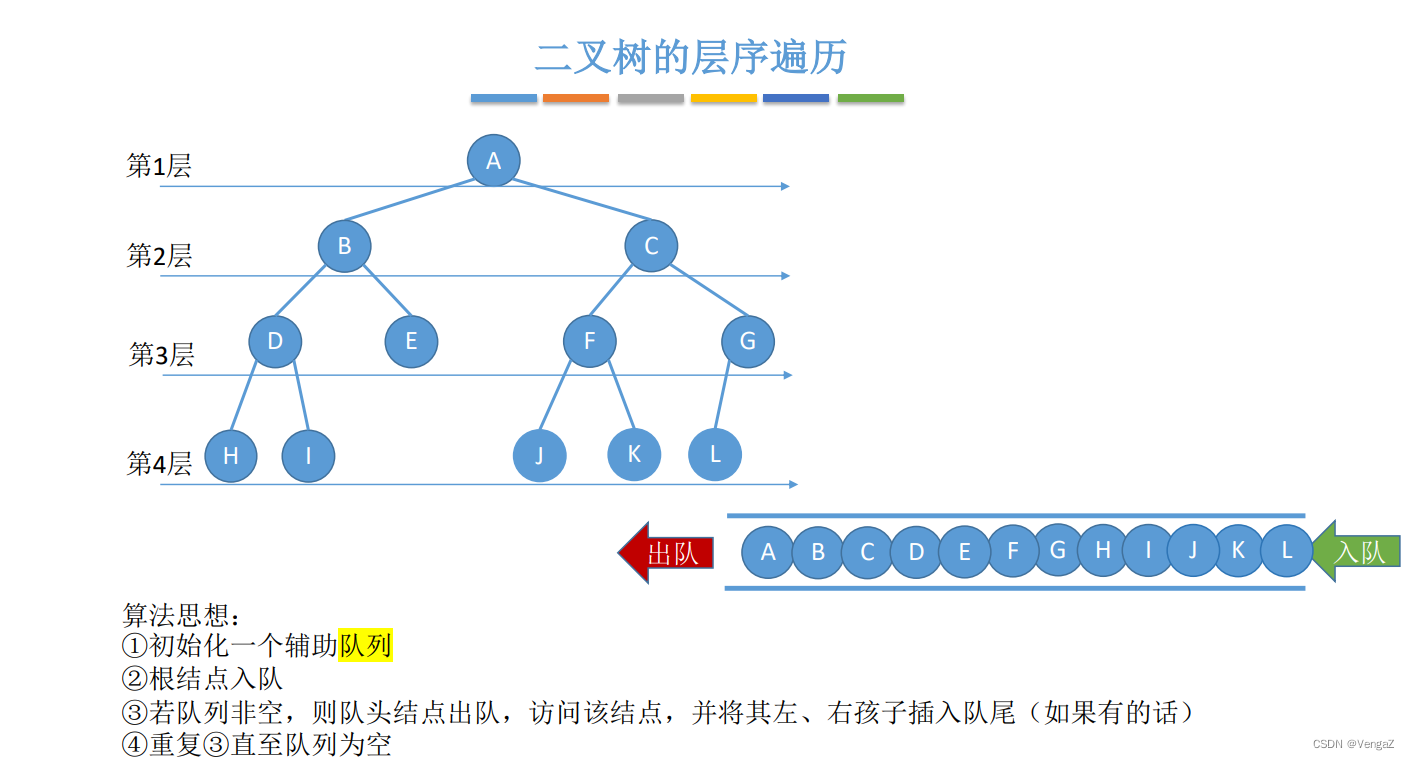
层次遍历是一种广度优先的遍历方法，它按照从上到下、从左到右的顺序逐层遍历树的节点。具体步骤如下：

从根节点开始，将根节点入队。
当队列不为空时，循环执行以下步骤：
- 出队一个节点，并访问该节点。
- 将该节点的所有子节点入队。

层次遍历的遍历顺序为：根节点 -> 第二层节点 -> 第三层节点 -> … -> 最后一层节点。

遍历方法的选择

在实际应用中，选择不同的遍历方法取决于对数据的需求和处理方式。如果需要按照树的层次结构处理数据，层次遍历是一个较好的选择。而如果需要对树的节点进行某种特定顺序的处理，可以考虑使用前序、中序或后序遍历。根据不同的情况，可以灵活地选择合适的遍历方法。

结论

树是一种重要的数据结构，在处理树的数据时，遍历是一种常用的操作。前序遍历、中序遍历、后序遍历和层次遍历是常见的树的遍历方法，它们各自有着不同的遍历顺序和应用场景。在实际应用中，根据对数据的需求和处理方式，可以灵活地选择合适的遍历方法来处理树的节点数据。

树的遍历应用

树的遍历在很多实际应用中都有着重要的作用。以下是树的遍历应用的一些例子：

查找特定节点： 可以使用中序遍历在二叉搜索树中查找特定节点。
树的复制： 可以使用前序遍历来复制一棵树。
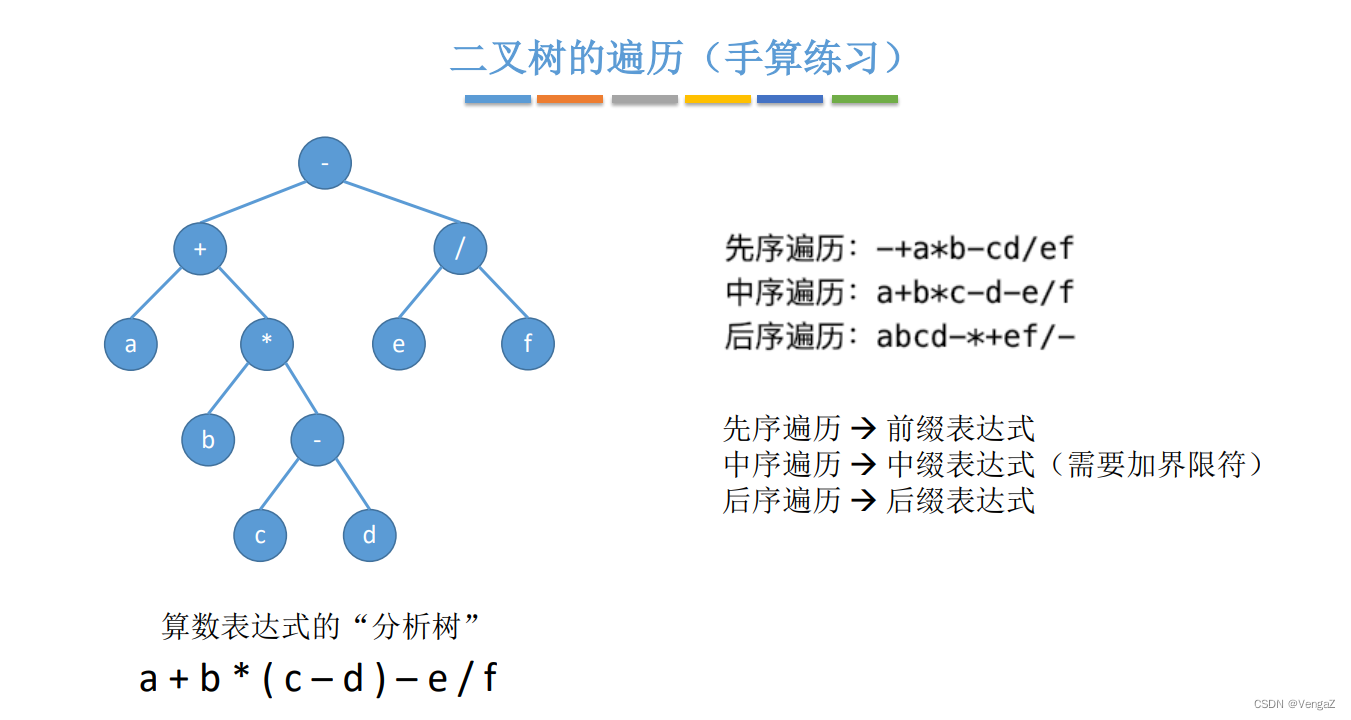
表达式求值： 可以使用后序遍历在二叉树表示的表达式中进行求值。
文件系统遍历： 文件系统可以被表示为一棵树，通过遍历文件系统树，可以对文件进行管理和处理。
图的遍历： 图可以看作是特殊的树结构，对图进行遍历可以用于寻找路径等应用。

5.3.1二叉树的遍历

在这里插入图片描述

1. 先序遍历（根左右 NLR）

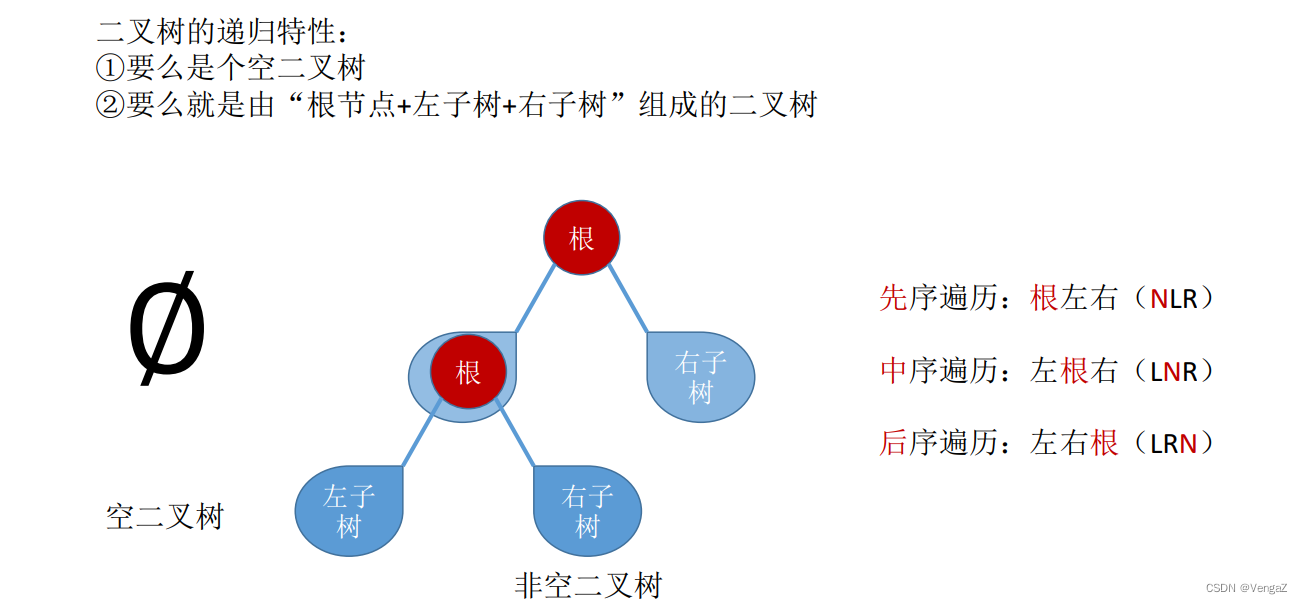
若二叉树为空，不用操作

若二叉树非空：

访问根节点
先序遍历左子树
先序遍历右子树

typedef struct BiTnode{
   ElemType data;          
   struct BiTNode *lchild, *rchild; 
}BiTNode, *BiTree;

void PreOrder(BiTree T){
   if(T!=NULL){
      visit(T);                 //访问根结点
      PreOrder(T->lchild);      //递归遍历左子树
      PreOrder(T->rchild);      //递归遍历右子树
   }
}

2. 中序遍历（左根右 LNR）

若二叉树为空，不用操作

若二叉树非空：

先序遍历左子树
访问根节点
先序遍历右子树

typedef struct BiTnode{
   ElemType data;          
   struct BiTNode *lchild, *rchild; 
}BiTNode, *BiTree;

void InOrder(BiTree T){
   if(T!=NULL){
      InOrder(T->lchild);       //递归遍历左子树
      visit(T);                 //访问根结点
      InOrder(T->rchild);       //递归遍历右子树
   }
}

3. 后续遍历（左右根 LRN）

若二叉树为空，不用操作

若二叉树非空：

先序遍历左子树
先序遍历右子树
访问根节点

typedef struct BiTnode{
   ElemType data;          
   struct BiTNode *lchild, *rchild; 
}BiTNode, *BiTree;

void PostOrder(BiTree T){
   if(T!=NULL){
      PostOrder(T->lchild);       //递归遍历左子树    
      PostOrder(T->rchild);       //递归遍历右子树
      visit(T);                 //访问根结点
   }
}

4. 求树的深度（递归应用）

在这里插入图片描述

5. 非递归遍历

先序遍历
中序遍历
后序遍历

6. 层次遍历

在这里插入图片描述

//二叉树的结点(链式存储)
typedef struct BiTnode{
   ElemType data;          
   struct BiTNode *lchild, *rchild; 
}BiTNode, *BiTree;

//链式队列结点
typedef struct LinkNode{
   BiTNode * data;
   typedef LinkNode *next;
}LinkNode;

typedef struct{
   LinkNode *front, *rear;  
}LinkQueue;

//层序遍历
void LevelOrder(BiTree T){
   LinkQueue Q;
   InitQueue (Q);          //初始化辅助队列
   BiTree p;
   EnQueue(Q,T);           //将根节点入队
   while(!isEmpty(Q)){     //队列不空则循环
      DeQueue(Q,p);        //队头结点出队
      visit(p);            //访问出队结点
      if(p->lchild != NULL)
         EnQueue(Q,p->lchild);   //左孩子入队
      if(p->rchild != NULL)
         EnQueue(Q,p->rchild);   //右孩子入队
   }
}