路径总和 I ：

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

要点：判断是否存在满足条件的路径，只需返回true or false。

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。 

解题思路：

每遍历一个节点，就从targetsum中减去当前节点的值，当遍历到叶子节点时，如果targetsum=0，说明存在该路径，返回true。反之，返回false

class Solution {
public:
    
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root==nullptr) return false;
        targetSum-=root->val;
        if(root->left==nullptr&&root->right==nullptr)
        {
            return targetSum==0;
        }
        //左子树和右子树有一个满足就可以，所以用||的关系
        return hasPathSum(root->left,targetSum)||hasPathSum(root->right,targetSum);
    }
};

 

路径总和 II：

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

要点：返回所有满足题意的路径，必须是从根节点开始，叶子节点结束。

 

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

解题思路：

 添加一个临时数组，用来存放当前遍历到的节点走过的路径。其他的与第一题相同，找到符合题意的路径，就将临时数组存放到结果数组中，若不符合条件，需回退，注意回退时需要将将一个放到临时数组中的节点删掉。

class Solution {
public:
    vector<vector<int>> res;//所有路径
    vector<int> temp;//当前路径
    void dfs(TreeNode* root, int targetSum)
    {
        if(root==nullptr) return;
        temp.push_back(root->val);//当前节点放入到temp中
        targetSum-=root->val;//从总和中减去
        //若遇到叶子节点，需判断目标值是否已经为0
        if(root->left==nullptr&&root->right==nullptr)
        {
            //目标值=0，说明当前路径符合题意，temp放到res中
            if(targetSum==0)
            {
                res.push_back(temp);
            }
        }
        //递归
        dfs(root->left,targetSum);
        dfs(root->right,targetSum);
        //不符合题意，将当前节点从路径中删掉
        temp.pop_back();
    }
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        dfs(root,targetSum);
        return res;
    }
};

路径总和 III:

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

要点：返回的是所有符合题意的路径总条数，与第二题不一样的是，可以不是从根节点开始，也不需要在叶子节点结束。

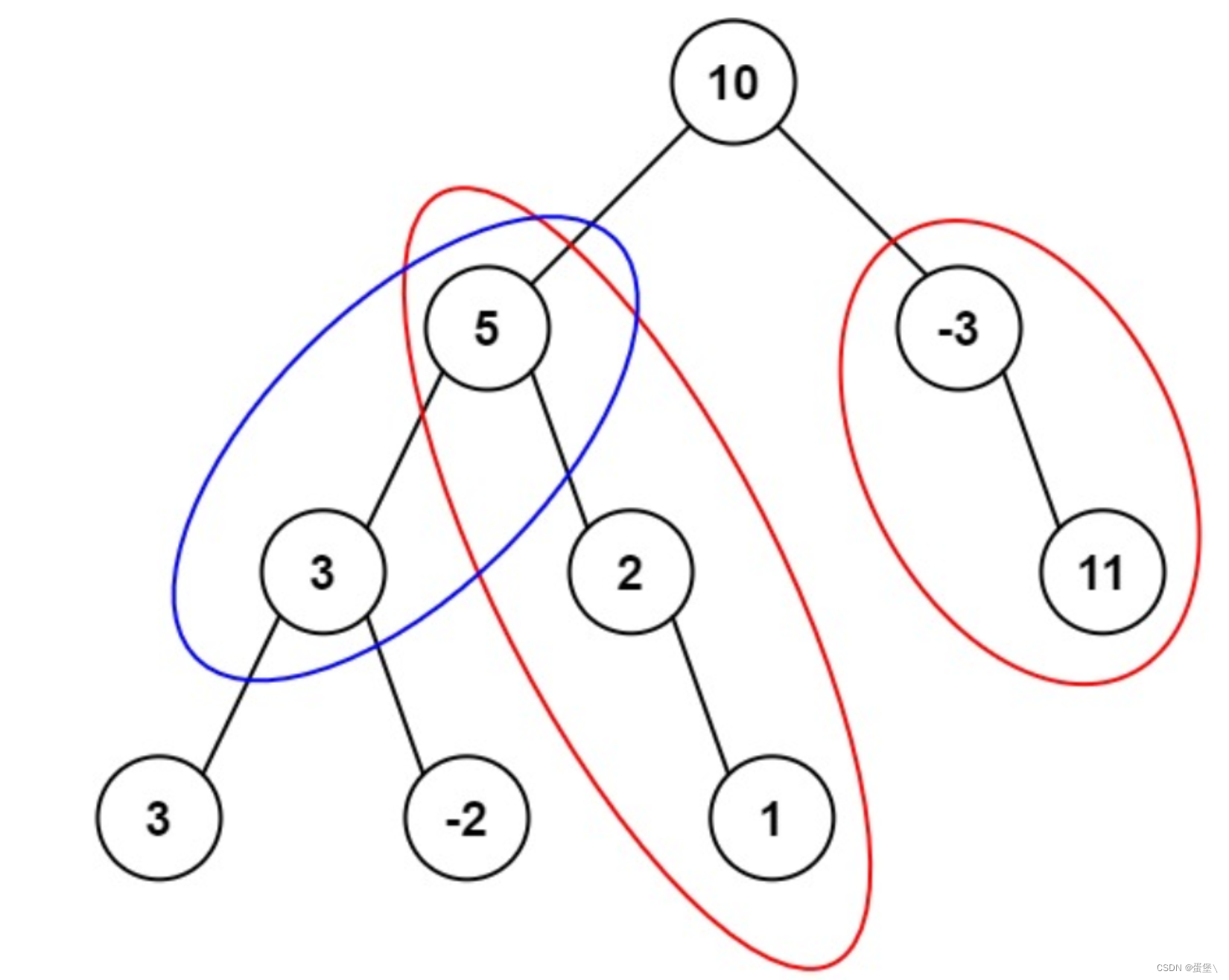
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。 

解题思路：

相当于是递归套递归，构建一个找路径函数，遍历以当前节点为起始的路径中，是否存在符合题意的路径，然后再在原函数递归到每一个节点，使每一个节点都为起始节点进行找符合题意的路径。

class Solution {
public:
    int res=0;
    int pathSum(TreeNode* root, int targetSum) {
        if(root==nullptr) return res;
        find_path(root,targetSum);//以当前的root节点为起始节点，找路径
        pathSum(root->left,targetSum);//递归当前根节点的左子树上的节点
        pathSum(root->right,targetSum);//递归当前根节点的右子树上的节点
        return res;
    }
    //找路径函数
    void find_path(TreeNode* root,long targetSum)
    {
        if(root==nullptr) return;

        targetSum -= root->val;
        if(targetSum==0)//只要targetsum=0，说明存在一条路径，那么res++
        {
            res+=1;
        }
        find_path(root->left,targetSum);
        find_path(root->right,targetSum);
    }
};