Vital nodes identification in complex networks
- 识别单个重要节点的方法
- 基于结构信息
- 一、结构中心性(Structural centralities)
- 1.度中心性(基于邻域的中心性)
- 2.四阶邻居信息(基于邻域的中心性)
- 3.ClusterRank(基于邻域的中心性)
- 4.Coreness(基于邻域的中心性)
- 5.H-index(基于邻域的中心性)
- 6.Eccentricity离心率(基于路径中心)
- 6.Closeness centrality紧密中心性
- 7.Betweenness centrality中介中心性
- 8.Katz中心性
- 9.Subgraph centrality(子图中心性)
- 10.Information index
- 二、应用动态过程(如随机游走)和迭代增强( Iterative refinement centralities)方法
- 1.Eigenvector centrality(特征向量中心性)
- 2.Cumulative nomination累积提名方案
- 3.PageRank
- 4.LeaderRank
- 5.HITs
- 6.SALSA
- 三、如何通过观察删除一个节点或一组节点的影响来量化节点的重要性
- 1.Connectivity-sensitive method 对网络连通性的影响
- 2.Stability-sensitive method对网络稳定性的影响
- 3.Eigenvalue-based method 基于特征值的方法
- 4.Node contraction method 节点收缩法
- 四、介绍兼顾具体动力规律和客观动力过程参数的方法。
- 5.Dynamics-sensitive methods 对某些给定动力过程的影响
- 1. Path counting methods 路径计数方法
- 2. Time-aware methods 时间感知方法
- 3. 其他方法
- 五、将从识别单个重要节点转向识别一组重要节点,强调基于物理的方法,如消息传递理论和渗透模型。
- 1.Influence maximization problem(IMP)
- 1. Structural IMP
- 2. Functional IMP
- 3.Heuristic and greedy algorithms 启发式和贪婪算法
- 1. Heuristic algorithms
- 2. Greedy algorithms
- 3.Message passing theory 消息传递理论
- 1.示例一
- 2.示例二
- 4.Percolation methods 渗流方法
- 六、特定类型的网络:在加权网络上 On weighted networks
- 1. Weighted centralities 加权中心
- 1.节点强度
- 2.Weighted coreness 加权核数
- 3.Weighted H-index 加权h指数
- 4.Weighted closeness centrality 加权紧密中心性
- 5. Weighted betweenness centrality 加权中介中心性
- 4. Weighted PageRank and LeaderRank
- 5.D-S evidence theory
- 七、特定类型的网络:On bipartite networks 二部网络
- 1. Reputation systems
- 2. Statistical methods 统计方法
- 3.Iterative methods
- 4.Algorithms with content information 包含内容信息的算法
- 5.Algorithms with user trustiness 基于用户信任度的算法
- 6.Algorithms with the credit of item provider 基于物品提供者信用的算法
- 八、将对代表性方法进行广泛的实证分析,并在不同的网络和目标函数下展示它们的优点、缺点和适用性。
- 1.无向图
- 1.数据集
- 2.结果
- 1.节点与传播影响
- 2.节点对网络连通性的重要性
- 2.有向图
- 1.数据集
- 2.结果
- 3.在加权图
- 1.数据集
- 2.结果
- 4. 在二部图上
- 1.数据集
- 2.结果
- 5.Finding a set of vital nodes 寻找一组重要节点
- 1.数据集
- 九、应用
- 1.识别社交网络中有影响力的传播者
- 2.预测人体必需蛋白质
- 3.量化科学影响 Quantifying scientific influences
- 1.为了提供更精确的测量科学家影响力,一些研究人员借用了**识别关键节点**的概念,**然后通过利用出版物和作者之间的各种关系提出了一些新的度量标准**。
- 2.引文也可以用来衡量科学家的影响力,但不同的引文应该有不同的价值,**这取决于引用的科学家是谁。
- 3.考虑从作者到出版物的引用关系。
- 4.共同作者不同贡献
1.识别与某些结构或功能目标相关的重要节点非常重要
这使我们能够更好地控制流行病的爆发,为电子商务产品进行成功的广告投放,防止电网或互联网的灾难性中断,优化有限资源的使用以促进信息传播,发现药物候选靶点和必需蛋白质,维护通信网络的连通性或为连通性故障设计策略,从专业体育比赛的记录中识别最佳选手,并基于合著和引文网络预测成功的科学家和流行的科学出版物。
2.重要节点的标准多样
有时它需要初始免疫能在流行病传播中最好地保护整个种群的节点,有时它需要损伤将导致最广泛的级联失效的节点,以此类推。
因此,要找到一个最能量化所有情况下节点重要性的通用索引是不可能的。
3.如何在局部索引和全局索引之间,或者在无参数索引和多参数索引之间找到一个很好的折衷是一个挑战。
与基于全局拓扑信息或具有许多可调参数的指标相比,只需要节点局部信息和无参数指标的指标通常更简单,计算复杂度更低,但局部指标和无参数指标的精度通常较差。
4.大多数已知的方法本质上是为识别单个的重要节点而设计的,而不是一组重要节点,而后者更符合实际应用,因为我们经常试图免疫或推送广告给一群人,而不是一个人。
然而,将两个最具影响力的传播者放在一起并不会产生一个具有两个传播者的最具影响力集合,因为两个传播者的影响可能在很大程度上重叠。
事实上,许多启发式算法的思想直接借鉴于个体重要节点的识别,但在识别一组重要节点时表现不佳。
5.为空间网络、时间网络和多层网络等新型网络设计高效有效的方法是该研究领域的新课题。
由于其挑战性和重要意义,重要节点的识别近年来受到越来越多的关注。
识别单个重要节点的方法
基于结构信息
一、结构中心性(Structural centralities)
节点的影响力在很大程度上受其所属网络的拓扑结构的影响和反映。一般来说,中心性度量为网络中的每个节点分配一个真实值,其中产生的值将根据节点的重要性提供一个节点排名。
重要性(中心性)的含义广泛,从不同的方面提出了许多方法。
将结构中心性大致分为基于邻域的中心性 & 基于路径的中心性,并介绍了其中最具代表性的中心性。
-
一个节点的影响力与其影响周围邻居行为的能力高度相关。
(例如,在twitter.com上有影响力的用户有可能直接向更多受众传播新闻或观点。)
因此,一种算法是直接计算节点近邻的数量,即度中心性。 -
度中心性的改进版本,称为LocalRank算法,考虑了每个节点的四阶邻居中包含的信息。
这两种算法都是基于邻域之间的链接数量,而众所周知,局部互联性在信息传播过程中起着负面作用。
-
因此,考虑相邻节点的数量&节点的聚类系数的基础上提出改进新算法。
一般来说,在邻居数量相同的情况下,节点的聚类系数越大,其影响越小。 -
最近,有人认为节点的位置(是否在中心位置)比节点的度更重要。
他们应用了k-core分解,根据节点的残差程度迭代分解网络。
将节点所属的最小核心所对应的最高核心阶数定义为该节点的核心度,认为该核心度是量化节点在传播动态中影响力的更准确的指标。(The highest core order, corresponding to the smallest core a node belongs to, is then defined as this node’s coreness, which is considered as a more accurate index in quantifying a node’s influlence in spreading dynamics.) -
使用著名的h指数来量化用户在社交网络中的影响力。
一个非常有趣的结果是,“度中心性、h指数和核心度” 可以被认为是由离散算子驱动的序列的初始状态、中间状态和稳态。
上述中心性度量实质上是基于节点的邻域,而从信息传播的角度来看,传播速度更快、传播范围更广的节点更为重要,这在很大程度上应受到传播路径的影响。
-
“偏心中心性eccentricity centrality & 紧密中心性 closeness centrality” 都认为一个节点与所有其他节点的距离越短,信息传播越快。
而(1)只考虑到其他节点的所有最短路径之间的最大距离,对少数异常路径的存在非常敏感。
而(2)通过对目标节点与所有其他节点之间的距离进行汇总来消除干扰。 -
节点的中间中心性betweenness centrality定义为网络中经过目标节点的最短路径占所有最短路径的比例。
一般来说,亲密度中心性最小的节点对信息流的视觉效果(?传播效果)最好,而中间度中心性最大的节点对信息流的视觉效果最强。 -
“卡茨中心性Katz” 考虑网络中的所有路径,并对较长的路径分配较少的权重。
-
与Katz中心性类似,子图中心性subgraph centrality计算封闭路径的数量,并对较长的路径给予较少的权重。
-
信息索引The information index还假设信息将在网络中的每一跳中丢失,因此路径越长,丢失的信息越多。
因此,它通过测量从目标节点到所有其他节点的所有可能路径中包含的信息来计算一个节点的影响力。
1.度中心性(基于邻域的中心性)
- 在无向简单网络G(V, E)中,V为节点集,E为链路集,节点vi的 度(ki) 定义为vi的直连邻居数。
- 数学上ki = Σj aij,其中A = {aij}为邻接矩阵,即如果vi和vj连通,则aij = 1,否则为0。
- 度中心性是识别节点影响力的最简单指标:节点的连接越多,该节点的影响力越大。
- 为了比较不同网络中节点的影响,定义归一化度中心度为:

(其中n = |V |是G中的节点数,n -1是可能的最大度数。
上述归一化确实只是为了方便,也就是说,由于网络的组织、功能和密度不同,即使使用归一化度中心性,不同网络中的节点通常也没有可比性。)
1)有时,度中心性表现得出奇地好。
例如,在网络脆弱性研究中,与基于中介性中心性、密切度中心性和特征向量中心性(betweenness centrality, closeness centrality and eigenvector centrality)等更复杂中心性的选择攻击方法相比,度目标攻击可以非常有效地破坏无标度网络和指数网络(scale-free networks and exponential networks)。
2)此外,当扩散率非常小时,度中心性是一个比特征向量中心性(eigenvector centrality)和其他一些众所周知的中心性更好的识别节点扩散影响的指标。
在有向网络D(V, E)中,每个链路都与一个方向相关联,那么我们要分别考虑节点的出度和入度。
例如,考虑twitter.com,节点vj到节点vi之间存在有向链接,如果vj紧随vi,那么节点vi的入度(即指向vi的有向链接的节点数量)反映了vi的受欢迎程度,而vi的出度(即从vi到其他节点的链接数量)在一定程度上代表了vi的社交活动。
3)在加权网络中,度中心性通常被强度所取代,强度定义为相关链接的权重之和。
2.四阶邻居信息(基于邻域的中心性)
度中心性在评价节点影响时可能不太准确,因为它使用的信息非常有限。
作为程度中心性的扩展,Chen等人提出了一种有效的基于局部信息的算法LocalRank,该算法充分考虑了每个节点的四阶邻居所包含的信息。
节点vi的LocalRank评分定义为:
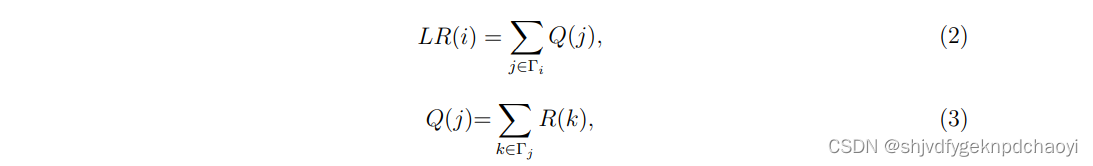
(Ti是vi的邻居集合,R(k) 是vk的一阶和二阶邻居)
LocalRank算法的时间复杂度比典型的基于路径的中心算法低得多。
事实上,LocalRank算法的计算复杂度几乎随网络规模线性增长。
LocalRank算法也可以扩展为加权网络。
3.ClusterRank(基于邻域的中心性)
局部聚类(局部互联性)通常在传播过程中起消极作用,以及在演化网络的增长中起消极作用。
与度中心性和LocalRank算法不同,ClusterRank不仅考虑最近邻居的数量,还考虑了它们之间的交互。
ClusterRank定义在有向网络中,其中从vi到vj的链接记为(i→j),意味着信息或疾病将从vi传播到vj。
- 节点vi的ClusterRank评分定义为:
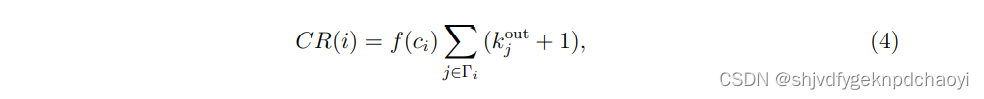
- 其中f(ci)是有向网络D中节点vi的聚类系数ci的函数,定义为:
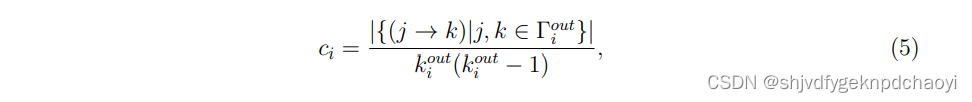
(k是出入度,T是邻居集合。) - 由于局部聚类起负作用,因此f(ci)应该与ci负相关,例如:

4.Coreness(基于邻域的中心性)
从相关的角度来看,对于信息在多个社区的网络中传播的情况,信息一旦到达一个社区,就会迅速地在本地传播。
连接多个社区的节点将具有在全球范围内传播信息的潜力。
因此,通过计算节点连接的社区数量 来计算节点的影响力。
同样,组间跨结构孔(structural holes)的节点更有可能表达有价值的想法,具有更高的影响力,因此提出了考虑结构孔的排序算法。
- 度中心性只考虑最近邻居的数量,并断言具有相同度的节点在网络中具有相同的影响力。
Kitsak等人认为,在评估节点的传播影响力时,节点的位置比它的近邻更重要。
也就是说,如果一个节点位于网络的核心部分,那么该节点的影响力将高于位于外围的节点。 - 因此,Kitsak等提出了核度作为节点传播影响力更好的指标,该指标可通过网络中的k-core(也称为k-shell)分解得到。
1)给定无向简单网络G,初始定义每个孤立节点vi(即度ki = 0)的核度(coreness) ci为ci = 0,并在k核分解前去除这些节点。
2)然后在k-核分解的第一步中,去除k = 1次的所有节点。
这将导致剩余节点的度值减少。
3)连续去除剩余度k≤1的所有节点,直到剩余节点剩余度k > 1为止。
4)在第一步分解中从1壳层中移除的所有节点及其核数ks都等于1。
5)在第二步中,所有度数k = 2的剩余节点将首先被删除。
6)然后迭代去除剩余度k≤2的所有节点,直到剩余度k > 2的所有节点。
7)第二步分解中从2-壳层中去除的节点及其核ks为2。
分解过程将继续进行,直到所有节点都被删除。
8)最后,节点vi的核数等于其对应的壳层。
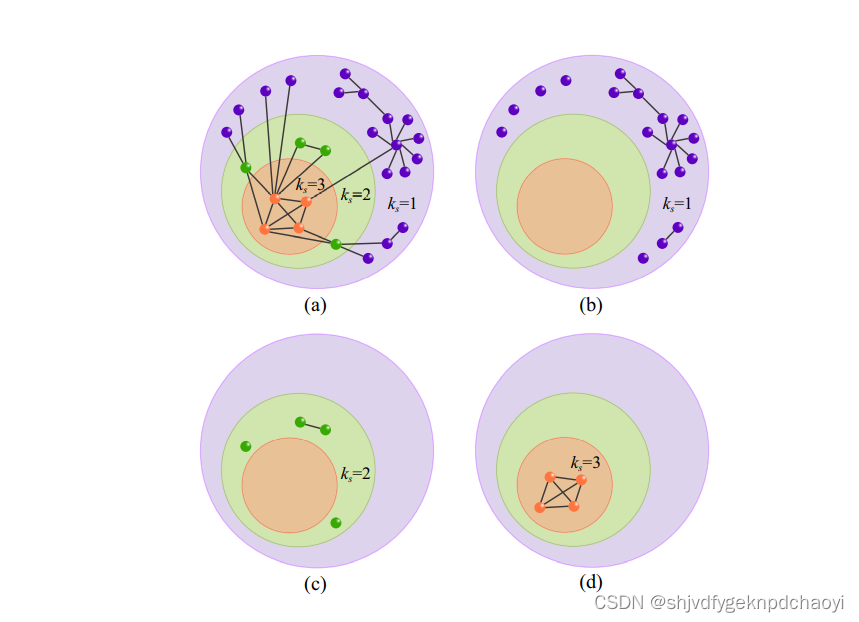
图1是k-核分解的简单示意图。
显然,具有更大核心度的节点意味着该节点位于更中心的位置,并且可能在网络中更重要。
- 考虑连接到被移除节点的链路数,表示为耗尽度k,节点vi的混合度定义为:
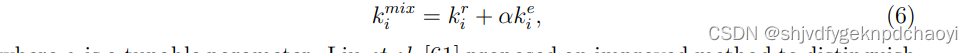
(其中α是一个可调参数。)
Liu等提出了一种改进的方法来区分同层节点的影响。通过测量目标节点到网络核心中所有节点的最短距离之和,即核数最高的节点集。
Hu等人[62]结合了网络的k-core和社区属性,提出了一种新的模型。
Luo等人[63]认为在k-core分解中应将弱联系和强联系分开考虑。
Min等人[64]提出了一种基于对人类行为和社会机制调查的算法。
Pei等人[59]发现,在不同的社交平台上,重要节点一致位于k核。
Borge-Holthoefer和Moreno[65]研究了谣言动力学中的k核分解。
Liu等人[66]提出了一种新颖有效的方法,首先去除冗余链接,然后应用常规的k核分解。
5.H-index(基于邻域的中心性)
迭代k核分解过程需要网络的全局拓扑信息,这限制了它在非常大规模的动态网络上的应用。
与核心度不同,h指数(赫希指数)是一种局部中心性,其中每个节点只需要少量的信息,即相邻节点的度。
- 节点vi至少有h个度不小于h的邻居。
数学上,我们可以在有限个实数变量{x1, x2,···,xm}上定义一个算子H,它返回最大整数H,使得在{x1, x2,···,xm}中至少有H个元素的值不小于H。据此,社交网络中节点vi的H指数可以写成:
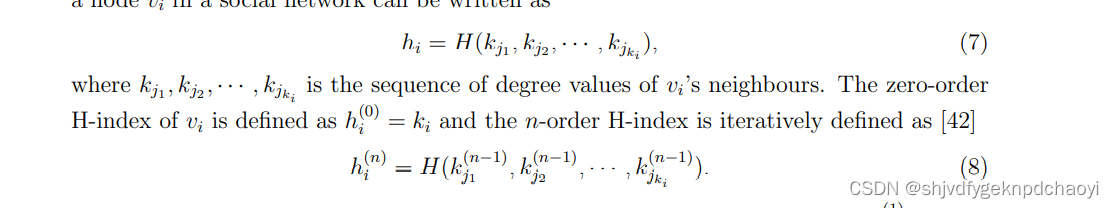
(0)零阶,(n-1)阶,迭代获得。 - vi的经典h指数等于一阶h指数,即h(1) i
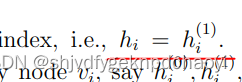
证明了在有限步长之后,每个节点vi的h指数h(0) i, h(1) i, h(2),···i将收敛到其核心(coreness),即:
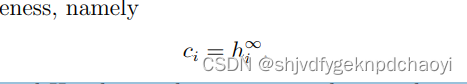
- 因此,度、经典H指数(一阶)和核心度(H指数有限步长收敛后得到)是由算子H驱动的初始状态、中间状态和稳态。
其他所有H指数(顺序不同)也可以用来衡量节点的重要性。
h指数可以很容易地扩展到有向网络和加权网络,其中节点的度数可以用节点的入度数、出度数或节点强度代替。
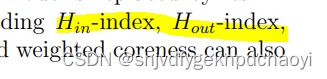
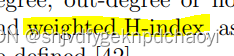
同理,coreness核心度也可以扩展为:in-coreness, out-coreness, and weighted coreness
6.Eccentricity离心率(基于路径中心)
- 在已连接的网络中,定义dij为节点vi到vj之间的最短路径长度。
我们认为,节点vi与所有其他节点的距离越短,该节点越中心。
因此,节点vi的偏心量定义为到其他节点的所有最短路径之间的最大距离:
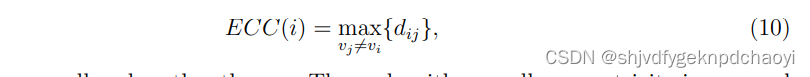
(其中vj表示除vi之外的所有节点) - 偏心率越小的节点影响越大。为了比较不同网络的偏心率,vi的归一化偏心率定义为:

最大距离可能会受到一些异常长的路径的影响,那么偏心率可能不能反映节点的重要性(见图3中的一个例子)。
6.Closeness centrality紧密中心性
而紧密中心性通过汇总目标节点与所有其他节点之间的所有距离来消除干扰。
- 对于一个连通的网络,节点vi的紧密中心性定义为vi到所有其他节点的平均测地线距离的倒数:
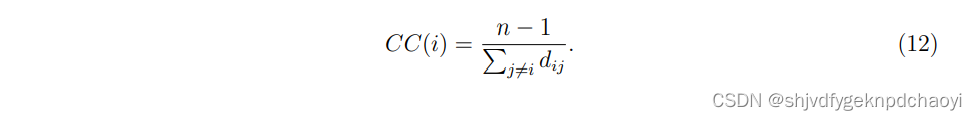 距离越大,节点越中心。
距离越大,节点越中心。
接近中心性也可以理解为信息在网络中的平均传播长度的倒数。
一般来说,接近度值最高的节点对信息流具有最佳的洞察力。
不幸的是,原始的定义有一个主要的缺点:当网络不连通时(在有向网络中,网络必须是强连通的),存在一些dij =∞的节点对。 - 因此,一种非常流行的方法是根据节点之间的谐波平均距离的倒数来计算亲密中心性:

- 节点的紧密中心性反映了它与其他节点交换信息的效率。受此启发,网络效率被定义为网络中节点的平均效率G:
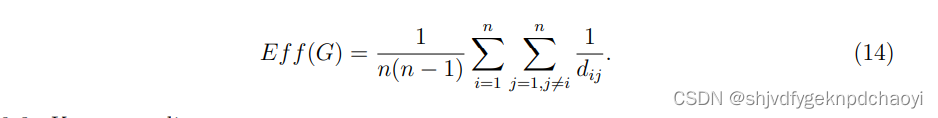
7.Betweenness centrality中介中心性
- 通常,从节点vs开始,到vt结束的最短路径不止一条。
通过计算经过vi的所有最短路径,可以计算出vi的信息流的可控性。
因此,节点vi的中介中心性可定义为:

(其中gst是vs到vt的最短路径的个数,gst^i是vs到vt的所有最短路径中经过vi的路径的个数。)
- 考虑有n个节点的星型网络的两个极端情况。
显然,叶节点不在任何最短路径上,因此根据式(20),它的中介中心性等于0,而对于星形的中心节点,在另一种极端情况下,它的中介中心性等于(n−1)(n−2)/2,这是中介中心性可能的最大值。
因此,无向网络中节点vi的归一化介心中心性为:
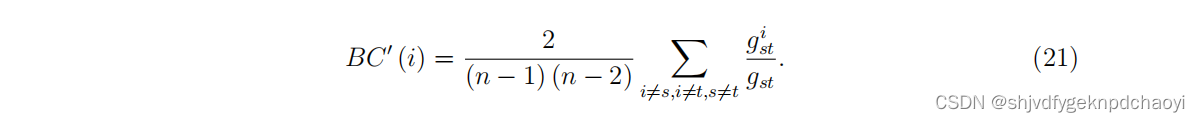
为了便于计算,研究人员还采用了近似归一化形式的介数,例如:
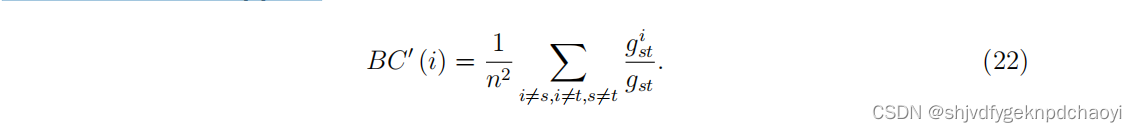
- Goh等人研究了无标度网络(各节点之间的连接状况(度数)具有严重的不均匀分布性:网络中少数称之为Hub点的节点拥有极其多的连接,而大多数节点只有很少量的连接。) 中所有数据包都经过最短路径的数据包传输。
如果一个给定的节点对之间有多个最短路径,数据包将遇到分支点,并将均匀地分布到这些路径上。
实际上,节点vi的中介中心性相当于每个节点向每个节点发送一个数据包时,在vi处的负载,忽略数据包的干扰和延迟。
Goh等发现介数中心的分布遵循幂律,这对无向和有向无标度网络都是有效的。
-
提出了一种组间中心性来度量一组节点的中心性,即通过该组中至少一个节点的最短路径。
Kolaczyk等人进一步讨论了群间中心性和共间中心性的关系,通过通过群中所有节点的最短路径来计算一组节点的中心性。
然而,许多因素,如负载平衡和容错,可能导致一些折衷策略,其中数据包并不总是通过真实商业传输网络中的最短路径传递。 -
也有研究表明,在所有节点对之间选择最短路径可能会导致交通拥堵问题。
Freeman等人提出了一种称为流中介中心性的算法,该算法考虑了给定节点对之间的所有路径。
在数学上,vi的流中介中心性定义为:
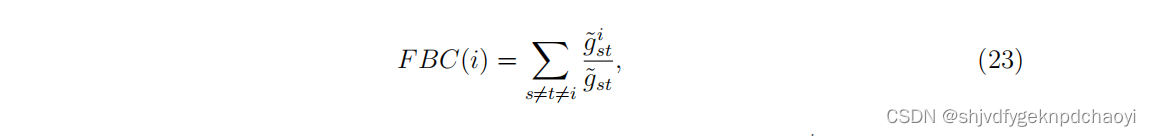
( ̄gst是从vs开始、结束于vt的最大流量,而 ̄g I st是从vs开始、结束于vt通过vi的流量。)
在最大流量问题中,s-t切割是将节点vs和vt分成两个互不相连的分量的划分。
割集容量(?)是组成割集的各个环节容量的总和。
著名的min-cut, max-flow定理证明了从vs到vt的最大流量恰好等于最小切割容量
- 可通信性中介中心性(Communicability betweenness centrality) 还通过引入缩放将所有路径都考虑在内,使较长的路径承载较少的贡献
如果Wst^§是连接节点vs和vt的长度为p的路径数,它们之间的可通信性可定义为:

(其中A是邻接矩阵。)
则无向网络中节点vi的可通信介心中心性为:
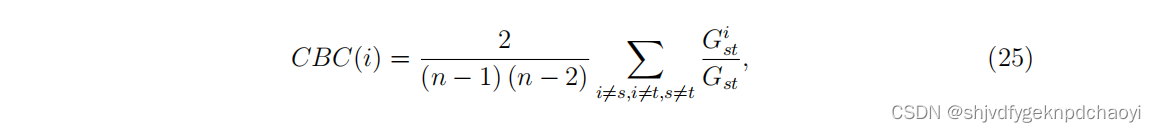
其中Gst^i是vs和vt之间对应的可通信性,其中涉及节点vi。
讨论了可通信性中介中心性的上下限。
- 随机游走中间中心性(Random-walk betweenness centrality) 是另一种著名的中间性变体,它计算网络中的所有路径,并赋予较短路径更多的权重
顾名思义,该算法计算任意对节点之间的随机行走中一个节点被遍历的预期次数。
节点vi的随机游走中介中心性可表示为:
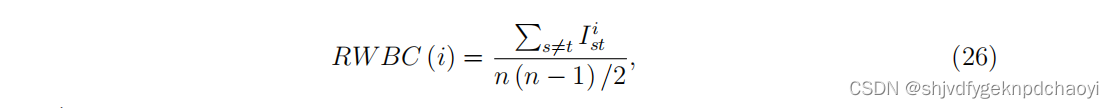
(Ist^i是vi中从vs开始到vt结束的行走次数。) 详细计算参考文献。
为了计算Ist^i,我们首先构造网络的拉普拉斯矩阵为:

8.Katz中心性
与只考虑节点对之间最短路径长度的紧密中心性不同,Katz中心性通过考虑网络中的所有路径来计算节点的影响。
- 卡茨中心性认为较短的路径起着更重要的作用。
- 假设节点vi和vj之间的路径长度dij = p,则路径对节点vi和vj的重要性的贡献为s^p,其中s∈(0,1)是一个可调参数。
显然,如果s很小时,较长的路径的贡献将被很大程度地抑制。
假设lpij是vi和vj之间长度为p的路径数,我们有(lpij) = A^p,其中A是网络的邻接矩阵。
因此,可得描述任意对节点之间关系的交互矩阵为:
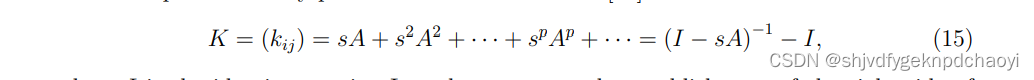 I是单位矩阵。
I是单位矩阵。
为了保证式(15)右侧的建立,s必须小于a的最大特征值的倒数。kij的值在网络科学中也称为节点vi和vj之间的Katz相似度。
节点vi的Katz中心性定义为:
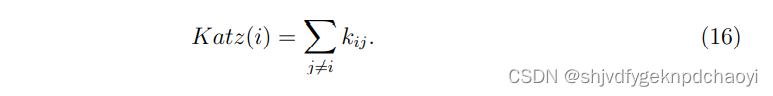
卡茨中心性计算复杂度高,难以应用于大规模网络中。
9.Subgraph centrality(子图中心性)
节点vi的子图中心性定义为从vi开始到结束的所有封闭路径数的加权和。
与紧密中心性和信息索引相似,长度越短的路径对相关节点的重要性贡献越大。
长度为p,从vi开始到vi结束的封闭路径的个数,可由邻接矩阵的第p次幂的第i个对角元素,即(Ap)ii得到。
- 事实上,当p = 1时(A^1)ii = 0, 当p = 2时(A^2)ii = ki
定义节点vi的子图中心性为:
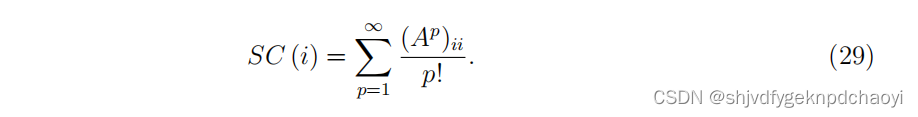
- 如果网络是n个节点的简单网络,则节点vi的子图中心性可计算为:
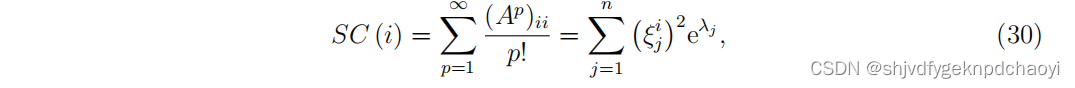
( λj 是 A的特征值,ξ j是特征向量) - 但是,如果网络是一个n > 1的简单连通网络,则节点vi的子图中心性满足不等式:
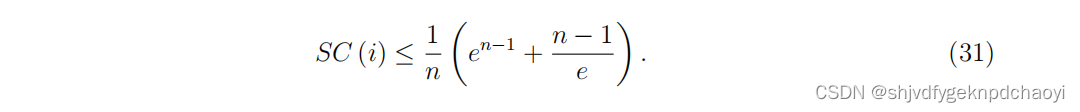
等式成立当且仅当网络是完整的。
子图中心性在寻找更重要节点方面具有良好的性能,也可用于检测网络中的motif。
10.Information index
- 信息中心性指数(也称为S-Z中心性指数)根据网络中节点对之间所有可能路径所包含的信息来衡量节点的重要性。
- 假设每个环节都存在噪声,在信息的每一次转换过程中都有损耗。路径越长,损失越大。
- 从数学上讲,在一条路径上传输的信息总量等于路径长度的倒数。
- 一对节点vi和vj之间可以传输的信息量等于它们之间通过每一条可能路径传输的信息的总和,记为qij。
- 信息索引考虑连接网络中所有可能的路径,但不需要枚举它们。
事实上,qij已经被证明等价于电网中的电导[70,71]。
根据电网络( electrical network theory)理论,可以得到vi和vj之间的信息总量为:
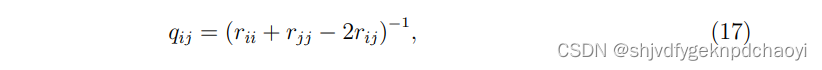
(rij是矩阵中的一个元素)
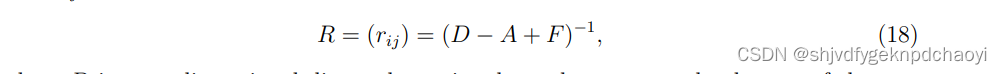
其中D是一个n维对角矩阵,它的元素是四个响应节点的度,F是一个n维矩阵,它的元素都等于1。
然后将vi的信息指数定义为qij的谐波平均值:
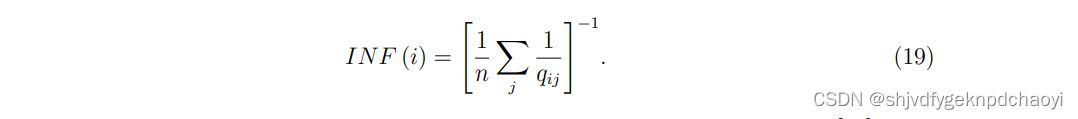
二、应用动态过程(如随机游走)和迭代增强( Iterative refinement centralities)方法
节点的影响不仅取决于其邻居的数量,还取决于邻居的影响,称为相互增强效应。在本章中,我们将选择一些典型的操作细化中心,其中每个节点都得到其邻居的支持。
-
eigenvector centrality(特征向量中心性)& cumulative nomination algorithm(累积提名算法)设计在无向网络中。
-
而PageRank、HIT及其变体主要用于有向网络中。
-
PageRank最初用于对网页进行排名,是谷歌搜索引擎的核心算法。
为了解决悬空节点问题,PageRank引入了一个随机跳跃因子,它是一个可调参数,其最佳值取决于网络结构和目标函数。 -
LeaderRank通过添加通过双向链路连接到每个节点的接地节点,与2n个链路相关联的接地节点使网络强连接,并消除所有悬空节点。
然后,使用随机行走的所有节点上的访问概率的稳定分布来量化节点的重要性。 -
由于节点在定向网络中可能扮演不同的角色,HITs算法从两个方面评估每个节点:权威和中枢。
在有向网络中,节点的权限分数等于指向该节点的所有节点的中心分数的总和,而节点的中心得分等于该节点指向的所有节点权限分数的总和。
1.Eigenvector centrality(特征向量中心性)
- 特征向量中心性假设,节点的影响不仅取决于其邻居的数量,而且取决于每个邻居的影响。
节点的中心性与其所连接节点的中心度之和成比例。用xi表示的节点vi的重要性:

其可以矩阵形式写成:

1)其中c是比例常数。通常,c=1/λ,其中λ是A的最大特征值。通过幂迭代方法可以有效地计算特征向量中心性。
2)在幂迭代开始时,每个节点的分数被初始化为1。然后每个节点将其分数平均分配给其连接的邻居,并在每一轮迭代中接收新值。
3)重复此过程,直到节点的值达到稳定状态。
从这种迭代方法的观点来看,PageRank算法是特征向量中心性的变体。
在一般情况下,特征向量中心性得分更倾向于集中在几个节点上,这使得很难在节点之间进行区分。
- Martin等人基于无向网络的Hashimoto或非回溯矩阵的前导特征向量,提出了一种改进的特征向量中心性,称为非回溯中心性
非回溯中心性的主要思想是:当计算节点vi的中心性得分时,vi的邻居在求和中的值将不再考虑vi的影响。
- 然而,在有向网络中,许多节点通常只有out度,导致在第一轮功率迭代之后处于零状态。为了解决这个问题,Bonacich等人提出了一种特征向量中心性的变体,称为阿尔法中心性:
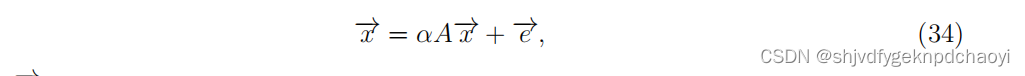
(e是( vector of the exogenous sources of status)状态的外生来源的向量,α是反映内生因素与外生因素相对重要性的参数。若假设e是一个1的向量,得到了与Katz中心性基本相同的解。)
2.Cumulative nomination累积提名方案
特征向量中心性可能并不总是一种理想的方法,因为它的收敛速度很慢,有时会陷入无休止的循环。
累积提名方案假设更多的中心个体在社交网络中会更频繁地被提名,
并考虑每个节点及其邻近节点的指定值。
-
开始,每个节点的提名值初始设置为1。然后每个节点都得到提名,更新后的值等于它的原始值加上和在每次迭代中邻居的值。 当所有节点的归一化累积提名达到稳态时,提名迭代停止。
t次迭代i后指定节点vi的累积:
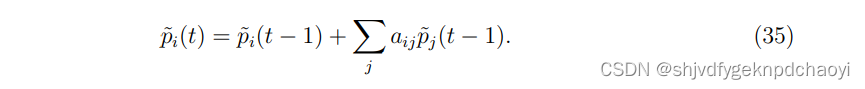
(pi(t−1)表示节点vi经过t−1次迭代后的累计提名数。) -
vi的归一化累积命名可计算为:
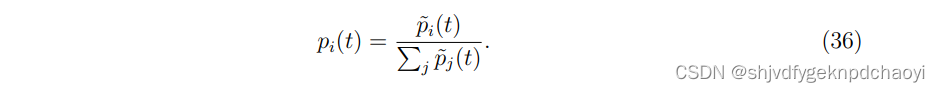
累积提名与阿尔法中心性公式相似。
虽然不同之处在于,alpha中心性中的向量e是一个固定的向量,但是,累积命名中的对应元素,例如pi(t),等于最后迭代中的节点的值,这提高了收敛速度。
3.PageRank
PageRank算法是特征向量中心性的一个著名变体,并被用于在谷歌搜索引擎和其他商业场景中为网站排名。
传统的基于关键词的网站排名算法容易受到恶意攻击,通过增加不相关关键词的密度来提高网站的影响力。
PageRank通过在网络上随机行走,从网页的关系构建来区分不同网站的重要性。
类似于特征向量中心性,PageRank假设一个网页的重要性是由数量和链接到它的页面质量。
- 最初,每个节点(即页面)获得一个单位PR值。
然后每个节点将PR值均匀地分配给它的出站链路上的邻居。
数学上,节点vi在t步处的PR值为:
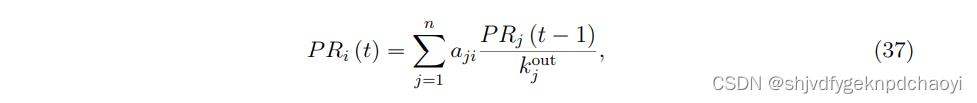
(n为网络中节点总数,kj^out为节点vj的出度。)
如果所有节点的PR值都达到稳态,则上述迭代停止。
上述随机游走过程的一个主要缺点是悬空节点(出度为零的节点)的PR值不能重新分配,那么Eq.(37)不能保证收敛.
- 对于这些问题,我们引入了一个随机跳跃因子,假设浏览者会以s的概率沿着链接浏览网页,并以1−s的概率离开当前页面,打开一个随机页面。 因此,将式(37)修改为:
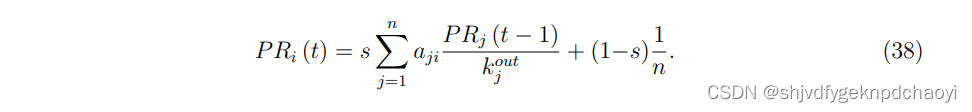
当s = 1时,式(38)返回到式(37)。
随机跳跃概率s通常设置在0.85左右,但确实应该在不同的场景中进行测试。
它已被应用于通过网络结构对广泛的对象进行排名:
对图像和书籍进行排序,对生物学和生物信息学中的基因和蛋白质进行排序,对化学中的分子进行排序,对Neu科学中的脑区和神经元进行排序,对复杂信息系统中的主机名、Lonux内核和编程接口进行排序,对社会网络中的领导人进行排序,对文献计量学中的科学家、论文和期刊进行排序,对运动员和运动队进行排名。
研究了用PageRank评估节点的传播能力时,在扰动网络(perturbed networks)中超稳定节点(super-stable nodes)的出现。
他们调查了不同拓扑属性的排名,发现PageRank在随机网络中对摄动很敏感,而在无标度网络中是稳定的。
4.LeaderRank
PageRank中每个节点的随机跳转概率是相同的,这意味着一个浏览者从一个有信息的网页和从一个琐碎的网页离开的概率是相同的,这与实际情况不相符。
此外,如何确定参数,以达到最佳的排名取决于具体的场景。
- LeaderRank提供了一个简单而有效的解决方案,通过添加一个接地节点,通过n个双向链接连接到所有其他节点。
因此,该网络是强连接(如果有向图G的任何两顶点都互相可达,则称图G是强连通图)的,由n + 1个节点和m + 2n个有向链路组成。
1)最初,除地面节点外,每个节点分配一个单位分数。
2)每个节点沿着出站链路平均地将其评分分配给相邻节点。
3)当所有节点的分数达到稳定状态后,地线节点的值将被均匀分配到所有其他节点。
节点vi在时间步t阶段i处的值:
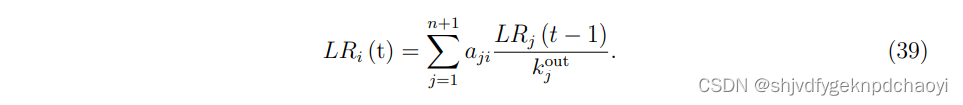
节点vi的最终得分为:
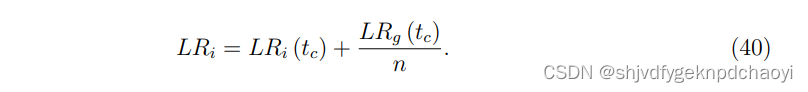
该自适应无参数算法对在线社交网络具有很好的性能。
大量的实验表明,由于网络是强连接的,且直径仅为2,因此LeaderRank收敛速度更快。
就排名有效性以及对操纵和噪声数据的鲁棒性而言,LeaderRank优于PageRank。
同样的想法,即增加一个地面节点,也被证明可以有效解决推荐系统的准确性-多样性困境。
- 进一步改进了LeaderRank算法,允许popular节点在随机漫步中从地面节点获得更多的值。
对于入度为ki ^in的节点vi,从接地节点到vi的链路权值为wgi = (ki ^in) ^α,其中α为自由参数。
其他环节的权重保持不变。
因此,改进后的LeaderRank在时间步t处vi的得分为:

5.HITs
HITs算法考虑了每个节点在网络中的两个角色,即authorities和hubs。
在万维网中,权威网站总是可靠的,提供特定主题的原始信息,而枢纽hub网站是那些链接到许多相关权威的网站。
枢纽和权威表现出一种相互强化的关系:一个好的枢纽指向许多权威,而一个好的权威则被许多枢纽指向。
在有向网络中,一个节点的authority评分等于指向该节点的所有节点的hub评分的总和,而一个节点的hub评分等于该节点指向的所有节点的authority评分的总和。
在n个节点的网络中,分别用ai(t)和hi(t)表示节点vi在t时刻的authority评分和hub评分。
首先,将所有节点的hub分数分配为1。
数学上,节点vi在t时刻的authority和hub值分别为:
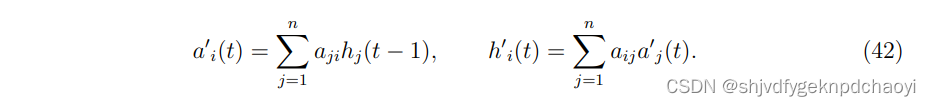
每次迭代后,每个节点的分数应归一化为:
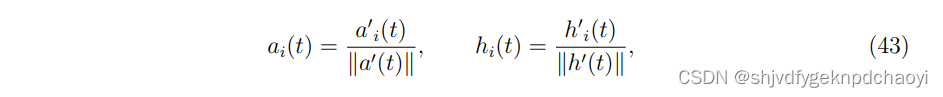
如果所有节点的归一化分数都达到稳态,迭代就会停止。
HITs算法是收敛的。
6.SALSA
SALSA是用于链路结构分析的随机方法的简称,是HITs算法的一个著名变体,它建立在有向网络上随机行走的随机特性基础上。
-
SALSA的第一步是将有向网络映射到二部无向网络(设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。)
-
出度非零的节点构成hub集(即SH),入度非零的节点构成authority集(即SA)。
如果hub节点vih通过原有向网络指向authority节点via,则两个节点将在二部网络中连接。
图4给出了该映射过程的一个示例。

一个由有向网络构建二部无向网络的例子,其中在二部表示中,孤立的节点被去除。
假设原网络上随机行走的每一步都由对应的二部网络中的两条相邻边组成,且这两条边必然从不同的边出发。
每条长度为2的路径都表示在适当的方向上穿过一个链接(从hub端到auth端),并沿链接后退。
例如,图4中的路径{(v2h, v3a),(v3a, v4h)}表示从v2到v3的有向链接的遍历和沿着从v4到v3的链接的后退。
- 在初始阶段,将hub-side节点的值赋为1,用h(0)表示,因此计算t时刻hub-side节点的值为:
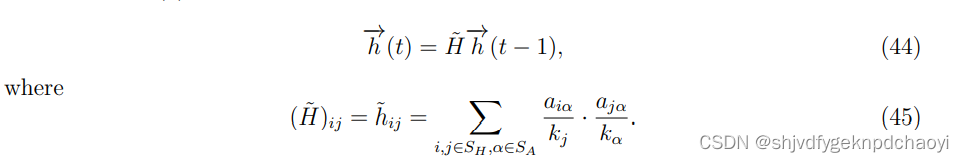
- 同样,authorities的值可以通过从authority-side开始的随机游走得到:
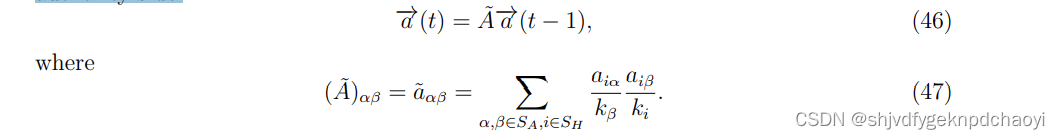
注意,用于计算hub和authority分数的两个随机漫步是相互独立的,这与两个值相互增强的HITs有很大不同。
然而,SALSA和HITs都使用相同的元算法,而且SALSA相当于对网络的链路结构进行加权的度内分析,这使得它在计算上比HITs更高效。
三、如何通过观察删除一个节点或一组节点的影响来量化节点的重要性
-
以上方法都没有考虑到目标函数中所涉及的动力过程的特征。
无标度网络(无标度网络具有严重的异质性,其各节点之间的连接状况(度数)具有严重的不均匀分布性)在随机故障面前是稳定的,但在蓄意攻击下是脆弱的,这意味着有些节点在保持网络连通性方面更重要。 -
如果一个节点(或一组节点)被移除会大大缩小巨大的组件,那么它就很重要。
通过节点移除和收缩方法找到一组节点与系统科学中确定系统核心的思想相一致。
系统的核心被定义为一组节点,这些节点的重要性可以通过移除后出现的连接组件的数量来简单量化。 -
然而,不同的连接组件可能有不同数量的节点和不同的功能。
如果删除一个节点(或一组节点)会大大降低网络的稳定性或鲁棒性,或使网络更脆弱,则认为该节点是重要的。 -
许多基于路径的方法被提出来度量脆弱性。
例如,一个鲁棒网络在节点之间应该有更多的不相交路径(如果没有共同的中间节点,两条路径就是不相交的)。
Dangalchev评估去除节点后的平均紧密度中心性,称为剩余紧密度,以衡量网络的脆弱性。
另外,Chen等采用网络生成树的数量来衡量通信网络的可靠性,认为越可靠的网络往往拥有越多的生成树。 -
此外,节点的去除也会影响网络上的动力学过程。
因此,节点的重要性也可以通过网络邻接矩阵最大特征值的变化来衡量。 -
节点上的另一种操作是将节点及其邻居压缩为新节点,命名节点收缩方法。
收缩一个节点后,如果整个网络变得更加聚集,则认为该节点更重要。
例如,星型网络将在收缩中心节点后收缩到单个节点。
下面,根据对节点的不同操作类型和考虑的目标函数的不同,我们将所有这些方法分为四类。
1.Connectivity-sensitive method 对网络连通性的影响
-
如前所述,我们可以从三个方面来衡量节点移除后对网络连通性的破坏,即巨型组件的大小、连接组件的数量和节点之间的最短距离。
前两个非常直观。对于最短距离,直接计算网络工程平均最短距离的变化是不够准确的。 -
特别是,网络连通性的丧失来自三种情况:
(i)被删除的节点集与剩余的节点之间的断开连接;
(ii)被移除节点之间的断开;
(iii)节点移除后剩余节点之间的断开。
前两种被认为是网络连接的直接损失,而第三种被认为是间接损失。 -
一个基本假设是,直接损耗和短距离连接比间接损耗和长距离连接更具破坏性。
两个节点之间连通性的损失可以用距离的倒数来量化。
在删除一个节点(比如vi)之后,假设出现了一些不相交的节点对,用集合E表示(包括直接和间接损失)。
vi的重要性可以定义为:

(djk为节点vj到vk在去除vi之前的距离。
当j = i或k = i时,DSP(i)为直接损失;
j ≠ k ≠ i 时为间接损失。)
这个公式很简单,但如果只删除一个节点,通常是无效的,因为仅删除一个节点不太可能将现实世界中的大型网络分解成碎片。
在这种情况下,间接损失为0,DSP退化为被移除节点到所有其他节点之间距离的倒数和,相当于接近中心性closeness centrality。
2.Stability-sensitive method对网络稳定性的影响
虽然移除一个节点不太可能摧毁真实的网络,但它确实会影响网络的稳定性或脆弱性。
在通信网络中可以找到一个强有力的证据,删除一个重要节点可能不会导致传输消息失败,但很可能会延迟传输,甚至导致信息阻塞。
从网络结构的角度出发,有一些衡量网络稳定性或脆弱性的指标。
-
其中,节点之间的最短距离是应用最多的。
例如,紧密中心性 the closeness centrality可以被认为是通信网络中信息传播长度的度量。
如果一个网络的紧密度(即所有节点的紧密度之和)很高,那么通过这个网络的传输就会非常有效。可以用来衡量节点的重要性。
也就是说,如果一个节点被移除会使网络更脆弱,那么它就会被认为更重要。 -
接下来,我们提出了一些基于节点移除策略的网络脆弱性度量的相关方法。
剩余紧密中心性 the residual closeness是紧密中心性的变体。
引入指数函数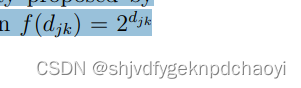 来重新定义节点vi的接近度,为:
来重新定义节点vi的接近度,为:
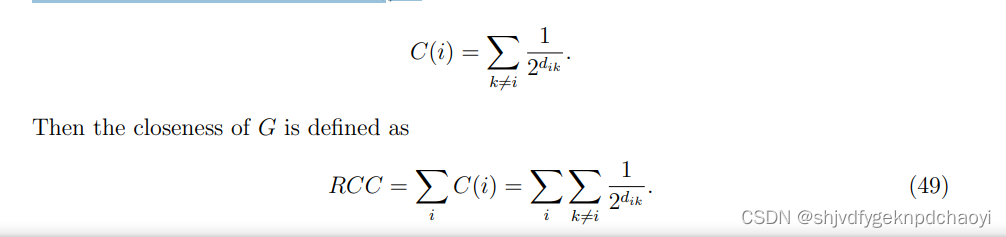
对于具有n个节点的星形图,RCC=(n−1)/2+(n− 1) (1/ 2+(n−2)/4)=(n−1)(n+2)/4
而对于具有n个节点的链,RCC=2n− 4+(1/2^(n−2))删除节点后,网络的脆弱性将发生变化,这可以由RCC(i)捕获,即删除vi后剩余网络G{vi}的RCC。
然后,可以通过the residual closeness 剩余封闭度R=mini { RCC(i)}获得网络的脆弱度。 -
根据这一思路,即采用去节点后网络脆弱性的变化来衡量节点的重要性,也有研究从其他方面对脆弱性进行了量化。
例如,Rao等人认为,在没有有效的最短路径之前,信息不会沿着较长的路径传播。
因此,他们认为脆弱性可以通过节点之间最短路径的数量来衡量。
1)用平均等效最短路径(yij = xij/µ)来衡量差异。
(Xij为现实网络中vi和vj之间最短路径的个数,最短路径的长度为dij,而µ为对应的全连通网络中2)两个节点之间长度不大于dij的最短路径的个数。)
3)然后用整个网络的yij的平均值来计算网络的脆弱性
-
除了最短路径,Bao认为不相交路径的数量也可以衡量网络的脆弱性。
如果两条路径没有共享任何节点,则两条路径是不相交的。
因此,与基于最短路径的方法不同,该方法认为节点间通道的多样性对度量节点间可达性的脆弱性更为重要。
与基于等效路径的方法类似,该方法也以全连接网络为基准。
定义节点vi和vj之间的脆弱性为V (vi, vj) = Pij/Pij^full,且 i ≠ j
(其中Pij为vi和vj之间的不相交路径数,Pij^full为对应的全连接网络中不相交路径数。)
然后通过V (G) = Σ Pij/ Σ Pij ^ full计算网络的脆弱性。 -
此外,Chen等人认为,如果一个节点被移除,它导致"生成树数量较少的子图",就更重要。
一个连通良好的图通常有多个生成树,而一个不连通的图没有。即网络的稳定性与生成树的个数有关。
无向图G的生成树是一个子图它包含了G的所有节点。生成树的数目可以用拉普拉斯矩阵L = D−A来计算。
生成树的数量t0可以用t来计算: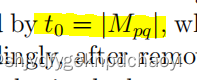
(其中Mpq是对应于L中的任意项lpq的子项。)
因此,去掉vi后,可以得到剩余网络的生成树数,记为tG{vi}。
然后通过下式计算节点的重要性。

与连接性敏感的方法相比,本小节中描述的方法对仅删除一个节点更敏感。
但当网络非常脆弱时,即使随机删除一个节点也会使网络破碎,稳定性敏感方法的优势将不再明显。
特别是基于生成树的方法,如果节点删除导致组件断开,则会失败。
3.Eigenvalue-based method 基于特征值的方法
网络上的许多动态过程是由网络邻接矩阵A的最大特征值(λ记录的)决定的。
因此,λ在去除一个节点(或一组节点)后的相对变化可以反映该节点(或一组节点)对动力学过程的影响。
具体来说,节点移除引起的变化越大,被移除的节点就越重要。
-
Restrepo等人利用这一原理来测量节点(和边)的动态重要性。
u和v分别表示A的左右特征向量,则Au = λu和v^T(转置)且v ^T A = λv ^T
节点vk的动态重要性,与差量−∆λk(λ在去除vk后减少)成正比,记为:
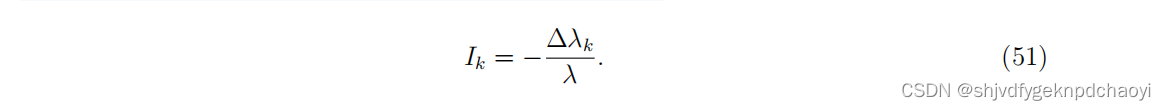
使用近似计算:

-
该方法既可以应用于有向网络,也可以应用于加权网络
也用来衡量一个边的动态重要性,但有一个不同的公式:
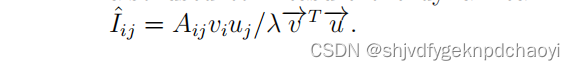
4.Node contraction method 节点收缩法
- 节点收缩曾被应用于复杂网络的粗粒度分析,它将一个节点及其邻居节点收缩为一个新节点。
如果一个节点是非常重要的核心节点,收缩该节点后,整个网络会更加聚集。
该方法的关键是量化网络的聚集程度,聚集程度由节点数n和平均最短距离d决定。
如果一个网络同时具有较小的n和d,则该网络具有较高的集聚度。
这从社会学的角度很容易理解:如果一个社会网络的人更少(小n),成员之间可以方便地交流(小d),那么这个社会网络就更聚集。
则定义网络G的聚集度为:
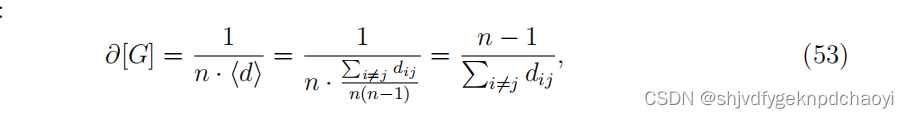
(dij是vi和vj之间的距离。
当n = 1时,∂[G]设为1。
那么0 <∂[G]≤1。)
节点的重要性可以由∂[G]在收缩节点后的变化来反映,定义为:
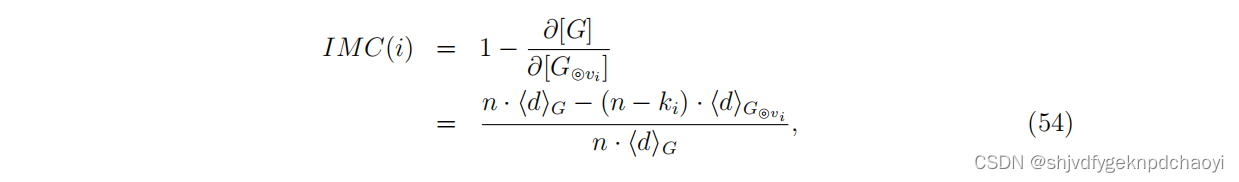
(∂[G} vi]是收缩节点vi后网络的凝聚度,G表示G的所有节点之间的平均距离,ki是节点vi的度数。)
1)显然,IMC(i)是由vi的邻居数量和vi在G中的位置共同决定的。如果ki较大,vi的收缩会大大减少G中的节点数量,说明度越大的节点往往越重要。
2)同时,如果vi经过多条最短路径,则vi的收缩会大大缩短G的平均距离,导致节点vi的IMC增大。
3)因此可以看出,这个度量同时体现了度中心性和中介中心性的思想。
然而,节点收缩法不能应用于大规模网络,因为计算每个节点的平均距离 Gvi (i = 1,2,···,n)非常耗时。
-
Wang等人利用节点收缩方法引入链接的影响来重新定义节点的重要性。
首先,构造初始网络G的线形图G*,表示G中链路之间的邻接关系。
则重写式(54),得到节点在G *中的重要性:

(其中IMCG(i)是vi在G中的重要度,IMCG∗(j)是vj在G * 中的重要度。
S表示G * 中vi的对应节点集合,即初始网络G中包含vi的链接。) -
此外,通过重新定义聚集度,将节点收缩方法应用于加权网络Gw:
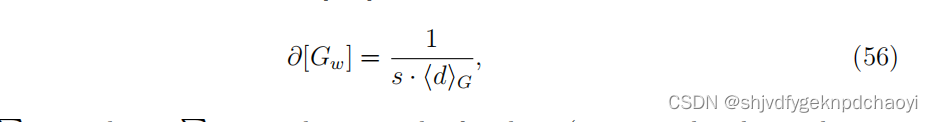 (其中s = Σi si, si = Σ j wij是节点vi的强度。注意G仍然是未加权网络中节点之间的平均距离,对应于Gw)
(其中s = Σi si, si = Σ j wij是节点vi的强度。注意G仍然是未加权网络中节点之间的平均距离,对应于Gw)
四、介绍兼顾具体动力规律和客观动力过程参数的方法。
5.Dynamics-sensitive methods 对某些给定动力过程的影响
识别关键节点的一个主要目的是找出在某些特定的动力学过程中起关键作用的节点。
因此,一个节点或一组节点对某些给定动力过程的影响通常被视为关键节点的标准。
例如,对于任意一个节点,将该节点设置为受感染的种子,然后基于(SIR)模型,将曾经受感染的节点总数作为量化该节点重要性的度量标准。
对于给定的动力学,在不同的动力学参数下,结构中心性的表现也相差甚远。所以不能构建统一模型。
例如,在SIR过程中,当传播率β非常小时,度中心性可以更好地识别有影响的扩散者,而当β接近epidemic流行阈值βc时,特征向量中心性表现更好。
研究表明,对于具有两个参数(即扩散率和恢复率)的给定SIR过程,节点影响的等级在很大程度上取决于参数。
根据上述论证,如果我们想要揭示节点在某些网络动力学中的作用,并且我们可以提前估计相关参数,那么我们应该通过考虑目标动力学的特征和参数,设计比结构中心更好的识别关键节点的方法。
因此,我们把这类方法称为动态敏感方法。
注意,在一些方法中,如LeaderRank,我们在网络上应用动态,如随机游走,但我们不调用LeaderRank作为动态敏感的方法,因为随机游走是用来对节点排序的,而它本身不是目标动态 (target dynamics)。
事实上,在关于LeaderRank的原始论文中,SIR模型的一种变体被认为是目标动态(the target dynamics)
在本节中,我们将把已知的动态敏感方法分为三类,并介绍最新的进展,并讨论一些悬而未决的问题。
1. Path counting methods 路径计数方法
原则上,任何连接节点i和j的路径都可以作为通道,将i的影响传递到j的状态,反之亦然。
因此,通过计算从这个节点到所有其他节点的路径数量来估计一个节点的影响是非常简单的,其中每个路径都被分配了与其长度相关的权重。
这一思想也体现在一些众所周知的结构中,如Katz指数和可达性(accessibility)。
本小节将介绍:路径计数思想与目标动力学的具体特征和参数相结合的方法。
一般来说,影响随路径长度的增加而衰减,衰减函数与目标动力学有关。通常采用动态特征来设计路径权值对路径长度的衰减函数。
考虑由n个节点组成的网络,其状态由一个时变实向量x = (x1,···,xn)描述。
对于任何离散耦合线性动力学( discrete coupled linear dynamics):
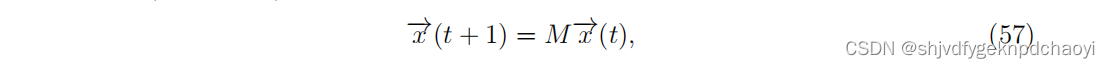
(M:n × n实矩阵,M的最大特征值µmax等于零
那么x(0)在M的左特征向量(对于矩阵A,若AX = rX存在特征向量R,则称R为右特征向量;YA=rY存在特征向量L,则称L为左特征向量。)上的投影(即:µmax)就是关于初始条件x(0)的所有信息。
记c为μ max的左特征向量,那么第i项ci量化了节点vi的初始条件对最终状态的影响程度。
ci被称为动态影响(dynamical influence:DI),用来度量vi在目标动态M中的影响。特征向量c可以通过幂迭代法来估计,该方法将M的越来越高的次幂应用到均匀向量w(0) =(1,1,···,1)
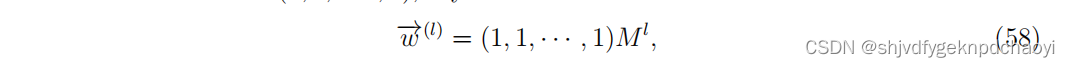
其中l是一个自然数。
如果M的最大特征值非退化(若n阶矩阵A的行列式|A|≠0,则称A为一个非退化矩阵,)且在量级上大于其他特征值,则在极限范围内可得到c:
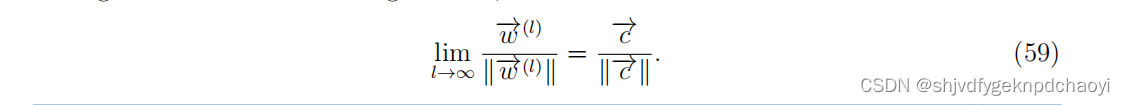
将M想像为网络的邻接矩阵,则根据式(58),wi (l)为起源于vi的长度为l的所有可能行走次数。
这个计算过程体现了DI定义背后的路径计数思想。
获得动力学影响的方法非常通用,可以应用于许多具有代表性的动力学,如SIR模型、voter模型、Ising模型、Kuramoto模型等。
-
以离散SIR模型为例,如果在每一个时间步中,受感染节点以β概率感染其每个易感邻居,然后在下一个时间步中放松到恢复状态,则动力学可表示为:
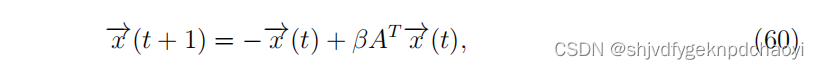
(其中xi(t)是节点vi在时间步骤t被感染的概率,A是邻接矩阵。)

(I是单位矩阵。αmax为A的最大特征值,只有当β = 1/αmax(这正是SIR模型的epidemic阈值),µmax = 0时,对于最大特征值αmax,动态影响c与A的右特征向量相同,即在这种情况下,动态影响等于特征向量中心性。 -
在易感-感染-易感(SIS)模型中,在每个时间步,一个感染节点将以概率 β感染其每个易感邻居,然后在下一个时间步中以概率(δ)返回到易感状态。
x (t)为系统状态,其第i项xi(t)为第i个节点在时间步t处处于感染状态的概率,则根据式。

由于x (t) = M^tx(0),累计感染概率向量可表示为:
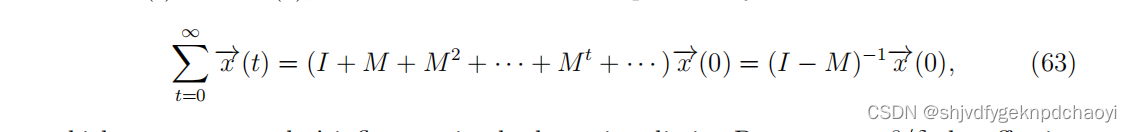
(63)表示节点在长时间内的影响。设效感染率α = β/δ,式(63)可改写为:
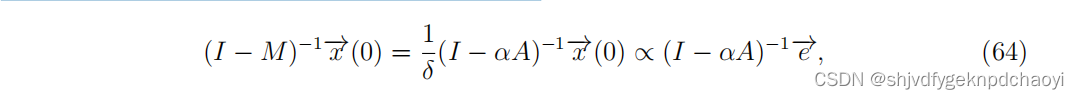
(其中e =(1,1,···,1)^T)
式(64)是一种典型的路径计数方法。
注意,这里我们假设每个节点都有相同的初始感染概率,节点的影响由其在整个传播过程中的感染频次来量化。
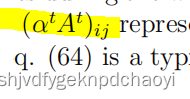
表示节点i通过具有长度t的路径去感染j的概率和。
Eq.(64)与α中心度 alpha centrality的形式完全相同:
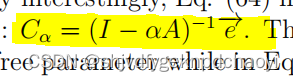
不同的是,在中心性中,参数α为自由参数,而在式(64)中,其具有明确的动力学意义α = β/δ。
SIS模型和易感感染(SI)模型中:当传播率β非常小时,度中心性可以更好地识别有影响的传播者,而当β接近流行阈值βc时,特征向量中心性表现更好。 -
Bauer和Lizier提出了一种可以直接计算SIS和SIR模型中各种长度的可能感染行走数。
它们将节点vi的影响定义为:
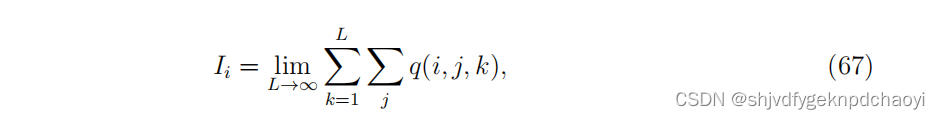
(其中j遍历所有节点,包括节点vi。q(i, j, k)是节点vj通过长度为k的路径被感染的概率,前提是感染始于节点vi,假设所有感染路径彼此独立。)
在扩散率β,返回率δ = 1的SIS模型中,采用独立路径假设,
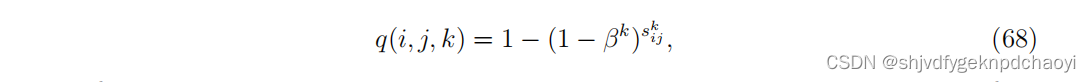 (其中skij是长度为k的从i到j的不同路径的数量,等于(Ak)ij )
(其中skij是长度为k的从i到j的不同路径的数量,等于(Ak)ij )
因此:
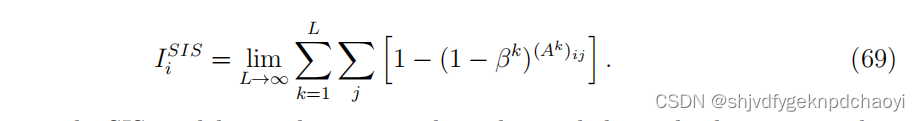
注意,在SIS模型中,一条路径可以多次经过一个节点,因此与传统的路径定义略有不同,但与walk的定义相同。
事实上,Bauer和Lizier将他们的方法称为行走计数方法。
而如果我们考虑SIR模型,对应的定义与传统意义上的路径,或者说所谓的自避式行走完全相同。
因此,当应用Bauer和Lizier的方法时SIR模型更加复杂。
Bauer和Lizier的方法直接体现了路径计数的思想,在仿真中表现得非常好,但缺点是路径无关假设太强,计算复杂度很高。
总之,他们的方法给我们留下了两个挑战:如何消除不同路径之间的相干性,以及如何有效和高效地估计路径的数量。 -
流量动态(Traffic dynamics) 是信息网络和运输网络中的另一种典型动态。
除了可能的异构包生成速率和链路带宽外,网络流量的动态特征主要由路由表决定,路由表列出了源节点vs生成的包可以传递到目标节点vt的路径。
在给定特定的路由表的情况下,Dolev等人提出了一种所谓的路由中介中心性(routing betweenness centrality:RBC) 来衡量一个节点在流量动态中的重要性。
任意节点vi的RBC定义为通过vi的数据包的期望数量 :
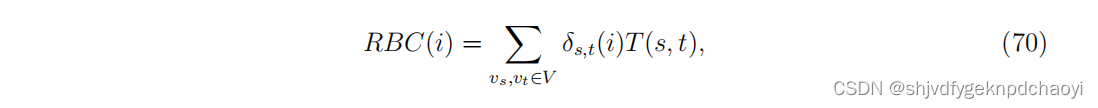
(V是网络中节点的集合,δs,t(i)是源节点vs生成的、从目标节点vt离开网络的,通过节点V的数据包的概率,t(s,t)是源节点vs发送到目标节点vt的数据包数量。)
在给定的路由表(或路由规则)下,δs,t(i)可以写成:
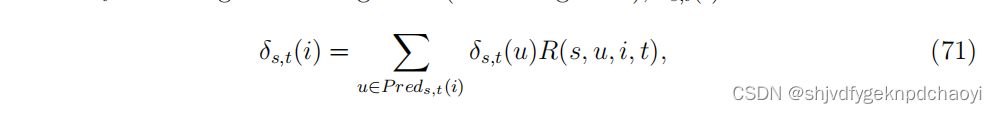
(R为路由表,R(s, u, i, t)记录vu将源地址vs和目标地址vt的信息包转发给vi的概率,Preds,t(i) = {u|R(s, u, i, t) > 0}是给定源地址vs和目标地址vt的vi的所有直接前身 (predecessors)节点的集合。)
路由中介中心性( routing betweenness centrality)是在特定的动态规则(即路由表R)下识别网络流量中重要节点的一种通用方法,它计算通过目标节点的路径数量,不同于传播动力学中计算源自目标节点的路径数量的路径计数方法。
2. Time-aware methods 时间感知方法
有时我们想知道一个节点在有限时间内对系统的影响,这就导致了所谓的时间感知方法。
- 考虑布尔网络动力学,在每个时间步中,每个节点可以处于两种状态{0,1}中的一种。
- 尽管布尔网络动力学非常简单,但它在解释和分析生物功能(如活细胞中的基因调节)和社会现象(如社交网络中的少数群体博弈)方面有着广泛的应用。
- 一般的布尔动力学:
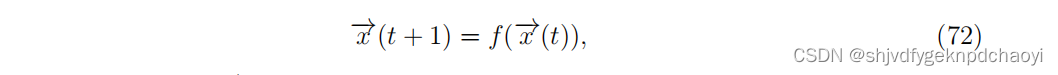
(状态向量x (t)∈{0,1}^N,f为布尔函数。)
- 任意节点vi在t时间步后的影响可以通过在vi处的扰动(即vi的状态变化)引起的系统状态的变化来量化。
- Ghanbarnejad和Klemm定义:
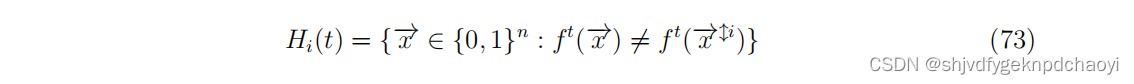
Hi(t)作为初始条件集,vi处的扰动将导致系统状态在t个时间步后发生变化,其中x^i 是状态向量,它只与x的第i个项不同。
假设所有2n个状态向量都以相同的概率出现,那么节点vi对t步的动态影响:

- 对于布尔函数f,一个待解决的问题是估计节点vi的动态影响hi(t)。
给定一个状态向量x,如果一个节点vi的变化会在下一步改变另一个节点vj的状态,则设∂(i) fj(x) = 1(fj是节点vj上的布尔函数),否则为零。
-
假设所有的都是2n状态向量以相同的概率出现,vi对v的j直接影响可以定义为:
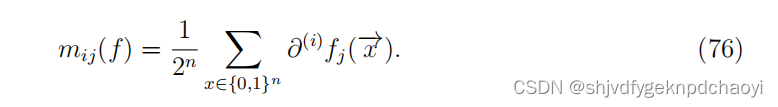
(M称为活动矩阵,它不同于邻接矩阵A,因为它包含了f的动态特征。表示pj (t)节点vj的状态在t时刻因节点vi的初始扰动而改变的概率)。 -
注意,来自不同传播路径的扰动的影响不能直接在布尔动力学中总结,因为两次翻转等于没有翻转。
-
Klemm做了一个强有力的假设,即忽略了节点影响力传播的相关性。因此,最大特征值M的特征向量可以用来量化节点在长时间内的影响。
-
Ghanbarnejad和Klemm测试了节点重要性指数与h(t)在不同t下的相关性,发现基于M的特征向量中心性优于基于A的特征向量中心性, 支持了动态敏感中心性的优势。
-
此方法并不是一个真正的时间感知方法,因为M的特征向量不包含时间信息,但是,他们的模拟结果清楚地证明了时间因素的重要性。
-
此外,对于较小的t,度中心性优于特征向量中心性,而对于非常大的t,特征向量中心性要好得多。
- Liu等人提出了一种所谓的动态敏感(DS)中心性来预测给定时间步t下的疫情规模,可直接用于量化节点的传播影响。
Liu等人使用与特征向量中心性不同的方法表明,节点在时间步t处的DS中心性可以写成一个向量

(其中A为邻接矩阵,β和δ为SIR模型的扩展速率和恢复速率。)
在时间步长为t的情况下,DS中心性优于不考虑时间因素的方法。
3. 其他方法
- 如上所述,SIR模型中节点影响的排序对于不同的参数集(β, δ)差异很大。
将任意节点vi的所谓流行epidemic中心性定义为:
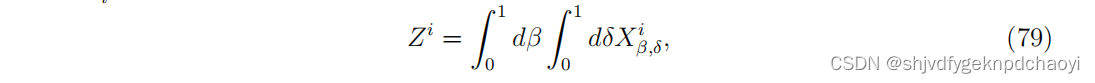
(X^i p,q:在扩散结束时处于R状态的节点的比例(传播范围))
- 有人认为,Z^i 平均应该使用一些不均匀的权重,因此:

- 目前为止,很少有研究考虑到进化博弈中关键节点的识别。
- Simko和Csermely[177]提出了一种新的动态敏感中心性,称为博弈中心性(game centrality, GC),它衡量单个背叛defecting节点将其他节点转换为自己策略的能力。
- 节点vi 的博弈中心性定义为:在过去50个模拟步骤中叛逃者defectors的平均比例,假设节点vi是叛逃者且所有其他节点都合作。
- Simko和Csermely运用博弈中心性来挖掘蛋白质-蛋白质相互作用(protein-protein interaction, PPI)网络中有影响力的节点,假设PPI网络中的功能在一定程度上可以用重复博弈来描述。
- 博弈动态扮演了在某些特定网络中寻找有影响力节点的工具的角色,就像PageRank和LeaderRank中的随机游走一样,但它不是目标动态,因此GC在这种情况下不是动态敏感的中心性。
- Simko和Csermely简要分析了GC与以前的中心性度量之间的相关性。
- Piraveenan等人提出了一种新的中心性度量,称为渗透中心性(PC),该度量考虑了单个节点的渗透状态。
-
用xi表示节点vi的渗透状态。xi = 1表示完全渗透状态,xi = 0表示非渗透状态,而部分渗透状态对应于0 < xi < 1。
-
他们没有考虑真实的渗透过程和渗透状态之间的关系,也没有讨论如何确定一个节点的渗透状态,但展示了一个例子:在一个元人口流行病模型中,对于一个乡镇网络,城镇的渗透状态将是该城镇感染人口的百分比。
-
因此,将节点vi的渗透中心性定义为:
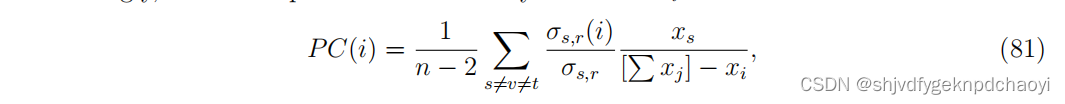
(σs,t(i):从vs到vt经过vi的最短路径数量,σs,t i:连接vs和vt的不同最短路径的总数) -
如果所有的节点在相同的渗透水平0 <µ≤1,且满足其他条件。渗透中心性退化为中介中心性。因此,渗透中心性实际上是一个加权的中介中心性,每个节点vi被分配一个权重xi,称为渗透状态。
-
原则上,这个框架允许我们将动态特征体现到权重x中。
五、将从识别单个重要节点转向识别一组重要节点,强调基于物理的方法,如消息传递理论和渗透模型。
在许多现实世界的应用程序中,我们被进一步要求找出在传播信息、维护网络连接等方面发挥关键作用的一小组重要节点。
例如,在预算有限的网络营销中,最好的策略是向一组可能购买产品的客户展示广告并提供折扣,这些客户能够触发许多其他人(包括他们的朋友、朋友的朋友等等)购买。在时间和资源有限的疫情传播中,我们需要对一部分人进行免疫接种,以最好地保护整个人群。在军事网络对抗中,需要摧毁敌人的几个关键节点,最大限度地降低敌人的通信能力。
1.Influence maximization problem(IMP)
1. Structural IMP
- 定义了网络中最重要的k个节点,即这k个节点的删除,以及所有与之相关的有向链接,将导致指定节点对之间最大流量的最大下降。
- 考虑了一个有向网络,链路权值表示两端之间的距离。那些k个节点,它们的删除将使两个指定节点之间的最短距离增加最大。
- 在传播模型中找到最小节点集,如果将其移除,则会将网络分解为许多不连接的片段。因此,一组节点S的影响的自然度量是去掉S后最大连接组件的大小。
- 对于无向网络,一个FVS是一个顶点集,它包含每个循环的至少一个顶点,因此在删除一个反馈顶点集(FVS)后,网络由一个或多个树组成。
- 反馈顶点集也被称为反循环集,所有反循环集的最小大小被命名为网络的反循环数。任意网络的反循环次数是np。
- 考虑了一个以FVS大小为目标的宽松版本:越小越好。
- 这个问题可以很容易地扩展到加权网络,其中每个节点都被赋予一个非负权,然后目标函数成为一个FVS的总权。
- 尽管FVS问题看起来与IMP的一般框架有点不同,但我们将在后面说明FVS问题非常接近IMP,最小FVS中的节点与最大影响节点高度重叠。
- 实际上,图论中的许多经典优化问题都与IMP相关,例如最小支配集(minimum dominant set, MDS)问题旨在构造一个最小规模的节点集,使网络的任何节点都在这个集合中,或者与这个集合中的至少一个节点相邻,MDS或MDS的一个子集可以被认为是IMP的近似解。
2. Functional IMP
两种简单但应用广泛的扩散模型:线性阈值模型和独立级联模型。
- 在线性阈值模型中,每个节点vi在区间[0,1]中均匀随机地选择一个阈值θi,并给每个有向链路vi→vj分配一个权重wij,满足wij≤1。一般wij ≠ wji。
- 线性阈值模型从若干初始活动节点开始,然后在每个时间步中,只有当wji≥θi时,节点vi才会成为活动节点。
- 如果节点在上一个时间步骤中是活动的,那么所有节点都将保持活动状态。
- 当节点状态不再发生进一步变化时结束。
- 独立级联模在每个时间步中,每个活动节点i都有一次机会激活vi的每个非活动邻居,比如vj,成功的概率为pij。
- 无论vi是否成功,它都不能再尝试激活它的非活动邻居。
- 同样,当不可能再激活时,该过程结束。
对于线性阈值模型和独立级联模型,影响最大化问题都是NP-hard问题。
- SIR模型非常接近独立级联模型。
如果将恢复率固定为δ = 1,同时使各环节的成功概率为常数pij = β,则两种模型相同。 - 此外,非渐进阈值模型与SIS模型非常接近。
- 因此,尽管存在一些语言和方法上的障碍,建立一种连接计算机科学家和统计物理学家的方法,从而找到更好的解决影响最大值化问题的方法是可以期待的。对同步、进化博弈和运输等其他动力学的影响最大化问题的研究还很少,这也是一个值得进一步探索的有趣问题。( studies on influence maximization problem on other dynamics, such as synchronization, evolutionary game and transportation, are rarely reported, which is also an interesting issue for further explorations)
3.Heuristic and greedy algorithms 启发式和贪婪算法
由于典型的信息最大化问题是NP-hard,大多数已知的工作试图寻找近似解而不是精确解。
- 启发式算法是所有近似算法中最常见的,例如,根据节点度或另一种中心性度量对所有节点进行排序,并直接选取k个排名靠前的节点是k的一种算法。
- 另一类被广泛研究的算法是贪婪算法,它将节点一个一个地添加到目标集合中,确保每一次添加都会给前一个集合带来最大的影响增加。
1. Heuristic algorithms
最直接的方法是根据一定的中心性度量(如度和betweeness介间性)直接选取top-k节点。
然而,如上所述,这种方法可能是低效的,因为度最大或介间性最大的节点可能是高度聚类的。
通过自适应重新计算,可以取得轻微的改进,即先选择中心性最大的节点,然后在每一步节点去除后重新计算节点的中心性。
- 类似于重新计算的思想,Chen等人提出了一种所谓的度折现算法,其精度与贪心算法[200]几乎相同,但运行速度比最快的贪心算法快一百万分之一以上。
- 考虑每个环节激活率恒定的独立级联模型,pij = p。
- 设节点vi和vj相邻,如果vj已经被选为种子,那么在考虑是否根据vi的度数选择vi为新种子时,我们应该将vi的度数打折,因为链接(i, j)对传播过程没有任何贡献。
- 设si为vi已经被选择为种子的邻居数,则应将vi的度折现为k’i = ki−si
- 许多真实的网络表现出社区内的联系是密集的,而跨社区的联系是稀疏的。意味着社区内的节点比跨社区的节点更有可能相互影响。
因此,在选择一组影响者时,选择不同社区的节点比选择整个网络更有效。
基于这一想法提出了一种基于社区的方法来寻找位于不同社区的前k名有影响力的传播者。
- 首先,利用社区检测算法[7]将网络划分为多个社区;
- 然后,所有社区根据其规模按递减顺序排列。
- 根据一定的中心性指标(如选择度最高的节点)从最大的社区中选择第一个散布节点。
- 类似地,在第二大社团中具有最大中心性指数且与前一个社团没有边关联的节点(对于第二个所选的散布节点,前一个共同体只有一个)被选为第二个散布节点。
- 如果访问了所有的社区,并且选择的传播者数量不够,我们重新启动上述过程,并按照相同的规则选择剩余的传播者,直到找到k个传播者。
用这种方法选出的有影响力的散布者更有可能分散分布在网络中。
- 根据信息传递概率矩阵将网络划分为k个社区,然后选择k个中位数作为k个散布节点。
- 为了得到信息传递概率矩阵,将每条边(i, j)分别指定为“以βij的概率开”或“以1 - βij的概率闭”,其中βij是传播概率和边的权重wij。
- 对于非加权网络,这一过程类似于网络上的键渗透。
- 对于两个节点vi和vj,如果它们之间至少有一条由“开边”组成的路径,则ω(i, j) = 1,否则为0。
- 定义了信息传递概率矩阵的元素mij,为不同试验ω(i, j)的平均值。
- 该方法使用最常见的k-medoid聚类算法Partitioning Around Medoids实现,时间复杂度为O(k(nk) 2)量级,非常耗时,因此难以应用于大规模网络:
- 基于与基于社区的方法类似的考虑,Zhao等人将网络划分为几个独立的集合,其中一个独立集合中的任何两个节点彼此不相邻。
- 这个任务在图论中被称为图着色,每个节点被分配一种颜色,相邻的两个节点不能共享相同的颜色。
- 为了给网络上色,采用了著名的wells - powell算法,该算法需要的颜色数量非常少,时间复杂度O(N2)相对较低。
- 在给定一定中心性指标的情况下,选取独立集合中规模最大的top-k节点(即颜色最流行的节点),形成目标集。
- 通过在Barab´asi-Albert网络和两个受接触过程(SIR模型的变体)影响的真实网络上进行测试,Zhao等人表明,他们的方法可以提高许多已知中心的性能,包括度、中间性、亲和度、特征向量中心性等。程度和中间性的改善尤其巨大。
- 基于图的启发式最优划分,Chen等人提出了一种所谓的等图划分(EGP)策略,在划分网络时,该策略的性能明显优于简单选择最高的度量值或最高的中间性节点。
- EGP策略基于嵌套分解(ND)算法,该算法可以将一个网络分离为两个大小相等的集群,删除的节点数量最少。
- Chen等人通过递归地应用ND算法将网络划分为任意数量的大小相等的集群。
为了免疫一个有n个节点的网络,使只有F的一小部分可以被感染(即巨型组件的大小不超过Fn), Chen等人将网络分成 n’ ≈ 1/F 等大小的集群。 - 因此,在给定目标F的情况下,EGP将产生所需节点的最小数量,这些节点可以被认为是IMP所需的有影响力的节点集。EPG策略接近全局优化,因此比局部算法更耗时。
- 注意,EPG策略不能直接应用于求解k-IMP,因为EPG的影响节点结果集的大小取决于F。
2. Greedy algorithms
设计贪心算法的一个自然想法是,确保每向目标集(即最初感染或激活的种子集)添加一个节点,都会使增量影响最大化。f(S)表示一组节点S的影响,可以通过,例如,SIR模型中曾经受感染的节点的数量来量化。
Kempe, Kleinberg和Tardos最早提出了函数IMP的贪婪算法,他们的算法从一个空目标集S =∅开始,在每个时间步中扫描所有节点,找到f(S∪{v})最大化的一个v∈v \S,然后更新为S←S∪{v}。
经过k个时间步,得到包含k个影响节点的目标集S。
-
为了了解近似保证,我们首先引入子模的概念。
将有限集映射为非负实数的函数f是子模函数
如果向集合S中添加一个元素的边际增益不小于该边际增益
将相同的元素加到s的超集,形式上,子模函数满足:
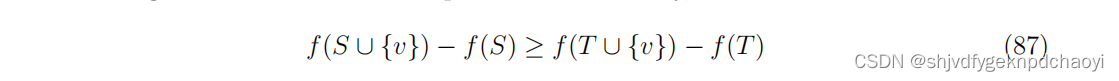
对所有元素v和所有集合S⊆t。如果f是单调的,即f(S∪{v})≥f(S)。对于所有元素v和集合S,则证明了上述贪婪算法(即最简单的爬坡算法)近似于最优S∗
在因子1−1/e≈0.63内,即:

Kempe等证明了在独立级联模型和线性阈值模型的情况下,在期望激活节点数f(·)上的目标函数都是子模的,因此贪婪爬坡算法提供了(1−1/e)-逼近。
如参考文献所示,贪婪爬坡算法比简单地选择最高度degree或最小接近度closeness的top-k节点的性能要好得多。 -
在独立级联模型中,与连接(i→j)相关的激活概率pij与动力学过程的历史无关。
然而,社交网络中的信息传播表现出记忆效应。
因此,Kempe进一步将独立级联模型扩展为所谓的递减级联模型,其中pij依赖于历史。
S是vj的邻居节点且已经尝试激活vj的节点集合,则vi成功激活vj的概率为pij (S)。 -
递减级联模型包含两个自然约束
1) 顺序无关:如果集合T中的所有节点都尝试激活节点vj,那么它们尝试的顺序不影响vj最终被激活的概率;
2)非递增:函数pij (S)满足不等式pij (S)≥pij (T)时,S⊆T. Kempe等人证明了降低级联模型的目标函数f(·)也是子模的,因此贪婪爬坡算法提供了(1−1/e)-逼近。
原始贪婪算法的一个明显而严重的缺点是它非常耗费时间。
-
对于n节点m链路网络上的k-IMP,如果为了从一组种子S中准确估计激活节点的期望数量f(S),需要对给定的动态过程进行R次直接模拟,则时间复杂度为O(kRNM)。
-
实际上,对于成千上万个节点,k≤100的小型网络,完成该算法需要几天的时间。
-
因此,原有的贪心算法不能直接应用于现代信息社会的大规模网络。
- Leskovec等人注意到子模块性,当向种子集S中添加节点vi时,如果S更小,则边际增益f(S∪{vi})−f(S)更大(或至少相等)。
-
因此,Leskovec等利用在寻找边际增益最大节点的每一个时间步中,大量节点不需要重新评估,因为它们在上一轮的边际增益已经小于当前时间步中评估的其他一些节点,提出了所谓的成本效益惰性向前(CELF)算法。
-
正如中所报道的,对于某些特定的网络实例,CELF算法比原始的贪婪算法快700倍。
- 提高原有贪心算法效率的另一个方向是加快获取预期激活节点数f(S)的过程。
事实上,直接模拟扩散动力学,如独立级联模型和SIR模型是非常低效的。可以通过键渗透快速估计f(S)。
-
利用这种等价性来加速原有的贪婪算法。
-
考虑到独立级联模型,对于每一次R运行,Chen等人[207]以1−pij的概率从G中删除每个链接(vi→vj),生成网络G0(即得到渗透网络)。
-
设RG0 (S)是G0中S可达节点的集合,则对G0进行线性扫描(通过深度优先搜索或广度优先搜索,时间复杂度O(M)),可以得到所有节点vi∈V的RG0 (S)和RG0 ({vi})。
-
那么对于每个节点vi∈V \S,如果vi /∈RG0 (S),将vi加入S的边际增益要么是|RG0 ({vi})|,要么是vi∈RG0 (S)为0。该算法的时间复杂度为O(kRM),原则上比原始贪婪算法快N倍。也比CELF算法快。
3.Message passing theory 消息传递理论
消息传递理论首次被开发用于处理高维无序系统,该理论量化了可以用离散变量上的静态约束满足模型表示的动态中解决的概率。
本节将介绍两个示例。
- 前者是针对典型的结构IMP(Influence maximization problem)- FVS问题提出的,它也可以扩展到另一个结构IMP——最优渗流问题。
FVS(反馈顶点集问题): 从图G中删除该集合中的所有点后,图中 不含圈,即图G中的每个圈至少有一个点在FVS中。
- 后者是针对典型的功能性IMP提出的,即在线性阈值模型中寻找最具影响力的播种者作为初始种子,使最终活动节点的期望数量最大化,也可用于寻找最能保护整个网络的小范围免疫节点集。
1.示例一
一种高效的消息传递算法,其核心思想是将全局周期约束转化为一组局部约束。
-
让我们考虑一个无向简单网络G,在每个顶点vi上定义一个状态变量Ai,它可以取值Ai = 0, Ai = i,或Ai = j∈Ti,其中Ti是vi的邻居集合。
-
如果Ai = 0,我们说顶点vi未被占用,如果Ai = i,我们说顶点vi已被占用,并且它是一个没有任何父顶点的根顶点,如果Ai = j∈Ti,我们说顶点vi已被占用,vj是它的父顶点。
-
将任意边(i, j)的边因子Cij (Ai, Aj)定义为:
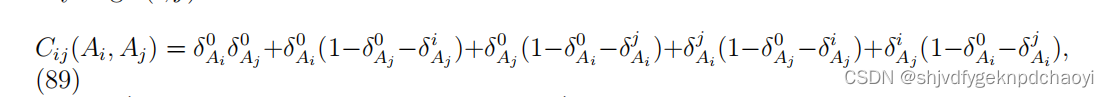
其中δi j是Kronecker符号,当i = j时δi^ j = 1,否则为0。
边缘因子Cij (Ai, Aj)的值要么为0,要么为1,只有在以下五种情况下,Cij (Ai, Aj) = 1:
(1)顶点vi和顶点vj都未被占用;
(2)顶点vi未被占用,而顶点vj已被占用,且vi不是vj的父结点;
(3)顶点vj未被占用,顶点vi被占用,并且vj不是vi的父结点;
(4)顶点vi和顶点vj都被占用,vj是vi的父结点,而vi不是vj的父结点;
(5)顶点vi和顶点vj都被占用,vi是vj的父结点,而vj不是vi的父结点。 -
对于微观构型A = {A1, A2,···,AN},我们将每条边(i, j)视为一个局部约束,当Cij (Ai, Aj) = 1时,满足某条边(i, j),否则不满足。
如果一个微观构型A满足网络G的所有边,那么它就作为这个网络的解决方案。
- 让我们把c树定义为一个连通图,它只有一个n≥3个顶点 & n条边的环。
可以很容易地证明:网络G的任何解A的被占用顶点可以导出一个具有一个或多个连通组件的子图,其中每个组件要么是树,要么是c树。
G的解与反馈顶点集合密切相关,因为我们可以随机地从每个c树的循环中移除一个顶点将子图诱导成森林,使剩余的节点形成反馈顶点集。
因此,具有更多被占用节点的解决方案通常对应较小的FVS(这并不完全正确,因为解可能包含大量的c树,但是我们不认为这种不正常的情况)。
直到现在,正如开头所提到的在本节中,我们将原始的FVS问题转化为静态约束满足问题离散变量模型。
- 据此,Zhou定义了的配分函数系统如下:
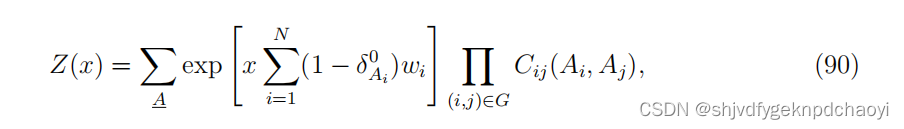
(其中wi≥0是每个顶点vi的固定权重,x是一个正的重新加权参数,项Π (i,j)∈g Cij (Ai, Aj)保证只有解对配分函数Z(x)有贡献。)
qi^Ai表示顶点vi获得状态Ai的边际概率,该状态很大程度上受vi的邻居状态的影响,同时vi的状态也会影响其邻居的状态。
在计算qi^Ai时,为了避免过度计数,我们可以先从网络中去除顶点vi,然后在剩余的网络中考虑集合Ti的所有可能的状态组合,称为空腔网络。
注意,在空腔网络中,Ti中的顶点可能仍然是相关的(只有当G是树时,它们才没有被校正),而我们忽略了所有可能的相关性,并假设概率的独立性,这在统计物理学界通常被称为贝特-佩尔斯近似或相关衰减假设,如果网络局部像树一样,则效果很好(当网络非常稀疏时,这种情况几乎是如此。
而真正的网络通常是非常稀疏的)。
根据贝斯-佩尔斯近似,联合概率近似因式分解为:
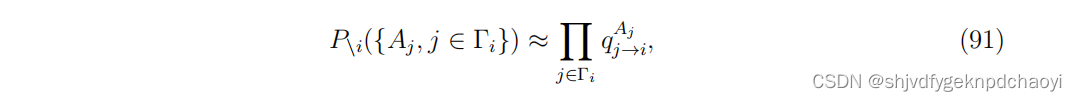
其中q (j→i) ^Aj 表示空腔网络中状态Aj的边际概率,其中不考虑顶点vi的影响。
如果所有顶点vj∈Ti在空腔网络中要么是空的(Aj = 0),要么是根(Aj = j),那么vi加入网络时可以是根(Ai = i)。
这是因为在添加了vi之后,相邻顶点vj可以将其状态变为Aj = i。
同样,如果一个顶点l∈Ti在空腔网络中被占用,而Ti中的其他顶点在空腔网络中都是空的或者是根的,那么vi在加入到网络中时可以取状态Ai = l。
这些考虑,加上贝斯-佩尔斯近似(Eq.(91)),得到qi ^Ai的以下表达式:
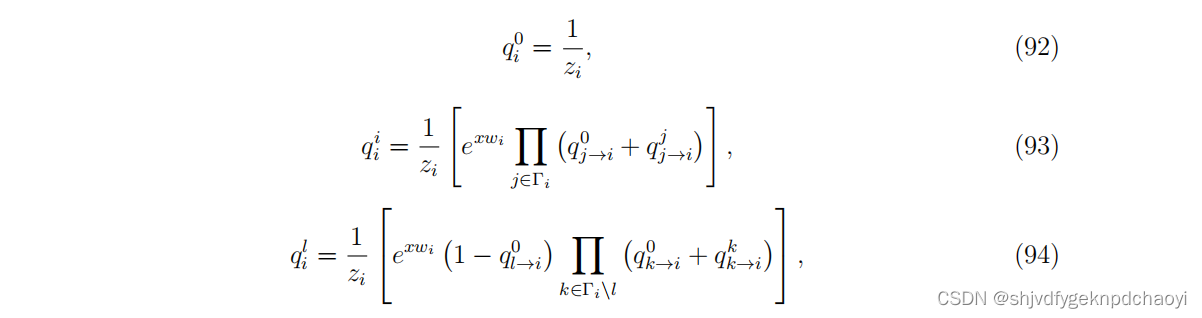
2.示例二
Altarelli等人考虑了渐进扩散动力学的IMP,即线性阈值模型,它比FVS问题更复杂。
线性阈值模型 : 从若干初始活动节点开始,然后在每个时间步中,只有当wji≥θi时,节点vi才会成为活动节点。
-
记xi^t为时间步t时节点vi的状态,线性阈值模型以少量活动种子xi ^ 0 = 1开始,更新规则读取:
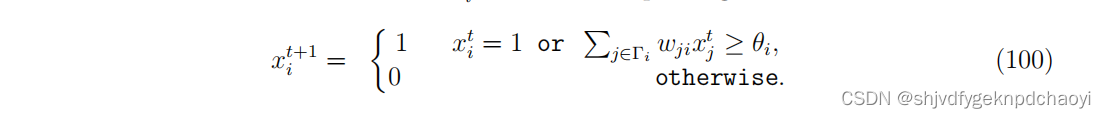
用ti表示节点vi的激活时间(初始种子为ti = 0,最终状态不活跃的节点为ti =∞),则动态过程的演化可完全用构形t = {ti}, vi∈V表示。 -
在线性阈值模型中,相邻节点的激活次数之间的约束为:
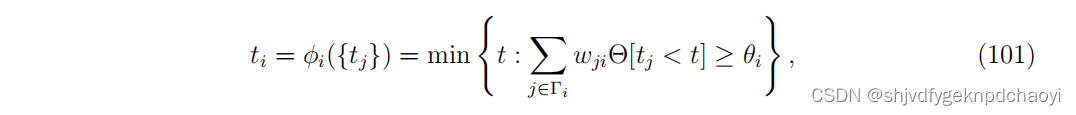
(Θ[·]= 1,如果[·]中的条件为真,否则为0。) -
因此,线性阈值模型的解 t 满足约束:
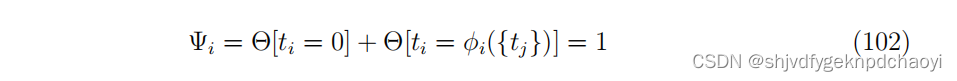
-
对于每个节点vi,可以把配分函数写成:
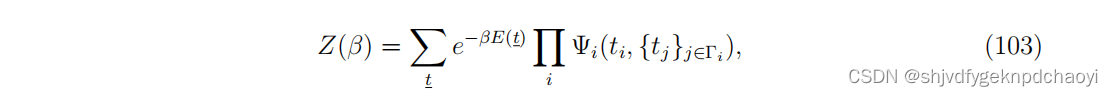
(其中E(t) = Σi Ei(ti), Ei(ti)是在时刻 ti 时激活节点 vi 所产生的成本(目标函数)(如果为正)或收益(如果为负)。 -
Altarelli等人[255]将能量函数设为:
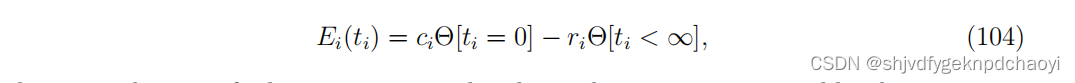
(其中ci是选择vi作为种子的成本,ri是激活vi产生的收益。)
与FVS问题不同的是,如果只考虑单个变量 ti 的约束条件,因子网络将由多个短循环组成,相关衰减假设就不成立。
4.Percolation methods 渗流方法
网络渗流可分为bond Percolation 渗流和 site Percolation 渗流。
- 给定无向网络G(V, E),在bond渗透中,每条边以p的概率保留(即被占用),以1-p的概率去除。
当p = 0时,将删除所有链接。随着p的增加,更多的链接被保留并形成一些小的簇。 - 只有当p大于临界阈值pc时,才会出现O(|V |)大小的巨大连接组件。
- 这一过程与站点渗透类似,不同之处在于保留概率p被分配为节点而不是边。
易感-感染-恢复(SIR)模型中,节点vi的影响可以通过以vi为初始种子的最终感染节点的数量来衡量。
- 研究SIR模型的静态性质与bond渗流之间的关系,表明传输率为p的SIR模型等价于网络上bond占用概率为p的键渗流模型。
考虑到这种自然关系,提出了一种基于键渗透的方法,以确定给定数量的有影响力的扩散者的最佳组合。
- 为了找到W个有影响的节点,在给定概率p的条件下,每条边将以p的概率被移除,移除链接后将出现m个孤立的集群。
1)用Si(i = 1,2,····,m)表示簇 i 的大小,L(≥W)是一个可调参数,如果L≤m,则选择最大的前L个簇,并给每个簇中最大的度节点分配1分。(如果度最大的节点很多,随机选择一个。)
2)当m < L ≤ 2m时,首先选取每个集群中度数最大的节点,其余L−m节点分别从top - (L−m)个集群中度数第二大的节点中选取。
3)如果L > 2m,则按照相同的规则选择每个集群中第二大度数节点。
4)经过多次不同的链接删除试验后,所有的节点根据它们的分数降序排列。建议评分最高的W个节点作为初始散布子集。
该方法可并行计算,复杂度为O(t|V |)。
与传统方法 “度、介度、紧密度、k壳等” 非协调spreaders传播节点相比,渗透法识别的spreaders在网络内分布均匀,大大提高了传播覆盖率,减少了冗余。
- 与寻找给定数量的有影响力的扩散者相比,寻找可以优化全局影响函数的最小节点集更为复杂,被证明是NP-hard问题。
- 最近,Morone等人指出,寻找可以优化全局影响函数的最小节点集,可以精确地映射到网络的最优渗透。
- 思想基于网络站点的渗透,主要任务是找到对网络的全局连通性至关重要的最小节点集。
1)考虑一个有n个节点和m条边的网络,让向量n = (n1,, nn)表示网络中哪个节点被删除(ni = 0,影响者)或保留(ni = 1), q = 1−1/nΣ i ni 。
2)序参数vi→j,表示:在删除节点vj的网络中,节点vi在大组件中的概率。(i→j表示从vi到vj的链接。)
3)给定q(≥qc)的最优影响问题可以改写为:寻找向量n使得最大特征值λ最小。在线性算子M(2m × 2m有向边)上。
4)通过极值优化(EO)方法最小化多体系统的能量可以找到解决方案。
由于EO无法在大型网络中找到最优配置,因此提出了一种名为“集体影响”(CI)的可扩展算法。
- 由于信息在网络上的传播是一个全球性的过程,一般认为要使传播覆盖率最大化,就需要整个结构的信息,如上述方法。
- 受著名的社会传染现象——“三度影响(即任何个人的社会影响超过三度就停止了)”的启发,胡等通过将传播动力学(SIR家族)映射到复杂网络上的纽带渗透,发现了SIR家族传播的一个关键规律——传播发生在两个状态之一,局部阶段和全球阶段。
- 前者对应的是活动节点数量非常有限的受限传播,而后者对应的是广泛传播阶段,其规模与整个网络的顺序一致,其分数与初始种子和实现无关。
- 利用特征局部长度标度将整体阶段和局部阶段区分开来,可用于预测和量化扩散早期几个步骤的结果。
这揭示了一个结果,即一个节点或一组节点的全局影响力可以通过纯局部网络信息来精确测量。 - 他们对这种类似于渗透跃迁中相关长度的局部长度尺度的存在进行了理论解释,得出节点的影响等于巨分量大小与该节点属于巨分量概率的乘积。
- 对于一组规模远小于网络规模的W个节点,其总体扩散影响等于巨组件规模与至少m个节点集群被W个spreaders激活的概率的乘积。
- 这里m是一个阈值参数,由临界现象的相关长度决定。
- 为了找到最佳的W-spreaders,他们提出了一种基于渗透的贪婪算法,该算法给出了一个计算时间与网络规模无关的近似优化解。
六、特定类型的网络:在加权网络上 On weighted networks
1. Weighted centralities 加权中心
1.节点强度
考虑一个无向网络,对于任意节点vi,其强度定义为与vi相关的链接的权重之和,即:

节点强度集成了关于其连通性和相关链接重要性的信息。当权重独立于拓扑时,我们有s ≈ k,其中是平均权重。而在实际加权净值中,强度与度呈非线性相关关系,如s 相关于k^θ和θ ≠ 1。对于有向网络,我们还可以定义in-strength和out -strength,它为:
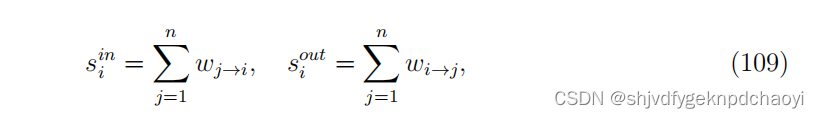
其中wi→j是节点vi到节点vj的有向链路的权值。通过归一化节点强度,得到加权度中心性为:
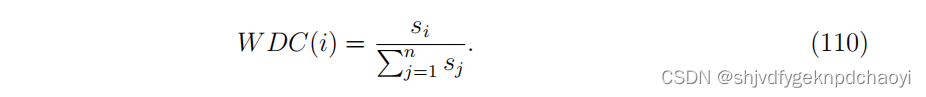
2.Weighted coreness 加权核数
经典的k壳分解可以通过在修剪(即节点去除)过程中重新放置具有加权度的节点度来扩展到加权网络。
除了节点强度,Garas等人通过考虑度和强度的总和来定义节点的加权程度,可写成:
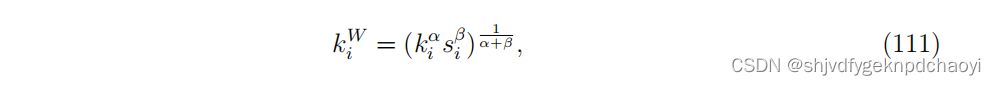
(k ^ i是v ^ i的度, α和β为可调参数。
当α = 1, β = 0时,ki ^W = ki对应经典的k壳层分解。
当α = 0, β = 1时,ki ^W = si表示s壳/s核分解[280]。
当α = β = 1时,ki ^W =√kisi,表示权值和度相等)
加权网络中的k核分解过程与非加权网络中的k核分解过程非常相似。唯一的区别是加权度通常是非整数。
3.Weighted H-index 加权h指数
h指数在加权网络上的扩展比在有向网络上的扩展要复杂得多。
节点vi的加权H指数是通过H函数作用于vi的邻居的加权度(这里以节点强度为例)与相应的链路权值相关联的级数.
4.Weighted closeness centrality 加权紧密中心性
将紧密中心性扩展到加权网络的关键点是对最短路径的重新定义。 加权网络中链路的距离与其权重有关。
例如,通过高带宽的以太网连接下载文件比通过低带宽的以太网连接下载文件要快。
从效率的角度来看,高带宽连接可以缩短站点之间的距离。
由于大多数加权网络中的链接权重是链接强度的操作化,而不是它们的成本,Newman都提出采用权重的倒数来扩展紧密中心性和中介中心性。
两个节点vi和vj之间的距离定义为:
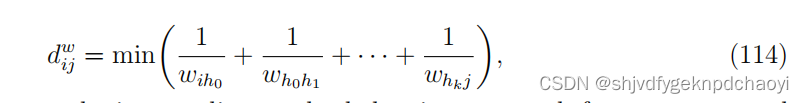
其中vh0、vh1、···、vhk是属于从vi到vj的路径的中间节点,通过Dijkstra算法可以得到使”1 / 权重“之和最小的最短路径。
则加权的密切度中心性可表示为:
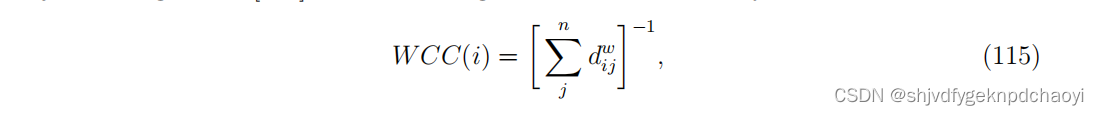
显然,这个定义忽略了中间节点数量的影响,即vh0, vh1,···,vhk。
Opsahl认为这个数字是一个重要的特征,并重新定义了最短路径的长度,写为:
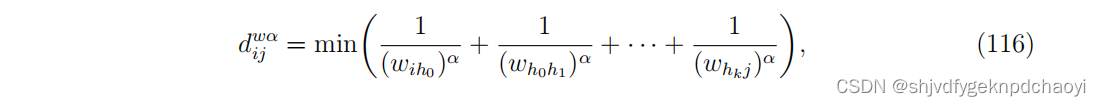
(α是一个正的可调参数。
当α = 0时,其结果与无权网络中的距离相同;
当α = 1时,结果与式(114)相同。
当0 < α < 1时,较短的路径(中间节点较少)优先被分配为较短的距离。
相反,当α > 1时,附加的中间节点的影响小于联系的权重,因此较长的路径更受青睐。)
因此,加权接近度定义为:
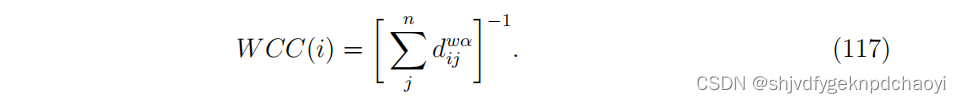
5. Weighted betweenness centrality 加权中介中心性
作为一种基于路径的中心性,将中介中心性扩展到加权网络还需要新的最短路径定义。
除了加权紧密度中心度 weighted closeness centrality外,加权中介性中心性Weighted betweenness centrality可通过式(114)定义为:
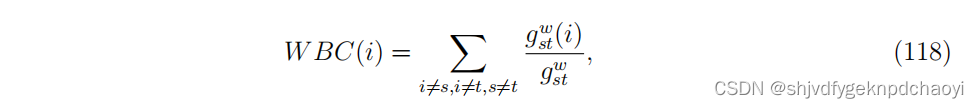
(其中gst^w是vs到vt的最短路径的个数,gst ^W (i)是vs到vt经过节点vi的最短路径的个数。)
考虑中介节点的影响,定义最短路径为式(116),对应的加权中介中心性:
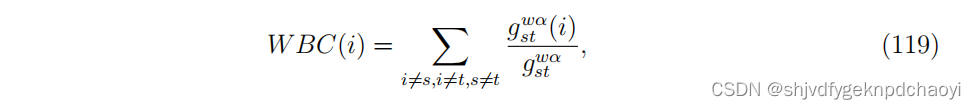
(其中α是一个正的可调参数。)
4. Weighted PageRank and LeaderRank
-
PageRank向加权网络的扩展简单明了。在每一步中,一个节点的PR值将根据链路权重分配给它的出路outgoing节点。也就是说,将随机游走过程替换为加权随机游走。
数学上,我们有: (s除以j等于vj的强度。)
(s除以j等于vj的强度。) -
类似的扩展也可以应用于加权的LeaderRank算法。
首先,在加权网络中增加一个接地节点,同时增加接地节点与n个网络节点之间的双向链路;
用W LR(t)^i表示节点vi在时间t时的加权LeaderRank分数。最初,每个网络节点分配一个单位分数,地面节点分配零分数。
那么加权的LeaderRank分数为:
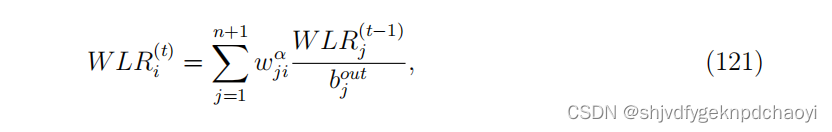
5.D-S evidence theory
如果一个节点有更多的邻居或更高的强度,它就被认为更重要。
- Dempster-Shaper (D-S)证据理论很好地综合了这两个因素来量化节点的重要性,该理论是不确定性推理的一般框架。需要更弱的条件(不需要满足概率的可加性)。
- 它同时具有“不确定”和“未知”两种状态。
- 在识别重要节点的情况下,D-S证据理论将分别估计节点vi重要和不重要的概率,也允许对这个问题的节点度是未知的。
- 由于节点重要性的度量只需要完整D-S证据理论中的一些基本理论,我们直接给出了计算过程。
节点的重要性被认为与节点的度和强度高度相关。
这两个因素的影响可以简单地用高、低两个评价指标来表示,形成θ =(高、低)的识别框架。
很容易得到:
- kM = max{k1, k2,…}, km = min{k1, k2,…}, sM = max{s1, s2,…}和 sm = min{s1, s2,…}。
- 然后分别建立节点的度和强度的基本概率分配。
- 其中,mdi(h)表示考虑程度影响时vi重要的概率,mdi(l)表示vi不重要的概率。
考虑节点的强度,msi(h)表示vi重要的概率,msi(l)表示vi不重要的概率。
具体情况如下:
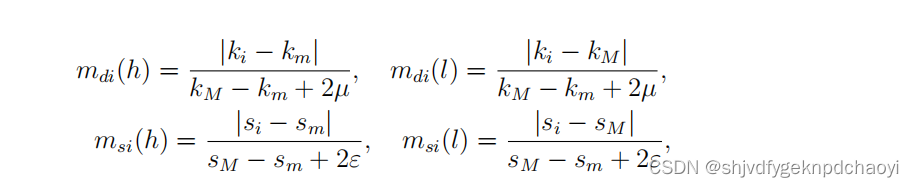
(其中0 <µ,ε < 1表示节点顺序的一种不确定性。他们的值对节点顺序没有影响。)
vi的度 & 强度的关系(BPA):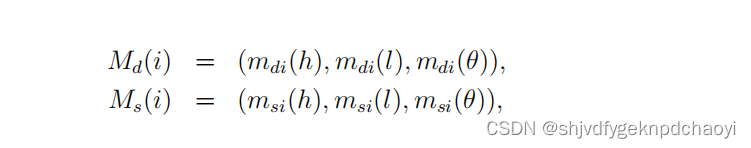
- 在mdi(θ)= 1−(mdi (h) + mdi(l),和msi(θ)= 1−(msi (h) + msi (l))。
- mdi(θ)和msi(θ)的值表明D-S证据理论不知道vi是否重要。
通过引入登普斯特组合规则,vi的影响值可表示为:

一般来说,mi(θ)的值平均分布于mi(θ)和mi(θ)。
因此:
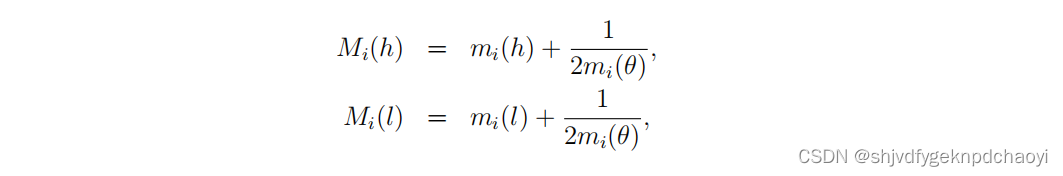
(Mi(h)和Mi(l)分别是vi重要和不重要的概率。)
- 显然,Mi(h)越高和/或Mi(l)越低,vi就越重要。
因此,基于证据理论的证据中心性可以定义为:

- 存在节点度服从均匀分布的隐式假设,这限制了算法的有效性。
- 此外,EVC中心性被认为忽略了网络的全局结构信息。
为了解决这些问题,将半局部中心性的扩展与考虑度分布影响的修正证据中心性相结合,提出了一种改进的度量方法——证据半局部中心性。
此外,还引入节点邻居之间的拓扑连接,即局部结构信息,以增强证据中心性的有效性。
七、特定类型的网络:On bipartite networks 二部网络
与单部网络不同,二部网络是由两组节点组成的。只允许不同组中的节点进行连接。
给定一个网络G(V, E),其中V和E分别是节点和边的集合。
- 如果V可划分为两个子集X和Y,且满足X ∩ Y =∅,且同一子集中两个节点之间没有边相连,则称G(V, E)为二部网络,用B(X, Y, E)表示。
许多常见的网络是二部网络,尽管它们可能不能用二部图来表示,其中两组节点被清楚地区分开来,如树和四方格。
例如,异性关系可以用双侧网络来描述,男性是一个群体,女性是另一个群体。
- 代谢网络是化学物质和化学反应作为两个互不相连的子集的二部网络。
- 协作网络是参与者和事件作为两个互不关联的子集的二部分网络,如科学家或电影演员之间的协作。
- 互联网电话网络是一种双部网络,其边缘连接用户ID和电话号码。
- 另一个代表性的例子是在线电子商务网络,它由用户-对象二部网络(bipartite network)提出。
二部网络有许多特殊的特点:
- 它们没有奇数长度的回路
- 可采用二色;
- 具有对称的网络谱。
基于这些特征,我们可以通过广度优先搜索或其他方法来判断无向简单网络是否是具有线性时间复杂度的二部网络。
1. Reputation systems
在许多在线社区中,用户可以自由地对相关项目(如电影、音乐、书籍、新闻或科学论文)发表评论。
因此,建立一个信誉系统是非常必要的,对用户的信誉和商品的质量进行可信的评价,以减少当事人之间的信息不对称所造成的损害。
这是二部网络中关键节点(即高信誉用户和高质量物品)识别的具体问题。
通常,假定一个在线社区由n个用户和m个项目组成,可以很自然地用二分网络G(U, I, W)表示。
其中U和I是用户集(用拉丁字母标记,I = 1,2,···,n)和项集(用希腊字母,α = 1, 2,···,m)。如果用户i进行了交互,则用户i和项目α之间存在加权链接。
W表示相互作用的集合用户和项目。连接wiα的权重由相互作用的类型决定,对应的(用户-项目)对反映了交互的强度。W可以是有向的也可以是无向的。
- 例如,在在线评分系统中,如果用户i对项目α用riα评分,则wiα = riα,否则wiα = 0。
- 而有时候,商品的卖家可以同时对用户进行评分,在这种情况下,我们可以使用有向网络,其中wiα ≠ wαi。
- 对于未加权的用户-商品网络G(U, I, E),设用户I购买,读取或查看项目α时:eiα = wiα = 1,否则eiα = wiα = 0。
- 也可以通过设置eiα = 1( if wiα > w0)化简加权,将网络转换为其无权重版本。
w0∈[0,wmax)为选择阈值。w0越大,网络越稀疏。
2. Statistical methods 统计方法
- 名誉系统中,量化商品质量Q最直接的方法是使用平均评分(缩写为AR),Qα = 1/kα Σi riα,其中来自不同用户的评分贡献相等。
然而,声望用户的评分应该比不忠实用户的评分更可靠。
因此,计算一个项目的质量可以被定义为:

(Ri为用户i的归一化声誉评分,可为外生参数,或者由他之前对物品的评分决定)
- 一种基于组的排名(GR)方法来量化用户的声誉。
首先根据用户的评分模式对用户进行分组,然后计算分组的规模。
基本假设是,总是属于大群体的用户更有可能拥有较高的声誉。
GR方法有五个步骤:
(1)列出系统中存在的分数,即{ω1, ω2,···,ωns},其中ns为不同分数的个数;
(2)构造得分项矩阵Λ,其中Λsα为对项目α打分ωs的用户数量;
(3)构建评分-奖励矩阵Λ∗, Λ∗Sα = Λsα/kα;
(4)将原始评价矩阵映射为奖励矩阵A,其中A’ia = Λ*sα,约束条件为riα = ωs。
注意,如果用户i没有对α项打分,A’ia的值为空,在接下来的计算中将忽略它;
(v)通过A’i的均值与其标准差之比计算用户i的信誉Ri,即:
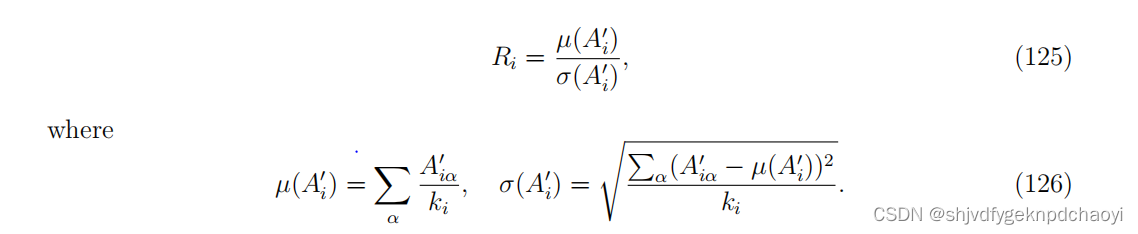
3.Iterative methods
可以通过迭代的方式计算用户信誉和项目质量。
- 其中,商品在t时刻的质量Q^(t) ,根据用户在t−1时刻的声誉R^(t−1) 表示。
- 而用户在t时刻的声誉则是根据商品在t−1时刻的质量来计算。
- 迭代从设置Q^(0) 或 R^(0)的初始值开始,当Q和R都收敛时停止。
根据这一思想提出了许多方法。
-
Laureti等人提出了一种迭代细化(IR)方法,该方法认为用户的信誉评分 & 用户评分记录与物品质量之间的均方误差成反比,即:
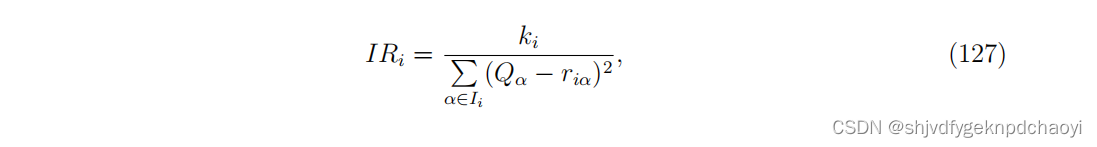
( 其中Ii为用户i选择的项目集合。)
将这个方程与Eq.(124)结合起来,我们可以开始一个迭代过程,IRi(0) = 1/| i |来计算Q和IR。注意,在每次迭代中IRi都应该是标准化的。 -
Zhou等人提出了一种基于相关性的迭代方法(简称CR),该方法假设用户的口碑可以通过用户的满意度与相应商品质量之间的关系来反映。
具体来说,采用皮尔森相关系数:
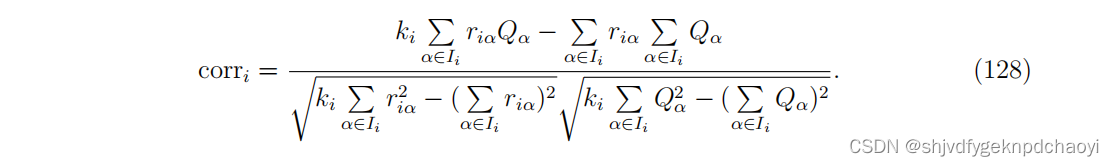
(如果corri≥0,则用户信誉CRi = corri,否则CRi = 0。)
在这里,我们也可以利用式(124),通过将Ri替换为CRi,并取初值CRi(0) = ki/|I|,建立一个迭代过程来计算Q和CR。
-
最近,Liao等人提出了基于声誉再分配(IARR)的迭代算法,通过增强名誉用户的影响力来提高有效性。在迭代过程中,用户名誉的更新公式为:
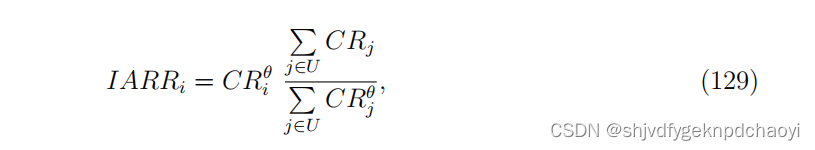
( 其中θ为可调参数,以控制声誉的影响。)
显然,当θ = 0时,IARR与AR法相同。
当θ = 1时,IARR退化为CR方法。 -
为了进一步提高该方法的可靠性,作者提出了一种先进的方法IARR2,在式(124)中引入惩罚因子,即:
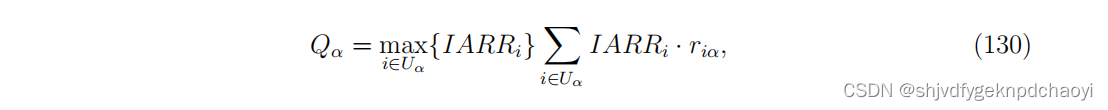 将式(129)中的CRi修改为:
将式(129)中的CRi修改为:
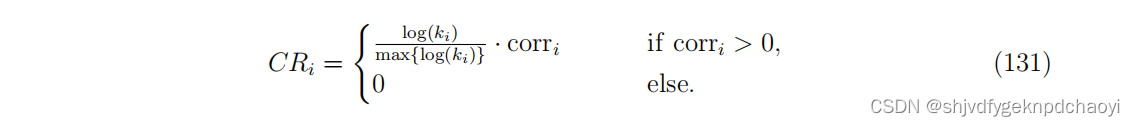
IARR2强调低口碑用户评价的商品通常质量较低,只评价了少量商品的用户不可能有高口碑。 -
BiHITS 及其变体
我们已经介绍了单部网络(节点属性为同一类) 的HITs算法,这里我们介绍了双部网络的HITs算法,称为“biHITS”。
- Ri和Fα分别表示用户i的声誉和项目α的适应度。
- 适应度衡量的是一个项目有多好,比如产品的质量或一篇科学论文的影响力。
考虑一个有向二部网络,biHITS可以写成:
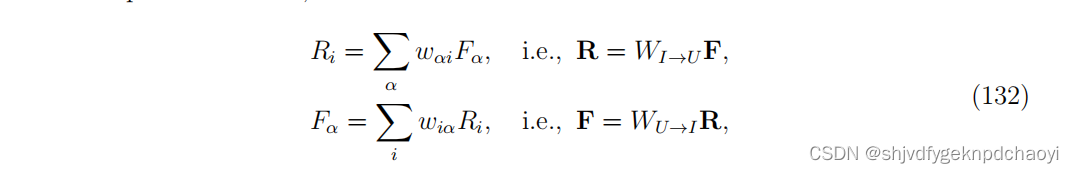
(其中W为二部网络的链接权矩阵(即加权邻接矩阵),R和F分别为用户声誉向量和项目适合度向量。)
对于无向网络,Wu→I = W(u→I)^T转置。可以通过下面的一组方程迭代求解:
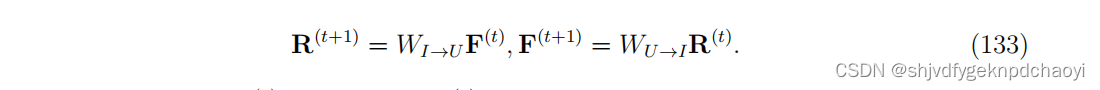
- 最初,可以令Ri^(0) = 1/√n和 Fα^(0) = 1/√m。注意,如果网络是连通的,则解是唯一的,与Ri(0)和Fα(0)的初值无关。
- 在每次迭代中,Ri和Fα都应归一化,使二范数:||r||2和||F||2 的值始终为1。
- 当R和F中所有向量元素的绝对变化之和小于一个极小的阈值ε时,迭代停止。
- 对于未加权的二部网络,可以将链路权重矩阵W替换为常规的邻接矩阵。
4.Algorithms with content information 包含内容信息的算法
- Deng等人提出了一种广义Co-HITS算法,将二部网络与来自用户端和项目端的内容信息结合在一起。
- 他们从不同的角度研究了两个框架,迭代框架和正则化框架。
(普通biHITS是在一定参数下的一种特殊情况。)
在这里我们简要介绍了迭代框架,其基本思想是通过一个迭代过程将分数传播到二部网络上,并从两方面进行约束。
为了将二部网络与内容信息结合起来,广义Co-HITS方程可以写成:
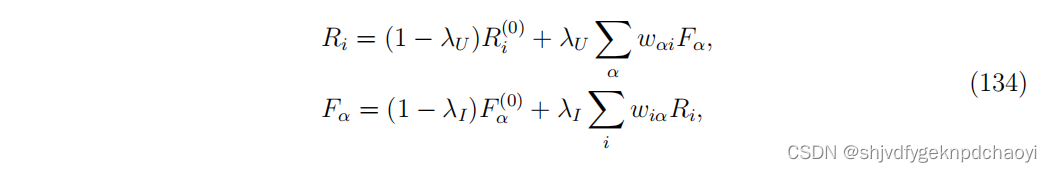
(其中,λU∈[0,1]和λI∈[0,1]为个性化参数。)
- 初始分数Ri^(0)和 Fα^(0)使用 文本关联函数f 计算,如向量空间模型和统计语言模型。
- 对于给定的查询q, Ri ^(0) = f(q, i)和 F^α (0) = f(q, α)。
- 当λU = λI = 1时,Eq.(134)退化为普通biHITS算法。
5.Algorithms with user trustiness 基于用户信任度的算法
biHITS的一个变体被称为QTR (Quality-Trust-Reputation),它考虑了从用户社会关系中提取的用户信任信息。
- 在用户网络中,如果用户i信任用户j或用户j的朋友,则会有一个从i到j的链接。链接权重用Tij表示,表示用户i信任用户j的程度。
考虑一个无向网络,QTR方法定义为:
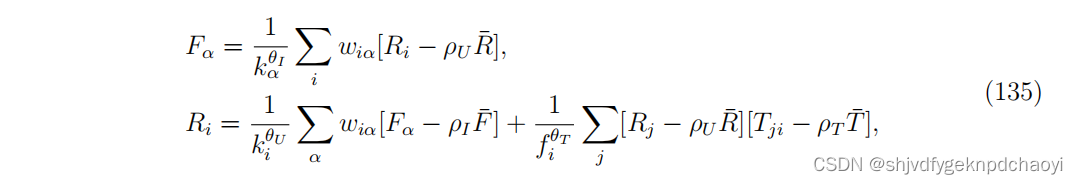
- fi是信任用户i的用户数量,F¯= Σα Fα/m,¯R = Σi Ri/n 和 T¯= Σ ij Tij/[n(n−1)] 分别为社团中:项目适合度,用户信誉和信任的平均值
- 6个可调参数,θU, θI, θT, ρU, ρI和ρT全部取值范围为[0,1]。
- 如果所有这些参数都为零,QTR降为普通biHITS。特别是,θI的两个边界选择对应于:通过对相邻用户的声誉求和(当θI = 0)或平均(当θI = 1)获得的项目适应度。
- θU和θT的意义是类似的。
- 相比之下,ρI决定与低适应度物品的交互是否会损害用户声誉(当ρI > 0时)(当ρI = 0时)
- ρU和ρT的意义是相似的。
- 对所有用户设置Ri^(0) = 1/√n,对所有项目设置Fα^(0) = 1/√m,迭代求解。
在步骤t + 1,更新用户信誉和物品适合度如下:
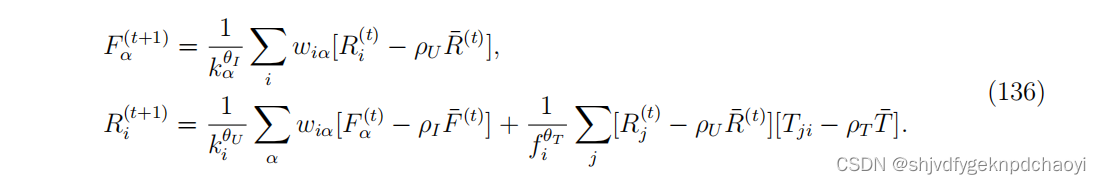
为了避免发散,在每一步中,Ri和Fα都应归一化,使R和F的二范数的值始终为1。
当算法收敛到稳态时,迭代过程停止。
实验结果表明,社会关系对提高排名质量具有重要作用。
6.Algorithms with the credit of item provider 基于物品提供者信用的算法
在许多评价系统中,除了考虑用户和物品的信息外,还考虑物品提供者的信用。
- 例如卖家都有一个信用评分,这是根据卖家获得的评级计算出来的。
当用户想购买一件只有少数人评价的新商品时,卖家的信用在很大程度上影响了用户的决定。
如果一件物品是由高信用的卖家出售的,那么它就会被认为是高质量的
同时,高质量的商品可以提高卖家的信誉。
这种说法也适用于描述作者和论文之间的关系。
- 具体来说,如果一篇论文被著名科学家(即高信用科学家)授权或引用,那么它就被认为是高质量的
同时,一篇高质量的论文可以提高作者的声誉,如Zhou等人提出的作者-论文二部网络的迭代算法。
- 基于这一想法,Fujimura等人提出了一种名为 “特征向量谣言” 的新算法,该算法基于特征向量,通过加权博主的hub和authority分数来量化每个博客条目。
在此框架下,存在两种二部网络,即用户-物品网络和提供者-物品网络。
如果我们把这两个二部网络结合起来,我们就得到了一个用户-物品-提供者三方网络。
在项目-提供者网络中,项目和提供者的度分别为dα和dm。
A表示provider的credit value的向量,eigenrumors算法:

- 其中ω是[0,1]范围内的一个可调参数,它决定了provider信用和用户评级对item适合度的相对贡献值
- 将两个矩阵W和P标准化,以减少对活动用户和提供者的bias。
- 将该方法应用于用户-论文-作者三方网络,并考虑到得分较低的实体的负面影响,提出了一种特征谣言的变体QRC (Quality-Reputation-Credit),即 :
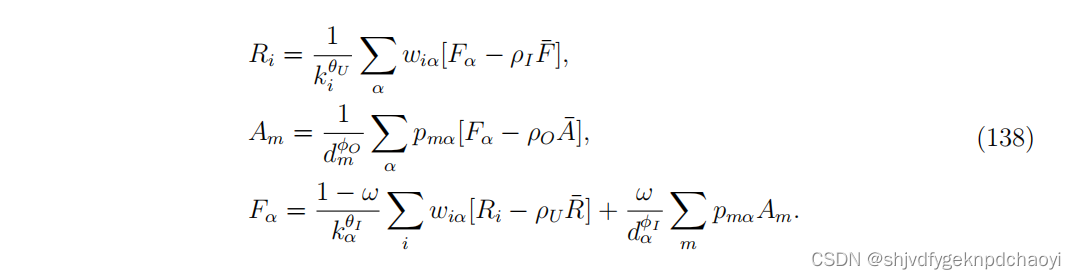
- kα和dα分别为项目在用户-项目网络和提供者-项目网络中的度数。
- φI和φO的意义类似于θU, ρO的意义 类似于ρU。
八、将对代表性方法进行广泛的实证分析,并在不同的网络和目标函数下展示它们的优点、缺点和适用性。
1.无向图
1.数据集
我们比较了八种代表性算法在四种无向无加权网络上的性能:
(1) Amazon是亚马逊网站上产品之间的联购网络。如果产品vi经常与产品vj共同购买,则在vi和vj之间存在无向边。
(2) Cond-mat是一个科学家合作网络,从1995年1月1日到2003年6月30日在www.arxiv.org上的预印本。在这个网络中,一个节点代表一个作者,如果两个节点共同授权了至少一篇论文,则连接两个节点。很明显,每一个预印本都会形成一个小团体,其中作者是完全联系在一起的。
(3) 电子邮件-安然Enron是一个包含约50万封电子邮件的通信网络。每个节点都是一个唯一的电子邮件地址。如果邮件从地址vi发送到地址vj,则在vi和vj之间存在一条无向边。
(4) Facebook是从facebook.com提取的友谊网络,其中节点表示用户,边(vi, vj)表示用户vi和vj是朋友。
基本统计特征如表2所示。

2.结果
- 为了评价排序方法的性能,我们研究了不同排序方法的排序得分与通过模拟网络上的扩散过程得到的节点影响之间的Kendall’s tau相关系数τ。(τ越高表示性能越好。)
在易感感染-恢复(SIR)扩散模型中:
- 除受感染节点(即初始种子节点)外的所有节点最初都是易感的。
- 在每个时间步中,每个受感染节点将以β的概率感染它的每个邻居节点。
每个感染节点以一定概率(µ)进入恢复状态。(为了简单起见,我们设µ= 1。) - 当不再有任何受感染的节点时,传播过程结束。
定义初始种子的传播影响为恢复节点数。
1.节点与传播影响
表3给出了算法得到的排名分数与SIR扩散模型得到的真实扩散影响之间的Kendalls tau相关系数τ。
对于每个网络,感染概率设为β = 1.5βc,其中βc为approximate epidemic threshold(近似流行阈值):
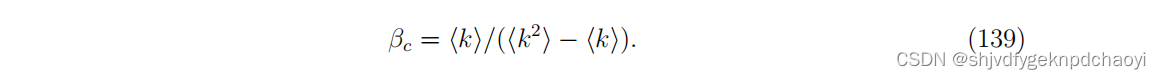
从结果中:
- 可以看到LocalRank和eigenvector centrality特征向量中心性的表现总体上比别人好。
(LocalRank是5个local centralities中表现最好的,后者在4个global centralities中表现最好的。) - 在某些网络中,LocalRank甚至比某些全局方法更好。
- 中间度(Betweeness),因为中间度值高的节点通常是连接两个社区的桥梁,可能没有很高的传播影响力。
- 与degree相比,coreness and H-index在这四个网络中都有较好的表现。
2.节点对网络连通性的重要性
除了传播影响,我们还研究了节点对网络连通性的重要性。
每种方法根据节点的 importance score 给出一个节点的 rank list。
然后,我们逐一去除排名最高的节点,计算每次去除后的(giant component)巨型分量σ的大小。
显然,σ随着移除节点数量的增加而减小,当节点的关键部分(pc)被移除时σ消失,见图11(a)中的示意图和图11©中Facebook上四个中心的结果。
为了找到pc的确切值,我们研究了节点移除后网络的磁化率值S:

(其中,ns是大小为s的组件的数量,n是整个网络的大小。)
通常,在网络崩溃(即网络分解为许多较小的不连接的片段)的关键部分pc处存在一个峰值S,如果节点移除过程中网络多次崩溃,则存在多个峰值。
pc值由最大值决定。pc越小,排序算法越好。
- 鲁棒性是量化排序方法性能的另一种度量。
它被定义为σ - p曲线下的面积,数学上是这样理解的:
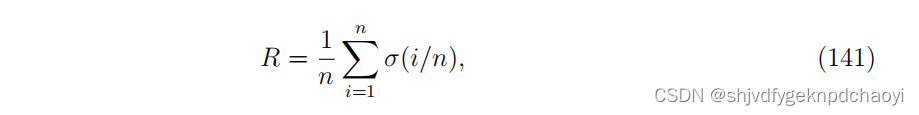
(其中σ(i/n)为从网络中去除i/n个节点后的巨型分量的大小。R越小,算法越好。)
不同方法在四种真实网络上的鲁棒性R和pc分别如表4和表5所示。
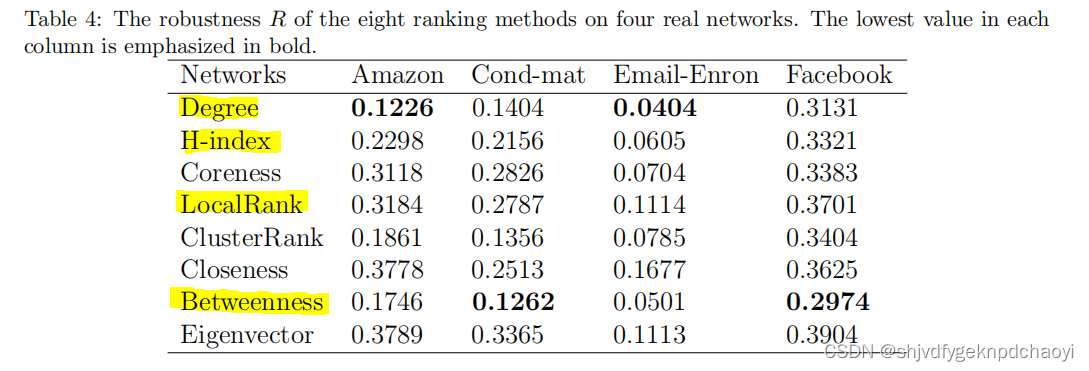
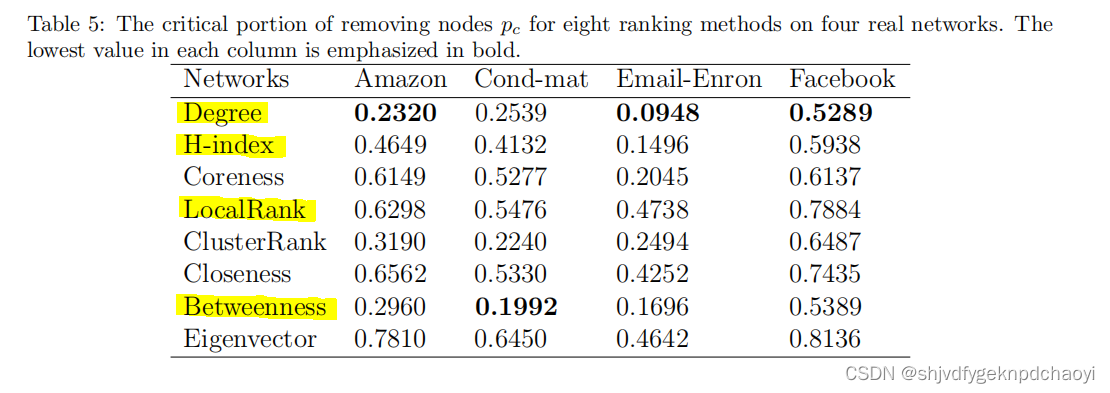
从结果中:
- degree度节点的性能最好,说明高度数节点对网络连通性非常重要。
- H-index和LocalRank方法也可以给出相对较好的结果。
- 中间性Betweenness是四个全局中心中最好的方法,通常会得到第二好的结果。
2.有向图
1.数据集
使用四个有向网络来测试第2章和第3章中介绍的六种方法的性能:
(1) Delicious 是一个从网站delicious.com中提取出来的有向社交网络,用户的主要功能是收集 useful bookmarks with tags。
- 用户可以选择其他用户作为他们 opinion leaders of web browsing浏览网页的意见领袖,因为这些意见领袖的 bookmarks 通常是有用和相关的。且用户可以自动订阅领导书签。
当然,选择自己领导者的用户也可以反过来成为其他人的领导者。 - 这样,用户就形成了一个大规模的有导向的社交网络,信息从领导者流向追随者。
链接的方向总是从一个追随者到他的领导。
(2) email - euall 由欧洲一家大型研究机构2003年10月至2005年5月的电子邮件数据生成。
给定一组电子邮件消息,每个节点对应一个电子邮件地址,如果vi至少收到一封来自vj的电子邮件,则存在从节点vi到vj的有向链接。
(3) Epinions 是一般消费者评论网站Epinions.com的“谁信任谁”在线社交网络。
-
网站成员可以决定是否“信任”彼此。所有信任关系相互作用,形成信任网络,然后与评论评级相结合,以确定哪些评论可以显示给用户。
-
如果vi信任vj,则存在从节点vi到vj的有向链接。
(4) wikipediagervote网络 包含从维基百科成立到2008年1月的所有维基百科投票数据。
网络中的节点表示维基百科用户,从节点vi到节点vj的有向链接表示用户vi投票给用户vj。
这四个网络的基本统计特征如表6所示。

2.结果
我们还考虑了SIR扩散模型,以评估算法识别具有高扩散影响的重要节点的性能。
在有向网络中,信息(或流行病)沿有向链路传播。
算法给出的排序分数与SIR模型得到的真实扩散影响之间的kendall tau相关系数τ如表7所示。

- 由于各种方法在四种网络上的性能差异很大,很难说哪种算法是最好的。
- 一般来说,这三种局部方法的性能优于其他三种全局方法。
- 在这四个网络中,LeaderRank都比PageRank好。
为了评估节点对网络连通性的重要性,我们研究了节点移除后有向网络中的(weakly
connected component)弱连接组件。
不同方法在四种网络上的鲁棒性R和临界部分pc分别如表8和表9所示。
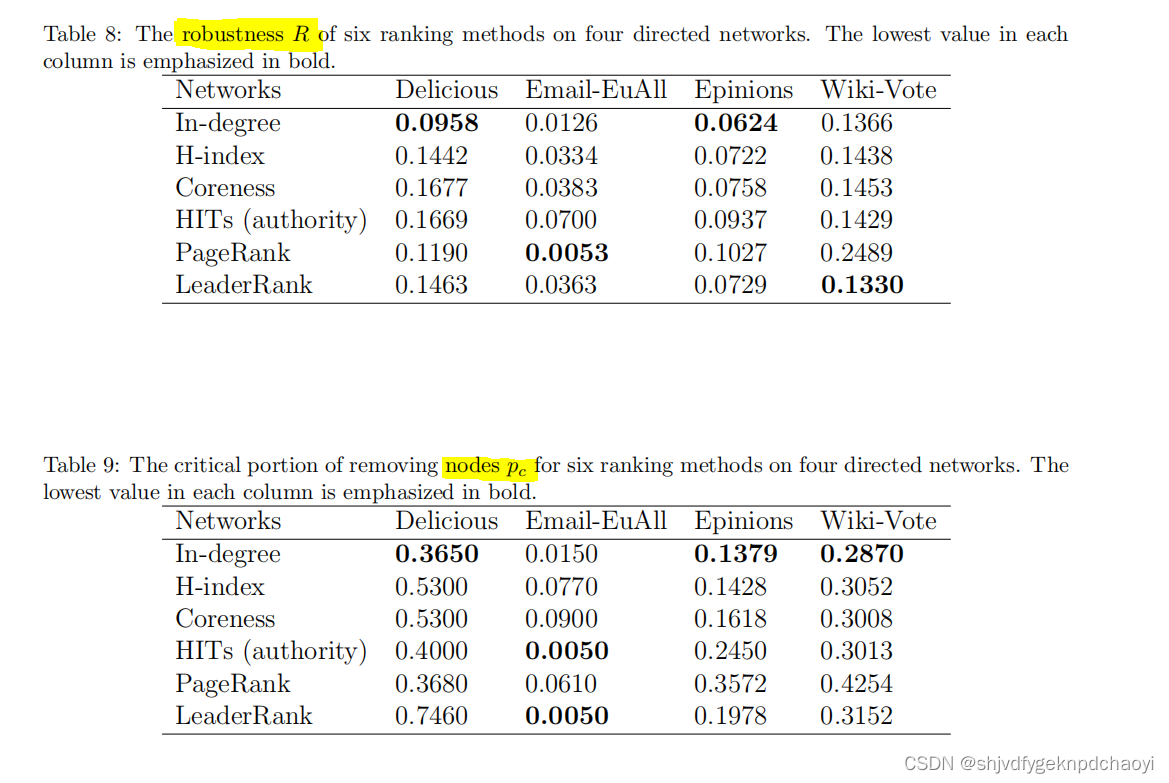
可以看出,网络在受到程度中心性攻击时更加脆弱。
注意,在某些网络中,R和pc表示的结果略有不同。
例如,在Delicious中,in-degree的R值最低,而in-degree的pc值大于PageRank和LeaderRank。
总的来说,in度是有向网络中节点重要性的一个很好的指标。
3.在加权图
1.数据集
采用4个加权网络对7种加权排序方法进行评价,包括2个有向网络和2个无向网络。
(1)青少年健康是根据1994 - 1995年进行的一项调查创建的定向网络。
- 每个学生被要求列出他/她的5个最好的女性朋友和5个最好的男性朋友。
- 一个节点代表一个学生,从节点vi到vj的有向链接表示学生vi选择学生vj作为朋友。
- 更高的链接权重意味着更多的交互。
(2)美国机场是2010年美国机场之间的定向航班网络。
每个链接表示从一个机场到另一个机场的航空公司,链接的权重表示该连接在给定方向上的航班数量。
(3)钦定版《圣经》是一个无向网络,包含钦定版《圣经》的名词、地点和名称以及有关它们发生的信息。
- 节点表示上述名词类型之一,边表示两个名词同时出现在同一诗句中。
- 边权值表示两个名词同时出现的频率。
(4)Cond-mat是第9.1节介绍的协作网络的加权版本。
- 如果k位作者共同授权了一篇论文,这k位作者中的任何两位之间的每条边都加1/k分。
- 对于每个网络,我们用边缘权值的最小值归一化,即从[wmin, wmax]到[1,wmax wmin],其中wmin和wmax分别是原始网络边缘权值的最小值和最大值。
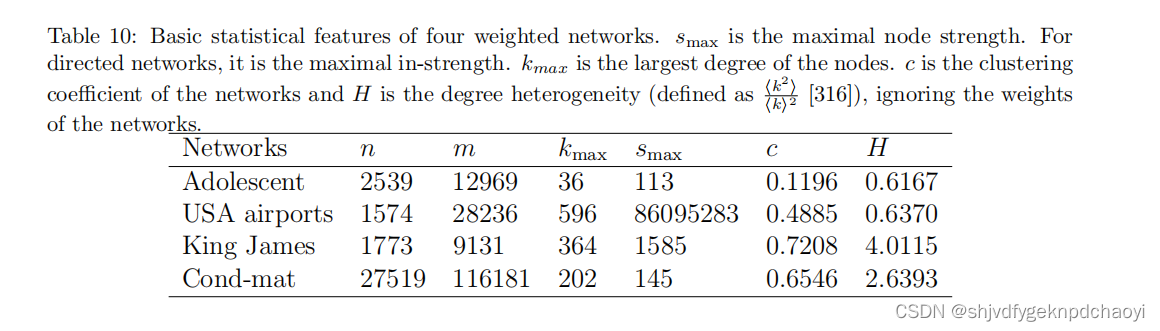
四个加权网络的基本统计特征如表10所示。
(度异质性H的定义与我们在9.1节中介绍的相同。)
2.结果
在加权网络中,SIR模型的扩展过程与未加权网络中的扩展过程相似。唯一的区别是,感染概率不是常数,而是取决于边缘权重。
Yan等人通过spreading rate传播率定义了感染传播:
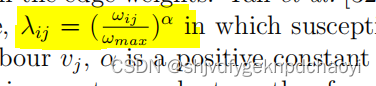
(易感节点vi从其受感染的邻居vj获得感染,α是>0的常数,ωmax是网络中wij的最大值。)
- 我们采用了另一种感染传播形式:受感染节点vi感染其易感邻居vj的概率为1−(1−β)^ wij
(wij是边(vi,vj)的权重。)
表11显示了算法给出的排名得分与SIR模型获得的实际传播影响之间的Kendalls-tau相关系数τ
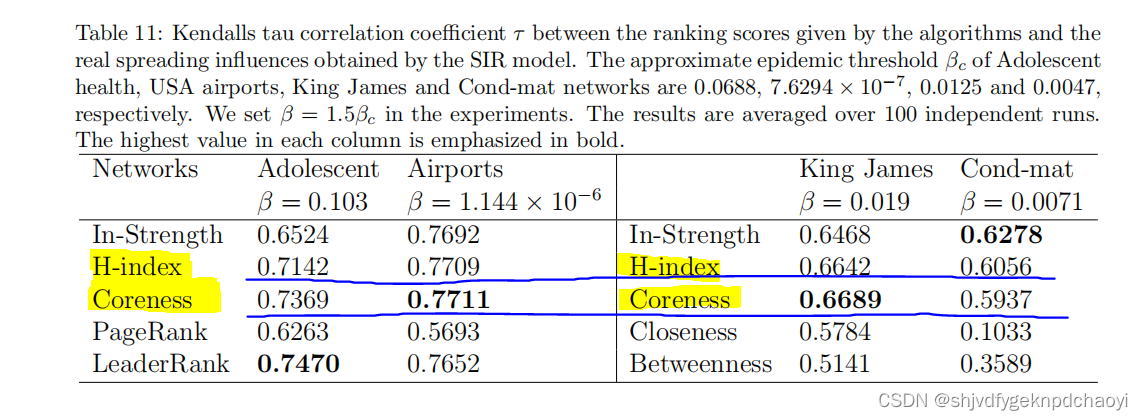
结果:
- H指数和核心度在识别有影响力的传播者方面具有优势,并且比某些全局方法表现得更好。
- 在两个定向网络上,LeaderRank优于PageRank。
网络连接性的分析与未加权网络中的分析相同。
七种方法在四个加权网络上的鲁棒性R如表12所示。
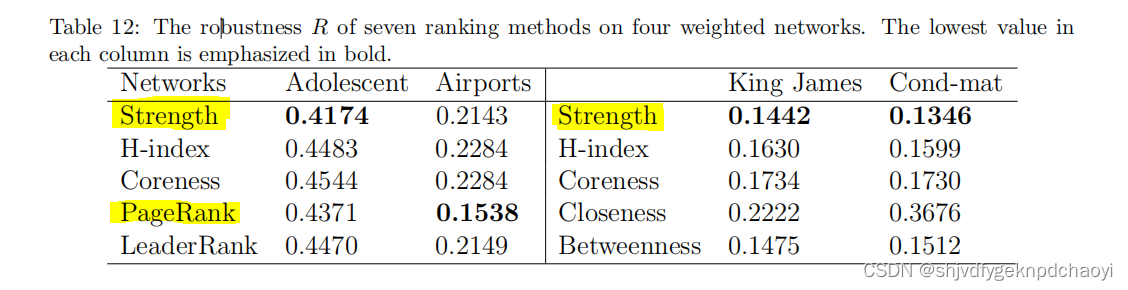
结果:
3. 与促进信息传播不同,为了保持网络连通性,strength表现优于加权H指数和加权核心度。
4. 事实上,strength在三个网络中表现最好,(除了Airports),Airports排名第二。
5. PageRank在机场数据集上表现最好,在两个有向网络上PageRank都优于LeaderRank。
6. 而在两个无向网络上Betweenness优于Closeness。
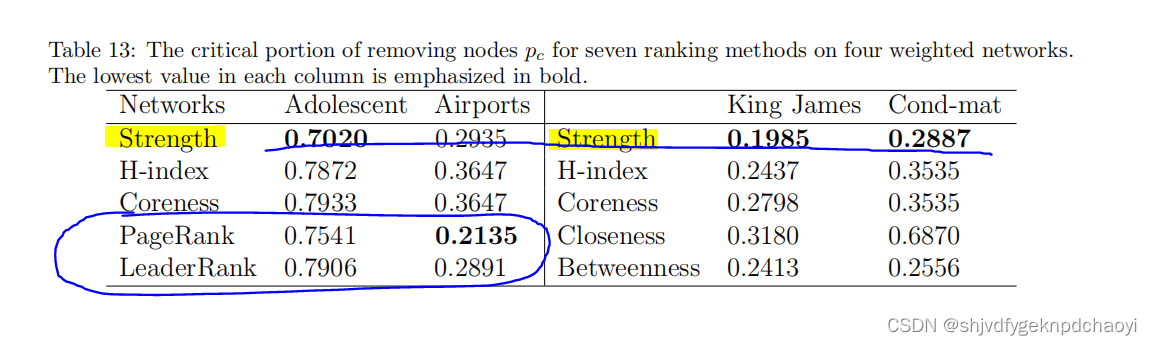
表13列出了移除节点pc的关键部分。获得了类似的结果。
同样,strength节点强度法的pc在大多数情况下是所有排名方法中最小的。
4. 在二部图上
1.数据集
在本节中,将在两个真实网络和一个人工网络上详细比较六种基于评级的排名算法。
(1) Netflix是DVD租赁公司Netflix于2006年发布的著名数据集的随机选择子集。
- 评级采用1至5的整数评级等级。
(2)MovieLens由GroupLens Research从MovieLen网站收集。
- 数据集的评分为0.5到5,步长为0.5。
- 所有选定的用户都至少对20部电影进行了评分。
- 为了测试第8章中算法的有效性,这两个数据集中所有获得奥斯卡最佳影片提名的电影都被作为基准。
(3)此外,在评级系统的演变过程中,通过优先附加机制,生成了一个由6000名用户和4000个项目组成的人工网络。
- 假设每个项目都有一定的真实内在质量,每个用户都有一定程度的评级误差。
项目质量Q在区间[0,1]上遵循均匀分布,用户的评级误差δ在区间[0.1,0.5]上遵循均匀分配。 - 用户和项目之间的评级关系是根据优先附加机制生成的。
用户i给出的项目α评级为:riα=Qα+δiα
(其中δiα来自正态分布[0,δi]。)
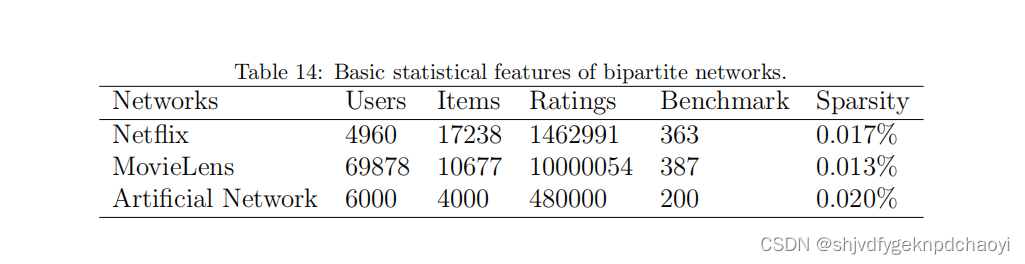
表14总结了三个数据集的属性,包括用户数量、项目、评级和基准项目,以及网络稀疏性。
2.结果
评估二分网络排名准确性的常用度量之一是AUC(接收机工作特性曲线下面积的缩写)。
AUC最初用于判断信号检测理论中预测方法的辨别能力。
计算排名算法AUC的一种简单方法是比较其对好项目和坏项目的辨别能力。
对于Netflix和Movielens数据集,将分别从基准项目(即获得奥斯卡提名的项目)和其他项目中随机选择两个项目。
根据排名算法给出的质量值,如果基准项目的质量高于另一个,则AUC增加1。如果两个项目获得相同的质量值时,AUC增加0.5。如果基准项目获得的质量低于另一个项目,那么AUC保持不变。
AUC的最终值将通过比较次数进行归一化,数学读数如下:

(其中n是比较次数,n’ 是基准项目具有比其他项目更高质量的时间,n’'是基准项目与其他项目具有seam qualities(接缝质量)的时间。)
对于人工网络数据集,将选择获得最高5%质量值的项目和评级误差属于最低5%的用户作为基准。
AUC检测排名算法区分好坏项目的能力,而皮尔逊积矩相关系数r用于测试所有项目的排名准确性。皮尔逊系数r反映了项目的某些真实内在质量与排名算法给出的评分质量之间的线性关系程度。
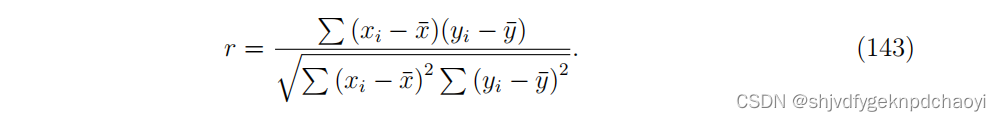
显然,皮尔逊系数r也可以用来根据用户的真实内在声誉和评分声誉来测试排名算法的准确性。
我们还测试了算法的抗攻击能力。
本节中考虑了两种攻击:
(1)随机评级:攻击者将以随机允许分数对项目进行评级。
(2)推送评级:攻击者将以最大或最小允许分数对项目进行评级。
从我们的实验中,我们发现IARR和IARR2中的参数θ非常敏感,必须谨慎选择。
Netflix和MovieLens排名算法的AUC如表15所示。

与所有其他算法相比,θ=1的IARR2在Netflix和MovieLens中表现最好。IR在Netflix表现相对较好,而CR和IARR在Movielens表现相对较好。
然而,很难说哪一项(例如电影)是最好的,应该被视为测试特定场景中排名算法有效性的基准。因此,构建的人工网络中,每个用户都有真实的内在信誉,每个项目都有一定的真实内在质量。
表16全面比较了算法的辨别能力,以评估用户的信誉和项目的质量。
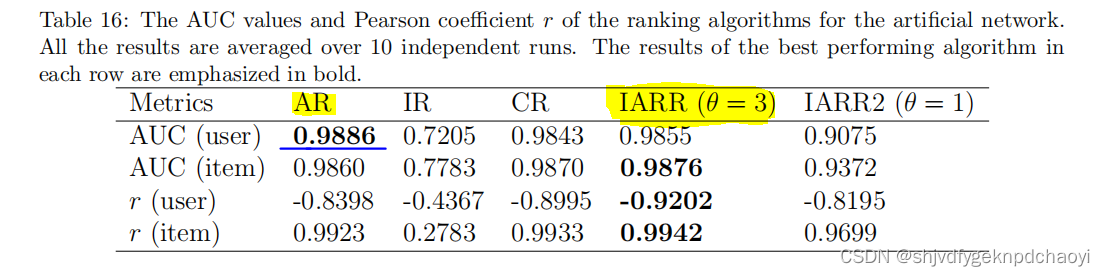
如上所述,AUC反映了排名算法的准确性,以区分普通用户或项目的好坏。因此,声誉最高的前5%用户和质量最高的5%项目被视为基准。
与真实数据集不同,这个人工网络中的评级不再局限于几个固定值。
因此,GR方法(根据用户的评级对用户进行分组)将不在此进行分析。
结果:
- AR在区分不同用户的影响方面表现最好
- θ=3的IARR表现最好
对于一个好的声誉评估方法,算法给出的用户最终声誉应该与其真实的内在声誉负相关。相关性越强,算法越好。
- 在所有用户的初始固有信誉的最小值和最大值之间定义了40个均匀分布的间隔,并将固有信誉落在相同间隔内的节点分组。代表性方法的结果如图12所示。
表17显示了**20%垃圾邮件发送者的不同算法(3种:随即攻击,推送攻击1&2)**的有效性。对于随机攻击策略,每个项目将获得[0,1]范围内的随机评级。
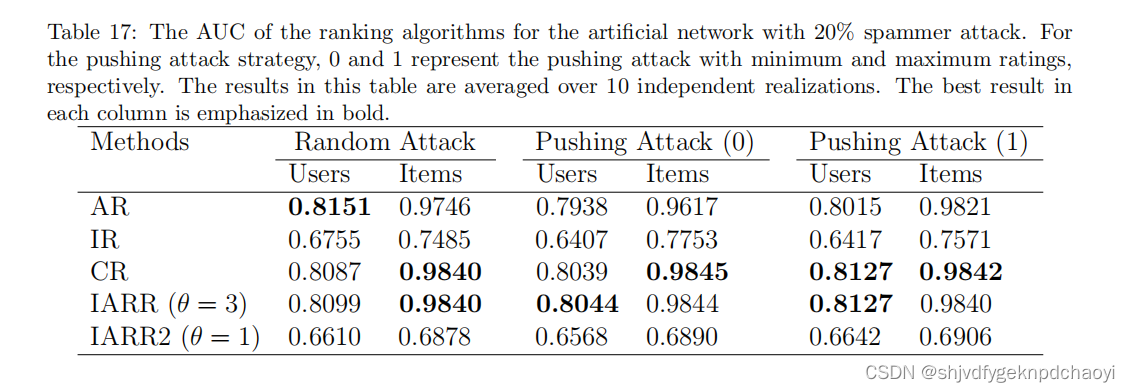
- 对于the pushing attack strategy 推击策略,每一项都会得到一个极值,即最低评级的推击为0,最高评级的推攻为1。
- 将分别选择具有最高内在质量的前5%项目和具有最低误差幅度的前5%用户作为基准。
结果:
- AR在对用户进行排名方面表现最好,CR和IARR在随机攻击下区分项目方面表现最好。CR和IARR也是推送攻击下最好的两种算法。
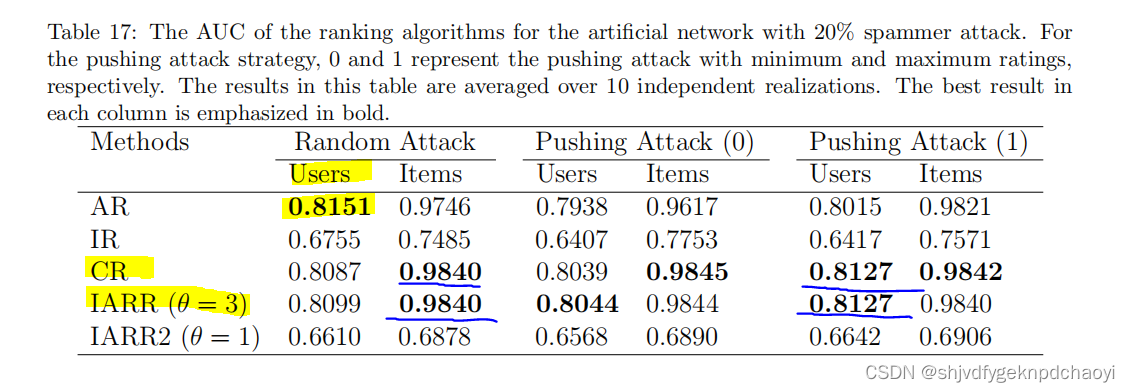
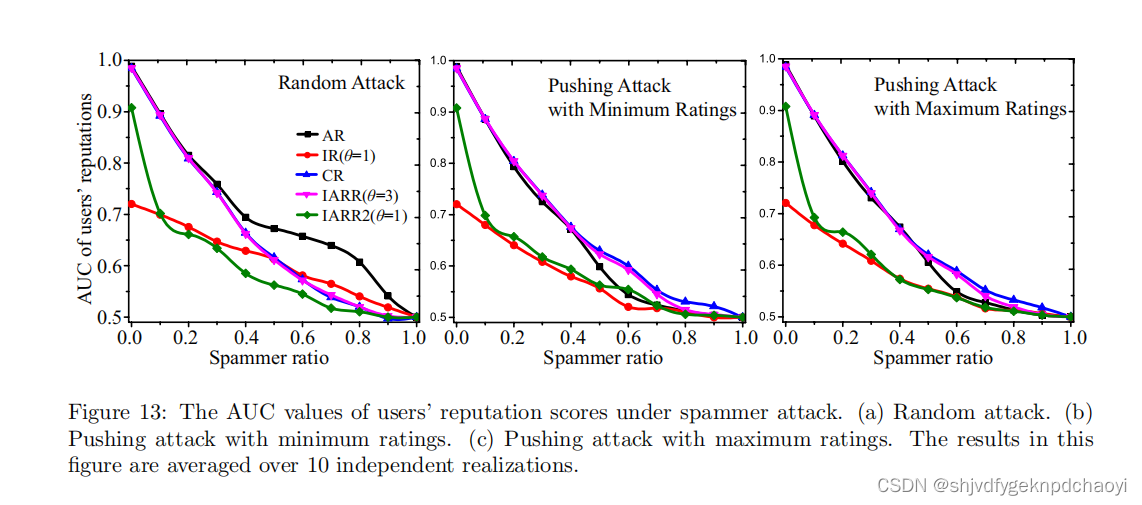
图13更清楚地说明了垃圾邮件发送者攻击下所有算法的有效性。
5.Finding a set of vital nodes 寻找一组重要节点
1.数据集
本节中使用的网络与第9.1节中的网络相同,即Amazon、Cond mat、Email Enron和Facebook。
为了评估算法找到一组有影响的节点的能力,我们还考虑了SIR模型。
最初,一组节点作为种子被感染,传播过程与我们在第9.1节中描述的相同。
然后,使用最终恢复节点的比率来衡量算法的性能。
我们测试了七种方法,包括度、介值、接近度、季氏渗滤法、胡氏渗滤法、CI和投票排名。
(degree, betweenness, closeness, Ji’s percolation method , Hu’s percolation method , CI and VoteRank )
对于两个参数相关的方法,我们为Ji方法设置L=0.05n,为CI设置L=2。
Ji和Hu方法的职业概率The occupation probabilities等于传播模型的感染概率。
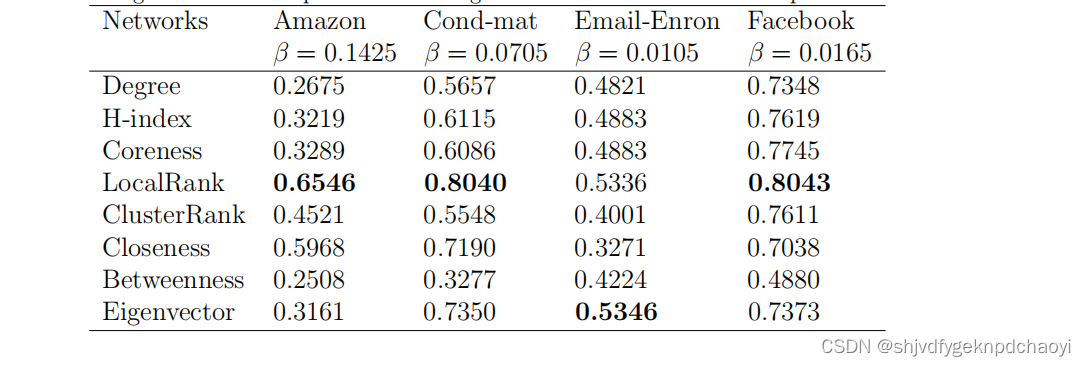
表18显示了通过初始化由不同方法选择的5%感染节点而触发的最终恢复节点的平均比率。
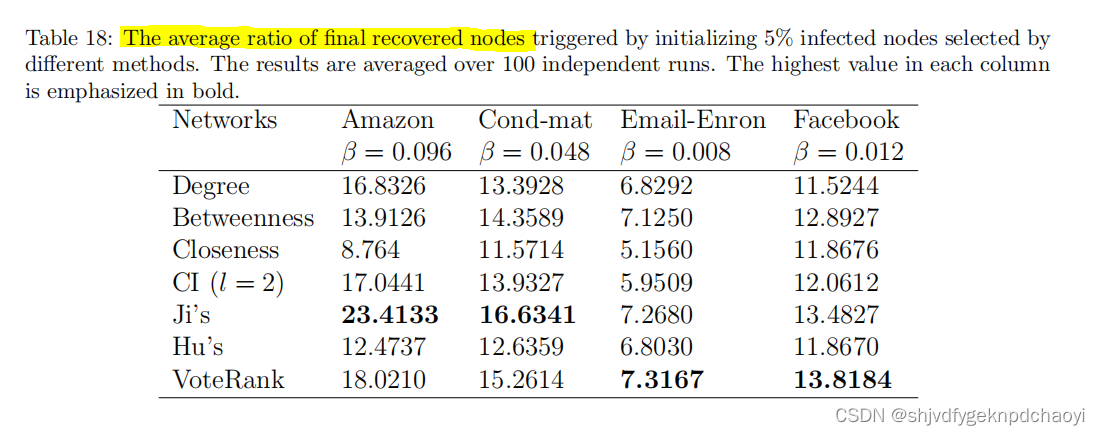
结果:
- Ji的方法和VoteRank具有相对更高的能力来找到一组高影响力节点以最大化信息覆盖。
- Hu的方法也相当好,而Closeness是最差的。
- 与查找单个节点的结果相比,Betweenes在查找一组重要节点方面并不差。
- 中间性Betweenness比接近性Betweenness表现得更好,这与查找单个节点的结果相反。
这可能是由于具有高紧密度值的节点通常紧密连接,导致高冗余,而具有高中间值的节点更可能分散分布。
为了研究一组节点对网络连接性的重要性,我们删除了一组网络节点而不是单个节点,以计算鲁棒性R和一致性S。
R和pc的结果分别显示在表19和表20中。
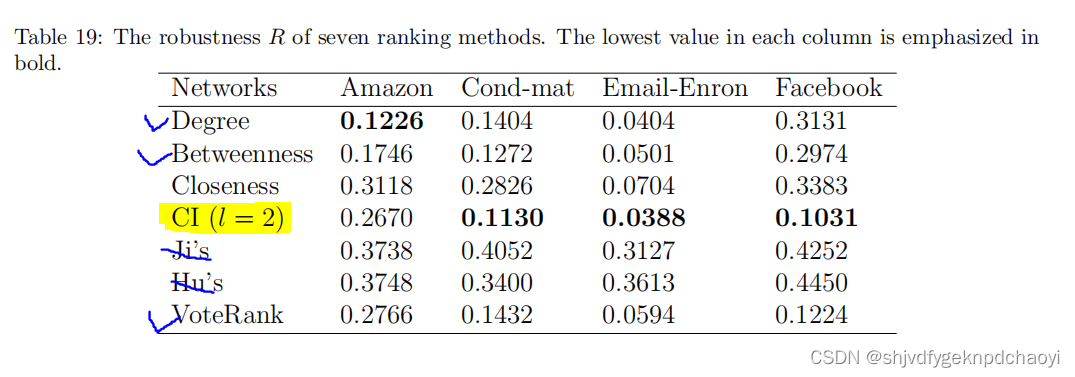
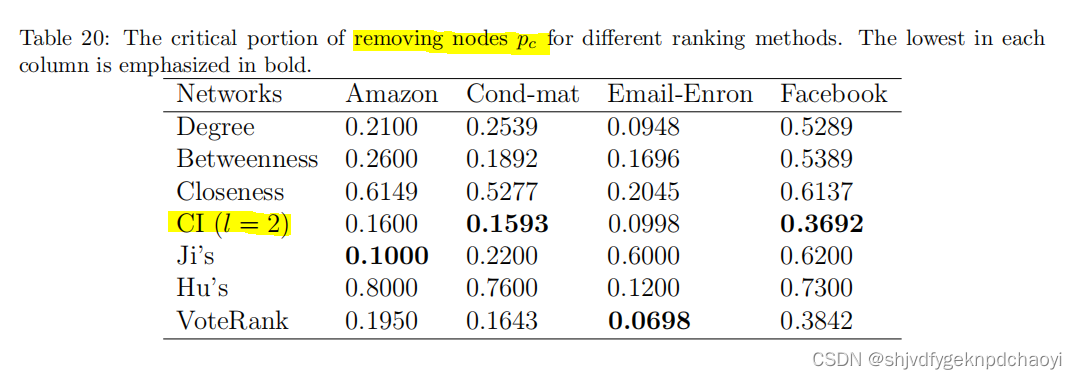
结果:
- 在大多数情况下,移除Ji和Hu方法选择的节点很难瓦解网络。
- CI方法表现最好,因为CI的最初目的是找到保证网络全局连接的最有影响力的节点。Degree、VoteRank和中间值也有相对较好的表现。
九、应用
1.识别社交网络中有影响力的传播者
谁是有影响力的传播者?它不仅取决于网络结构,还取决于所考虑的动态。 流行病动力学中的关键传播者在信息动力学中可能并不重要。
- Arruda等人研究了不同合成和真实世界(空间和非空间)网络中节点的传输能力与十个中心性度量之间的关系。
- 在非空间网络中的流行病动态中,核心性coreness和程度集中性degree centralities与节点的容量capacities of nodes最相关。
- 而在非空间网络中的谣言传播中,邻居的平均度、接近中心度closeness centrality和可达性accessibility表现最高。
- 在空间网络的情况下,可访问性accessibility在两个动态过程中都具有最佳的总体性能。
- 识别重要节点的算法广泛应用于社交网络。并且该应用程序通常可以在许多场景中带来一些可观的社会和经济价值,例如有影响力的传播者的虚拟营销,以及通过“免疫”重要人物来控制谣言。此外,它还可以帮助法医调查人员识别犯罪集团中最有影响力的成员,并监控诸如大规模动员等异常事件。
真正的实验很难在真正的在线社交网络上启动,因为不容易找到足够的参与者,也不容易通过将实验算法与已知基准进行比较来评估性能。因此,以前的大部分研究都是通过分析离线数据进行的。
然而,在珠海市中国移动公司的帮助下,我们进行了一些大规模的实验。
- 所考虑的网络是一个定向短消息通信网络,该网络在2010年12月8日至2011年1月7日的31天内使用消息转发数据构建。
- 每个节点代表由唯一移动电话号码标识的用户,**从用户vi到用户vj的链接意味着vi在这31天内至少向vj发送了一条短消息。**该网络包括9330493个节点和23208675个链路,其聚类系数仅为0.0043,最大程度为4832。
在我们的实验中,任务是找到一些具有较高影响力的初始用户。
3. 在第一步,我们根据不同的策略选择了1000个用户,例如选择LeaderRank得分最高的用户,或者排名最高的用户。
4. 其次,公司给他们每人发了一条信息。然后我们监控每种策略的转发次数。
5. 为了研究该算法对垃圾邮件发送者的弹性,我们删除了所有聚类系数为零的可能垃圾邮件发送者,然后在每个策略下选择1000个用户。
图14显示了两种策略(LeaderRank和度中心性)在两种情况下(有和没有垃圾邮件发送者)的直接转发数量分布。
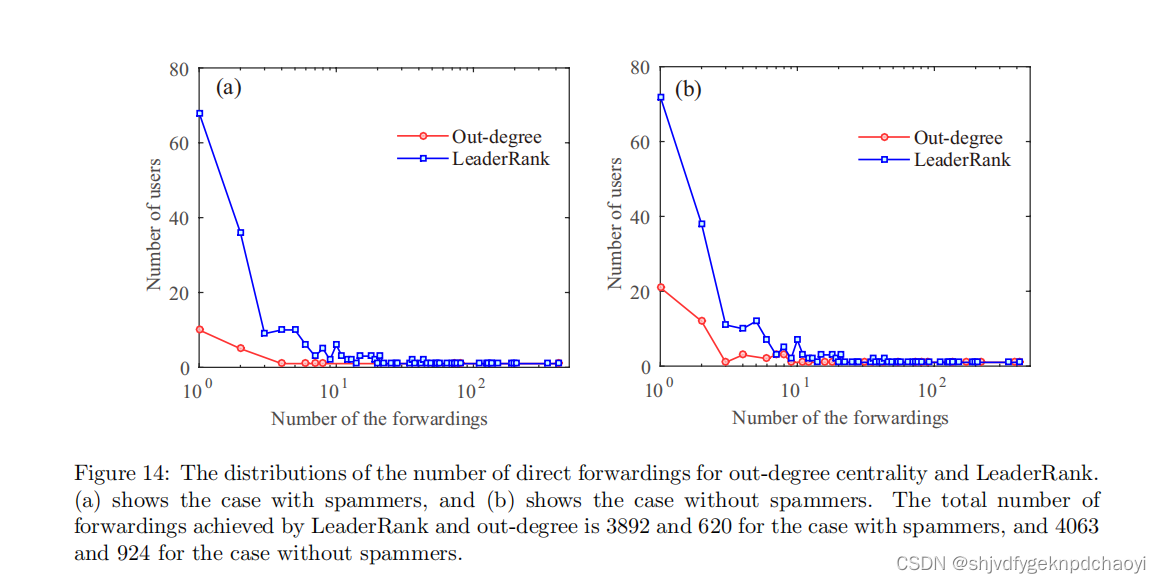
结果:
- 在垃圾邮件发送者的情况下,在按度外中心性out-degree centrality选择的1000个用户中,有22个用户至少转发了一次短消息,平均转发次数为28.18次; 删除垃圾邮件发送者的情况下,有62个用户至少转发了一次短消息,平均转发次数上升到31.03次。
- 对于LeaderRank来说,这种改善并不明显,这表明它对垃圾邮件发送者有很强的抵抗力。对于垃圾邮件发送者,在LeaderRank选择的1000个用户中,有207个用户转发了短消息,平均转发次数为18.8次。在没有垃圾邮件发送者的情况下,有221个用户转发了短消息,平均转发次数为18.38次。
- 尽管LeaderRank的平均直接转发次数低于度外中心性out-degree centrality,但在有垃圾邮件发送者的情况下,其总直接转发次数是超度中心度的6倍多,在没有垃圾邮件发送者的情形下是2倍多。
2.预测人体必需蛋白质
必须蛋白质的鉴定旨在创造具有最小基因组的细胞。
科学家通常将目标蛋白质相互作用网络的中心性度量centrality measures与生物信息相结合。
- 代表性方法包括:蛋白质-蛋白质相互作用梳理基因表达数据中心性(PeC)[339]、局部相互作用密度和蛋白质复合物(LIDC)[340]、将正交性与PPI网络相结合(ION)[341]、通过聚类系数加权的共表达(CoEWC)[342]、联合复合中心性(UC)[343]等。
蛋白质的重要性取决于:蛋白质邻居的数量以及蛋白质与其邻居共簇&共表达(co-clustered and co-expressed)的概率。
- LIDC将局部相互作用密度与蛋白质复合物相结合。
- ION是一种多信息融合方法,显示了同源信息在检测必需蛋白质方面的有效性。
- CoEWC捕获了数据中心和聚会中心的属性,尽管这两个中心具有非常不同的集群属性。
- UC是标准化α中心性和蛋白质复合物程度的组合。
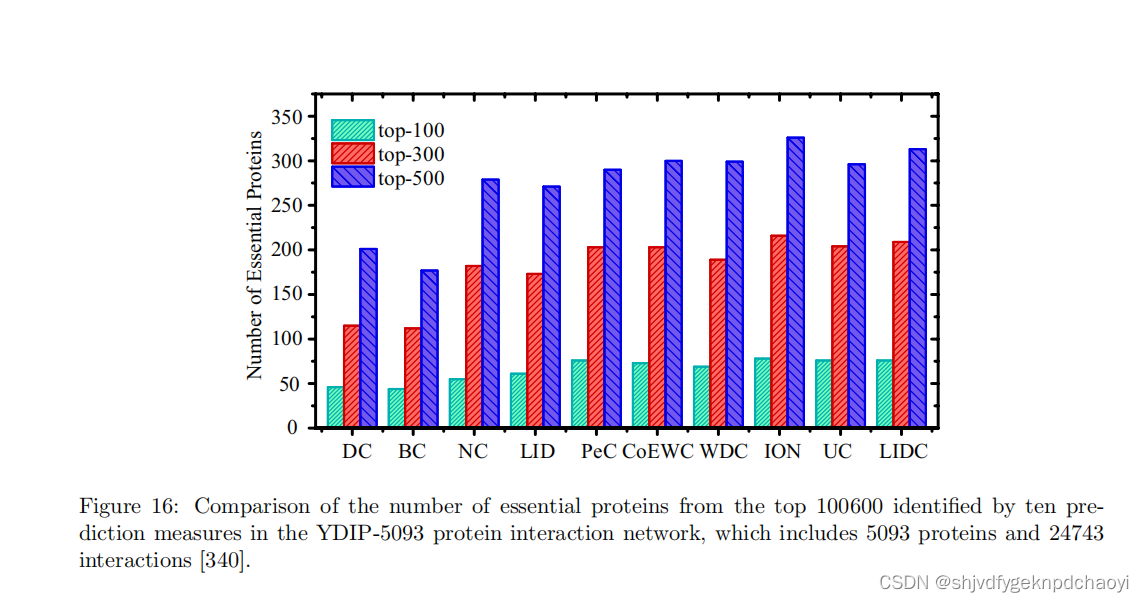
如图15所示,PeC的性能比仅使用拓扑信息(如度、距离、接近度等)的一些众所周知的中心性度量要好得多。
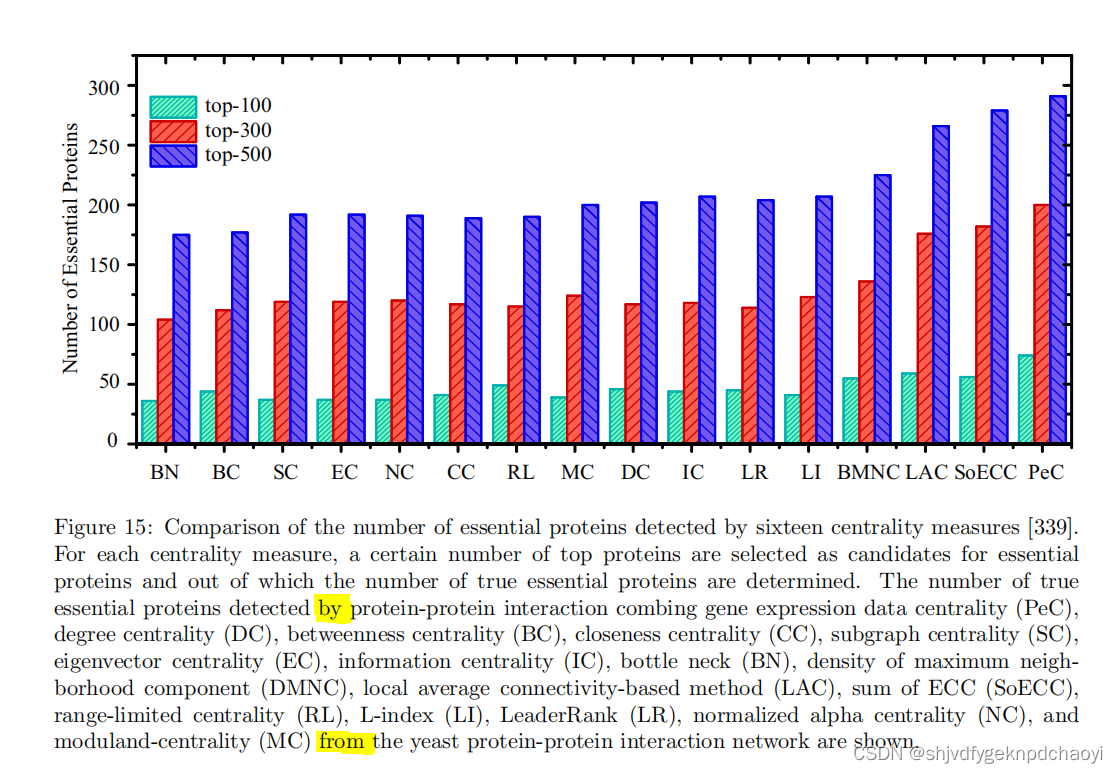
如图16所示,上述集成拓扑信息和生物信息的方法表现出相似的性能。
3.量化科学影响 Quantifying scientific influences
1.为了提供更精确的测量科学家影响力,一些研究人员借用了识别关键节点的概念,然后通过利用出版物和作者之间的各种关系提出了一些新的度量标准。
- 例如通过出版物之间的引用关系来量化出版物的影响
- 根据作者之间的引用联系对科学家进行排名
- 使用作者和出版物之间的多重关系来衡量科学家和出版物的影响。
- 通过使用引用关系,Chen等人基于1893年至2003年《物理评论》系列期刊中的所有出版物构建了一个引用网络。他们声称引用不能提供出版物影响的全貌,**因此假设如果出版物被许多重要出版物引用,则该出版物更重要。**然后,他们直接应用PageRank算法[92]。
- 基于相同的数据集,Walker等人[348]进一步考虑了抑制旧引用的时间衰减效应。为了利用这一因素,他们提出了一种名为CiteBank的新排名算法,该算法的灵感来自于浏览科学出版物的过程,研究人员通常从最近的出版物开始,然后随机行走。通过随机行走访问论文的概率被时间衰减函数ρi=e^(−agei/τdir) 降低,其中agei是出版物i的年龄,τdir是自由参数。
2.引文也可以用来衡量科学家的影响力,但不同的引文应该有不同的价值,**这取决于引用的科学家是谁。
从这个角度来看,Radicchi等人构建了一个作者对作者的引用网络(图17中显示了一个简单的例子)
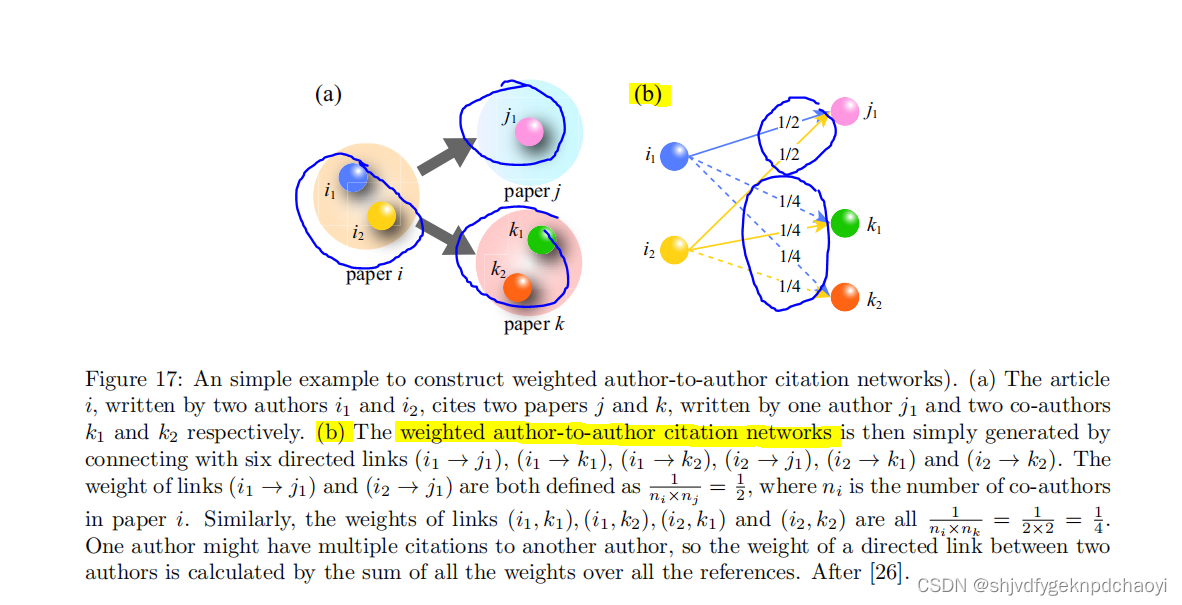
- 通过模拟科学学分(权重)的扩散,对科学家进行排名。
- 具体而言,Radicchi等人为每个作者分配了一个学分单位,并假设学分可以根据定向链接的权重按比例分配给其邻居。
- 换句话说,作者的信用评分取决于他们能从邻居那里获得多少信用。
- 所提出的算法基于一个迭代过程,该过程包括有偏随机游动和所有节点之间信用的随机再分配。
(1)有偏见的随机游走使得与排名较高的作者相关的链接比与排名较低的作者相关联的链接更为重要
(2)随机再分配考虑了科学学分传播的非局部效应。
3.考虑从作者到出版物的引用关系。
也就是说,如果作者i1和i2撰写的论文i引用了论文j,则将创建有向链接(i1,j)和(i2,j)。他们还考虑了作者和出版物之间的书面关系。因此,如图19所示,由两种关系组成的作者-出版物二分网络可以自然构建。
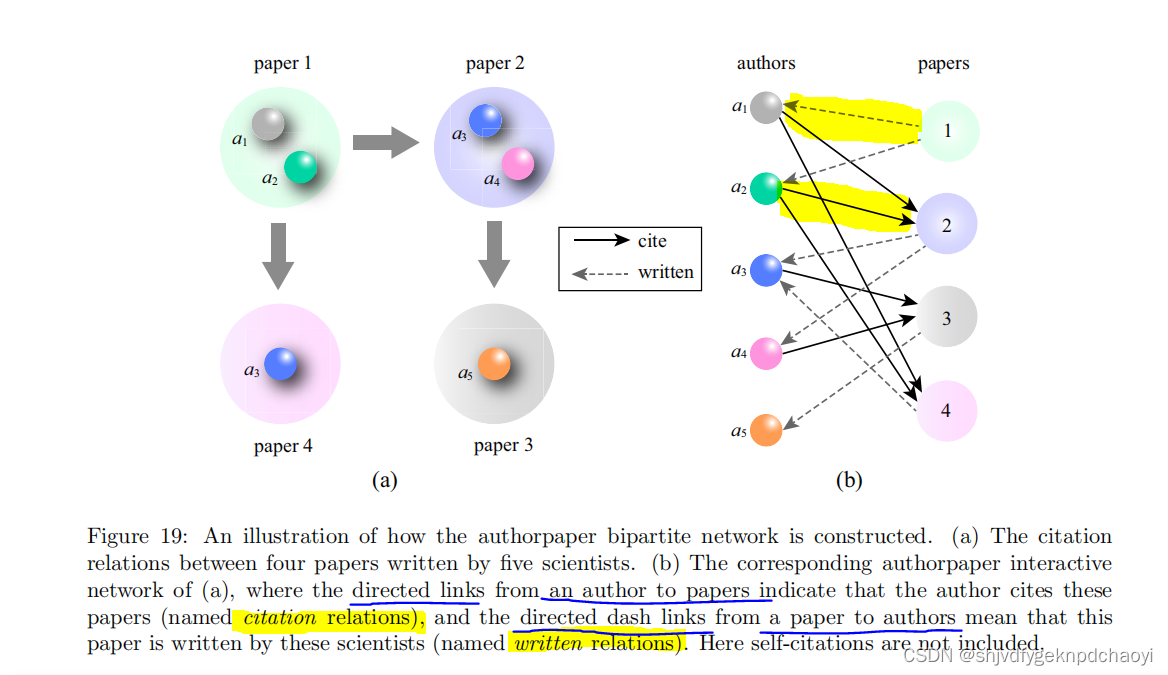
- 根据书面关系,每个出版物的分数将分配给其所有共同作者,这遵循质量扩散过程。
- 通过引用关系,论文分数的计算遵循投票模型,该模型将每位作者的分数添加到他/她引用的所有出版物中。
因此,基本假设显然是,当一篇论文被有名望的科学家引用时,它将具有高质量,而高质量的论文会相应地提高科学家的声望。
4.共同作者不同贡献
在上述申请中,出版物的所有共同作者的贡献被认为是同等重要的。然而,这一假设并不十分准确,并得到了一些讨论。例如,Stallings等人引入了一种公理化方法,**将更高的信用分配给具有更高阶的合著者。**这种为一个出版物分配学分的方法被称为A-index。