由于树状数组的数学原理证明是很复杂的，使用树状数组基本只需要知道它可以支持单点修改和区间查询即可。并且要知道，树状数组的作用是维护一段支持修改的区间和。

树状数组结构

下面是树状数组的图示：

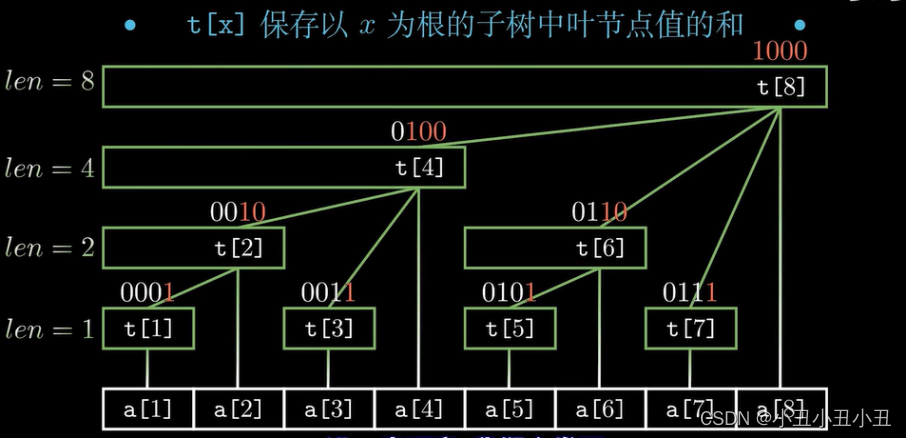
真正的数据是a[1]-a[8]这段数组。上面的tree数组是用来方便维护区间和的。
t[1]的lowbit是1，因此它的长度应该是1，所以t[1] = a[1]
t[2]的lowbit是2，因此它的长度应该是2，所以t[2] = t[1] + a[2]
t[3]的lowbit是1，因此它的长度应该是1，所以t[3] = a[3]
t[4]的lowbit是4，因此它的长度应该是4，所以t[4] = t[2] + t[3] + a[4]

…
依次类推下去，这就可以画出树状数组的结构图了。

单点查询为何这么写（不是数学证明）

关于单点修改，在图上的解释：比如我要在a[3]上加上常数K，那么我就必须要更新t[3]，t[4]和t[8].因为3以后的前缀和都会因为这次的修改而改变。
并且我们发现一个规律，**3 + lowbit(3) = 4, 4 + lowbit(4) = 8.**因此我们可以写出修改的代码了。

void add(int x, int v)
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}

区间查询为何这么写

关于区间查询，就是一个求前缀和的过程。由于我们刚刚说过的规律，当前下标 + lowbit(当前下标) = 下一个下标。 因此也可以写出对应的查询代码。

int query(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

上面就已经把基本的树状数组解释清楚了。现在开始用树状数组求逆序对了。

举个例子，比如现在有序列4321. 树状数组原序列为0000

1. 在位置4上的数字自增1，现在序列为0001，现在对应的逆序对是前缀和（4）-前缀和（4） = 0，对应的含义就是，当只有一个数字4的时候，逆序对个数为0
2. 在位置3上的数字自增1，现在序列为0011，现在对应的逆序对数量是前缀和（4）-前缀和（3） = 1，对应的含义是，当序列为43的时候，逆序对的数量是1
3. 在位置2上的数字自增1，现在序列为0111，现在对应的逆序对数量是前缀和（4）-前缀和（2）= 2 ，对应的含义是，当序列为432的时候，逆序对的数量是2
4. 在位置3上的数字自增1，现在序列为1111，现在对应的逆序对数量是前缀和（4）-前缀和（1）= 3 ，对应的含义是，当序列为4321的时候，逆序对的数量是3.
   5.3 + 2 + 1就是整体的逆序对数量，为6

这就是树状数组求逆序对的全部过程。

下面是对应的代码：（由于树状数组的数组下标从1开始，而输入的数据从0开始，所以全部让他自增1，并不会影响结果）

for (int i = 1; i <= n; i++) {
    int x = ++a[i];
    add(x);
    ans += query(n) - query(x);
}

最后ans就是逆序对的数量。