
一、说明
在这个世界上,会发生许多事件,其趋势可能遵循一种模式。在这篇博客中,我们试图为这些模式建模奠定基础。例如,在已经发生地震的地区,新地震的可能性通常会增加。这种可能性的增加主要是因为早期地震造成的余震。在一个国家/地区恐慌性抛售股票可能会导致另一个国家/地区发生类似事件。
以野火为例,今年亚马逊森林的野火可以大大减少来年另一场野火的发生。明年发生野火的可能性下降主要是因为现有森林燃料的燃烧。因此,很明显,类似事件的概率可以通过先前事件序列中的模式来增加或降低。
如果类似事件的概率提高,即每次发生都会增加未来发生的速率,就像地震的例子一样,那么这些事件可以归类为随机兴奋或自激发。如果类似事件的概率降低,如地震示例,那么这些事件可以归类为随机抑制或自我调节。如果类似事件的概率不受影响,则每次发生对未来发生的速率没有任何影响,则这些事件可以建模为泊松点过程
二、点过程理论
点过程是时间和/或空间中事件发生的随机模型。在这篇博客中,我们将强调点过程的纯时间方面,即点落下的空间只是代表时间的实线的一部分。
2.1 计数过程( N(t) )
首先,考虑一条表示时间和事件时间 T₁、T₂ 的线,...在沿直线下降的事件时间中,T i(事件时间)通常可以解释为第i 个事件的发生时间。此事件可以是特定地区的地震或亚马逊森林的野火。我们的工作是对这些事件时间进行建模。而不是对这些事件时间进行建模 T₁、T₂ ,...Tn,也可以用计数过程N(t)来描述。
计数过程 N(t) 可以看作是截至当前时间 t 之前进入系统的“到达”数量的累积计数。如果自安装地震仪以来的146年里,喜马拉雅山发生了80次地震,那么N(80)=146次。足够简单吧!
让我们也定义历史:H(u)到达时间u的历史。
2.2 条件强度函数 ( λ٭(t) )
当我们讨论随机性的概念时,定义一个函数是相关的,该函数给出事件在时间 t 发生的期望。该函数称为强度函数,表示为 λ٭(t),它表示事件预期在特定时间 t 附近发生的无穷小速率。 它以时间 t 之前点过程的先验历史 H(t) 为条件。

我们引入了诸如“自激发”和“自我调节”之类的术语,这些术语可以使用条件强度函数轻松理解。如果最近到达历史H(t)导致条件强度函数增加,则该过程称为自激发。一般来说,λ٭(t) 不仅取决于 t,还取决于前面事件的 Ti 倍数,即 H(t)。
当N为泊松点过程时,条件强度函数λ٭(t)仅取决于当前时间的信息,而不依赖于历史H(u)。泊松点过程既不是自激的,也不是自调节的。
λ٭(t) 只是泊松点过程随时间变化的函数,平稳泊松过程具有恒定的条件速率:λ٭(t) = α,对于所有 t。 λ٭(t) = α 意味着在任何时间点,事件发生的概率都是恒定的,无论此类事件发生的频率如何。
三、霍克斯Hawkes过程
霍克斯过程属于一个以它的创造者Alan G. Hawkes命名的自激点过程家族。自激励点过程模型是使用时间聚类的模型事件。像“地震”和“恐慌性抛售股票”这样的事件通常是在时间上聚集的,即事件的到来增加了在不久的将来观察到此类事件的可能性。让我们定义霍克斯条件强度函数 —
定义 {t1, t2, . . . , tk} 表示截至时间 t 的点过程过去到达时间的观测序列,霍克斯条件强度为

常数λ称为背景强度,μ(·)称为激发函数。如果μ(·)等于零,则此自激点过程简化为简单的平稳泊松过程。激励函数的常见选择μ(·)是指数衰减。
![]()
参数α和β是常量。α,β可以解释为系统中的每次到达都会立即将到达强度增加α,然后随着时间的推移,这种到达的影响以β的速度衰减。

修改后的霍克斯条件强度如下所示。幂律函数中另一个常用的激励函数。
α 和 β 是 λ٭(t) 的参数,设 θ 表示参数。点过程的参数向量 θ 是通过最大化对数似然函数来估计的。我们还可以使用参数函数来近似条件强度函数,我们将在本博客系列的下一篇博客中对此进行更多讨论。
自激点过程有一个明显的延伸,即互激点过程。这些本质上是一组一维点过程,它们激发自己和彼此。这组点过程称为多变量或相互激励的点过程。
如果对于每个 i = 1, . . . , m,则每个计数过程 Ni(t) 具有以下形式的条件强度:

四、模拟
让我们模拟一个简单的霍克斯点过程:λ:0.1,α:0.1,β:0.1,并尝试理解条件强度函数。

我们可以清楚地观察到上图中的激发和衰减。现在让我们将背景强度 λ 增加到 0.5。
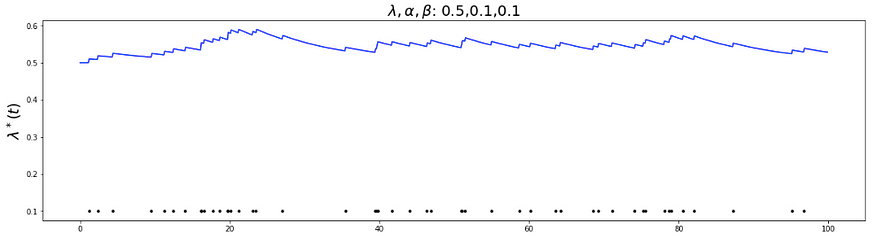
我们清楚地看到,随着背景强度的增加并徘徊在0.5以上,事件的数量也在增加。我们现在将尝试了解α的影响,β。让我们将α增加到 0.5。

我们可以清楚地看到,事件的数量增加了,这是因为事件的每一次发生都会使下一个事件的到达强度增加α。因此,λ٭(t)的增加变得更高,一个有趣的观察结果是λ٭(t)从0.1到0.6变化。
现在让我们将β增加到 0.5。请记住β控制事件的衰减率对其连续事件的影响。
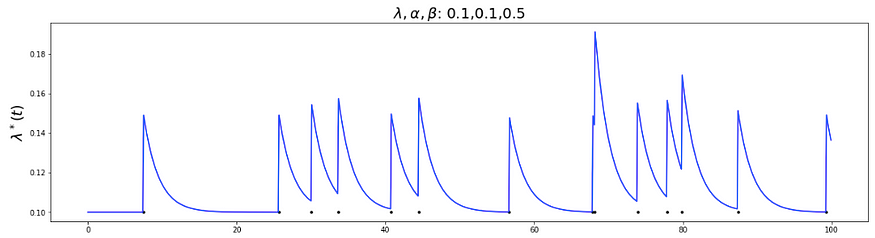
将此图与图1进行比较,图1中的衰减非常小于图4中的衰减。
霍克斯点过程的核心概念在上面的例子中得到了演示。
点工艺在各个领域都有广泛的应用。我们可以在连续的时间内对离散事件/事件的流进行建模。我们还可以使用函数近似,其中多个事件类型的条件强度函数可以通过像 LSTM 这样的新型神经架构来近似。在本系列的下一篇博客中,我们将讨论神经霍克斯过程。










![[用go实现解释器]笔记1-词法分析](https://img-blog.csdnimg.cn/img_convert/fd6c97651124c01e323e5360495f3f0e.png)

