文章目录
- 建立DH模型
- 机器人正运动学
- 机器人逆运动学
- 机器人雅可比矩阵
- △ 机器人速度雅可比矩阵
- ○ 雅可比矩阵相关概念
- ○ 以二连杆平面机器人举例说明雅可比矩阵
- △ 机器人雅克比矩阵与速度分析
- △ 雅克比矩阵的奇异性
- ○ 机器人的奇异位形(奇异形位、奇异点)
- △ 雅可比矩阵的建立
- ※ 相邻连杆间的速度关系
- ○ 矢量积法
- · 矢量积法概念
- · 矢量积法求机器人雅可比矩阵示例
- ○ 微分变换法
- · 坐标系的微分运动
- · 机器人的微分运动
- · 微分变换法概念
- ※ 关于相对于末端(工具)坐标系的雅可比矩阵
- · 微分变换法求2连杆机械臂雅可比矩阵示例
- ○ 矢量积法与微分变换法的转换关系
- △ ZK-500六轴工业机器人的雅可比矩阵
- ○ 矢量积法
- ○ 微分变换法
- ○ matlab机器人工具箱法
- · jacob0()
- · jacobn()
- · 雅可比矩阵的变换
- · matlab代码
CSDN提示我字数太多,一篇发不下,只好拆分开。。。
❤ 2023.8.2 ❤
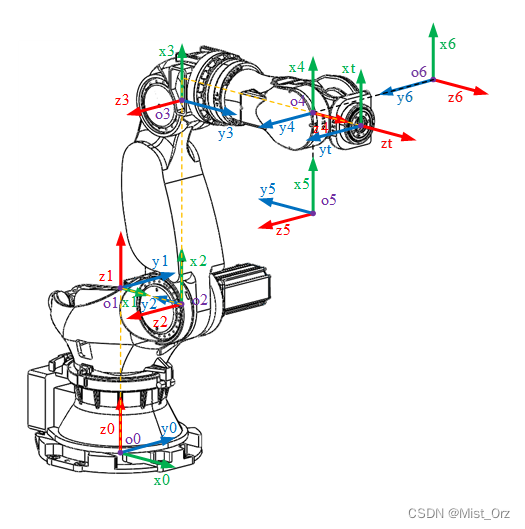
建立DH模型
→→→【工业机器人运动学与Matlab正逆解算法学习笔记(用心总结一文全会)(一)——DH模型与正运动学】
机器人正运动学
→→→【工业机器人运动学与Matlab正逆解算法学习笔记(用心总结一文全会)(一)——DH模型与正运动学】
机器人逆运动学
→→→【工业机器人运动学与Matlab正逆解算法学习笔记(用心总结一文全会)(二)——逆运动学P1】
→→→【工业机器人运动学与Matlab正逆解算法学习笔记(用心总结一文全会)(三)——逆运动学P2】
机器人雅可比矩阵
△ 机器人速度雅可比矩阵
关于雅可比矩阵的内容,说实话教材看得我一头雾水,感觉自己可能有阅读障碍综合征。。。。然后我在B站找到了这个教程,感觉很简洁实用
→→→【4-1机器人速度雅可比矩阵】
以下是我的学习笔记
○ 雅可比矩阵相关概念
- 雅可比矩阵概念
雅可比矩阵(Jacobian)是机器人操作空间速度与关节空间速度之间的线性映射关系,同时也可以表示两空间之间力的传递关系。
- 机器人末端位姿的表示
齐次变换矩阵
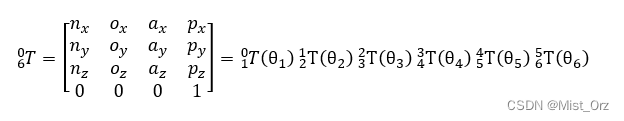
- 角度设定法
采用相对参考坐标系或相对运动坐标系作三次连续转动来规定姿态的方法
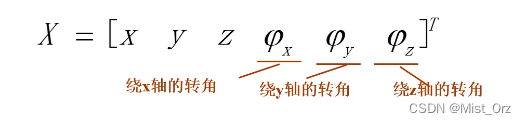
绕坐标系的转角正常来说就是欧拉角,是要考虑先后顺序的,但是这里的转角认为是与坐标轴的夹角

故用角度设定法表示机器人末端位姿时,机器人的运动学方程可写成
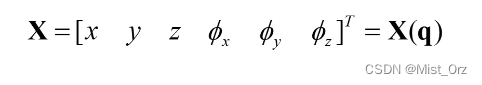
○ 以二连杆平面机器人举例说明雅可比矩阵
如图二连杆平面关节机器人
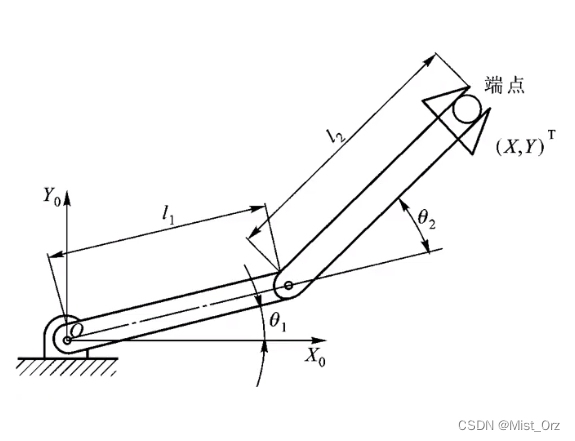
机器人末端位置可以表示为
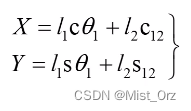
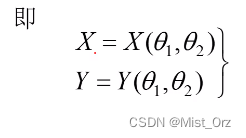
对改式求微分得
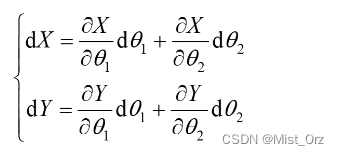

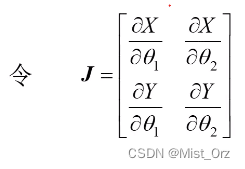
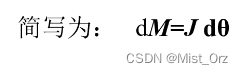
根据前面的式子可得
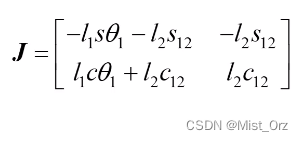
于是

△ 机器人雅克比矩阵与速度分析





- 每一列表示其他关节不动而某一关节运动的端点速度
- 前三行代表手部线速度与关节速度传递比;后三行代表手部角速度与关节速度传递比
- 雅克比矩阵J(q)是函数的一阶偏导数以一定方式排列成的矩阵,不仅可以用来表示操作空间速度与关节空间速度之间的线性映射关系,同时也用来表示两空间之间力的传递关系。
△ 雅克比矩阵的奇异性
在求机器人关节速度时,需要求雅可比矩阵的逆矩阵
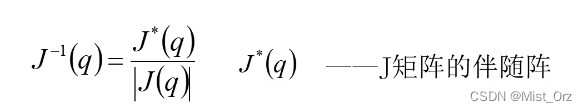
在一些位姿下,雅可比矩阵会出现行列式得0的情况,这是雅可比矩阵的逆矩阵就会趋近无穷

在计算机中由于数据存储方式,一般不会等于0,但是会出现一个很小的数,也认为其等于0.
○ 机器人的奇异位形(奇异形位、奇异点)


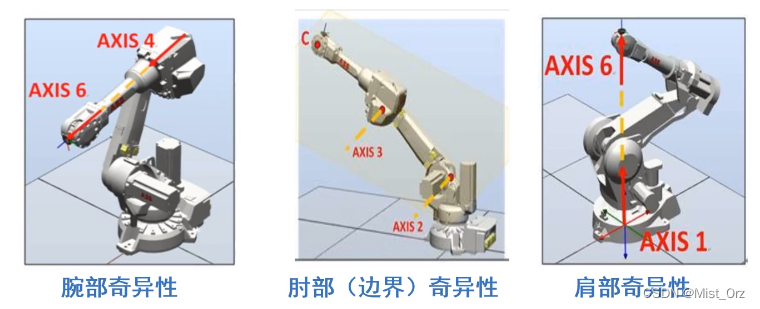
- 腕部奇异性:机器人4、6轴共线(5轴角度为0),造成四轴和6周大幅运动
- 肘部(边界)奇异性:机器人到达最大工作范围,造成肘部无法活动,3轴振动剧烈
- 肩部奇异性:1轴与6轴共线,或者1轴与4、5、6杆的坐标系原点共线,造成肘部大幅快速运动,容易造成危险
【待插入视频:工业机器人奇异性1】
→→→【工业机器人3种奇异点详解,没想到是先天缺陷,无法克服】
【待插入视频:工业机器人奇异性2】
→→→【【涨知识】机器人的奇异性是什么?】
△ 雅可比矩阵的建立

※ 相邻连杆间的速度关系
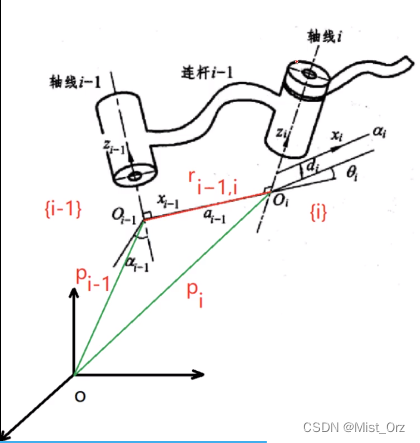
- 移动关节


- 旋转关节
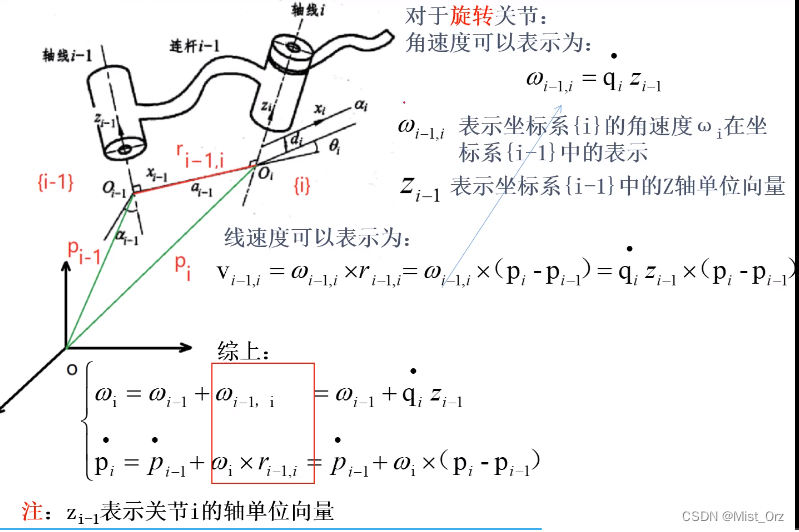
这部分我木有听懂,原视频链接在这里。。。
→→→【4-5机器人雅克比矩阵的建立】
○ 矢量积法
· 矢量积法概念
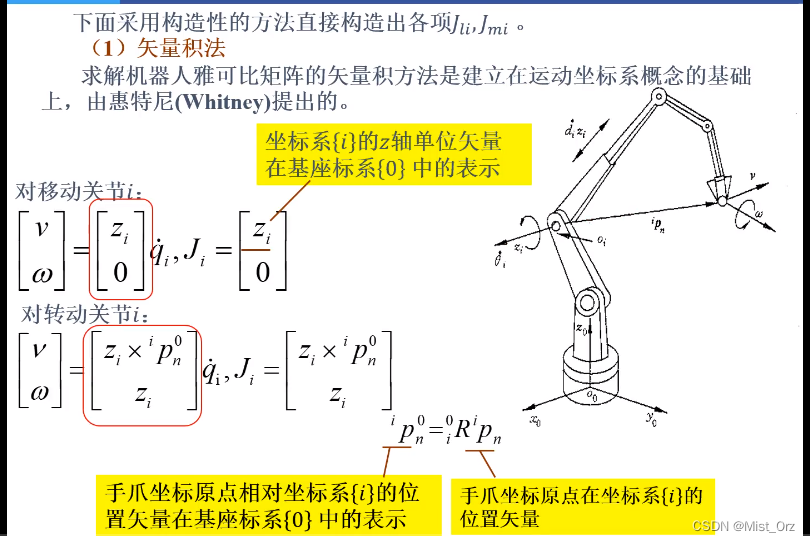

大概听明白了是什么意思(我自己的总结)
- 首先末端速度是各关节运动产生的速度的叠加
- 先假设某一个关节动,其他关节都不动,求出来这个关节的雅克比矩阵,也就是完整雅克比矩阵中的一列。
- 计算的重点就是求出这个旋转的半径,半径就是这个转动关节的原点到末端点的连线
- 每个关节都如此求解,最后把结果写在一起就是整体的雅克比矩阵。
【!注意!】
矢量积法求得的雅可比矩阵,计算后得到的速度向量是相对于基坐标系(世界坐标系)的
· 矢量积法求机器人雅可比矩阵示例
关于矢量积法求雅可比矩阵,之前的教程里没给出示例,这里还有一个视频可以参考
→→→【机器人学 l 3.6 速度雅可比矩阵的矢量积法】
- 首先视频讲了一下矢量积法的概念



- 矢量积法求平面2R机器人雅可比矩阵
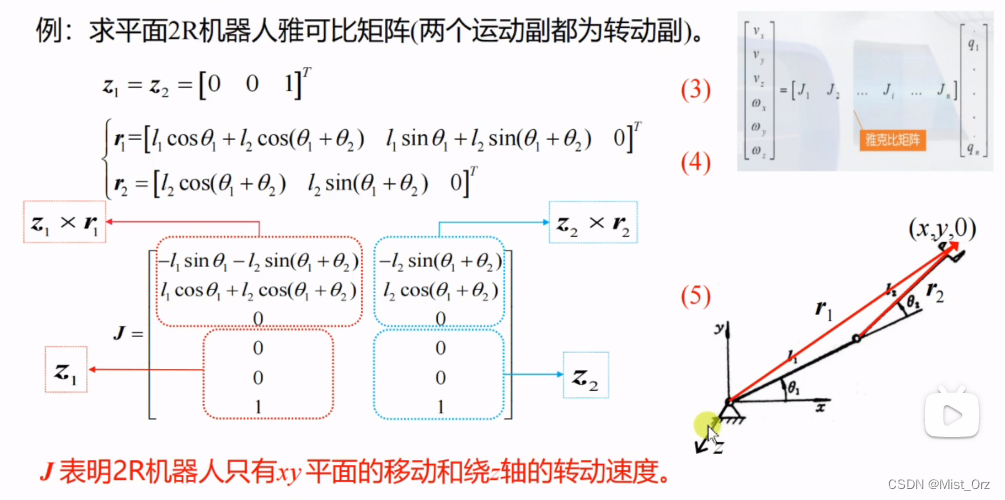
- 矢量积法求scara机器人的雅可比矩阵


○ 微分变换法
· 坐标系的微分运动
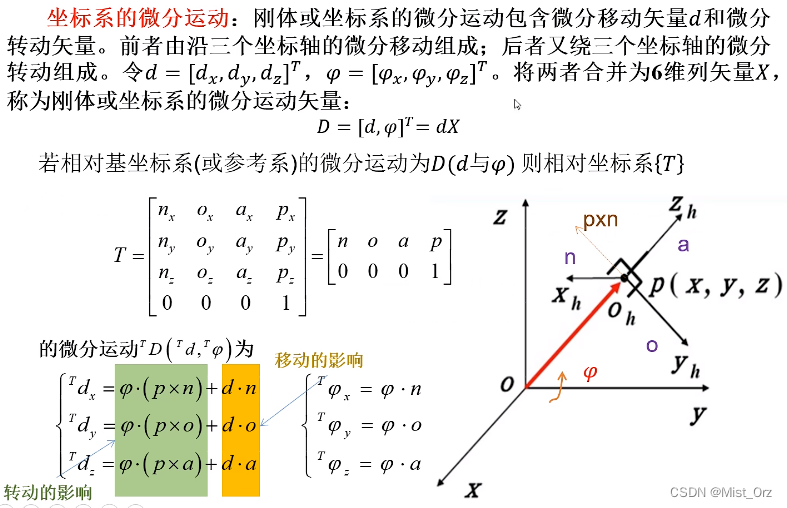
我的理解:
听的不是很明白,感觉视频里的坐标系画的有问题,越看越糊涂,但是大概意思是
- 首先,坐标系的微分运动指的是一个坐标系相对于自己的参考坐标系做的运动的微分,包括微分移动和微分转动
- 然后,运动包括旋转运动和平移运动
- 其次,微分转动仅受旋转运动影响,其值为角速度与变换矩阵的n o a向量的点乘
(【??】关于为什么noa对应xyz方向,我不是很理解,以后弄明白了我再来补充,现在就当是定义了吧。。。)- 再次,微分平移同时收到旋转运动和平移运动的影响,其值为对应方向旋转运动的线速度(也就是叉乘)加上对应方向平移运动的分量(也就是平移速度与n o a的点乘)
· 机器人的微分运动
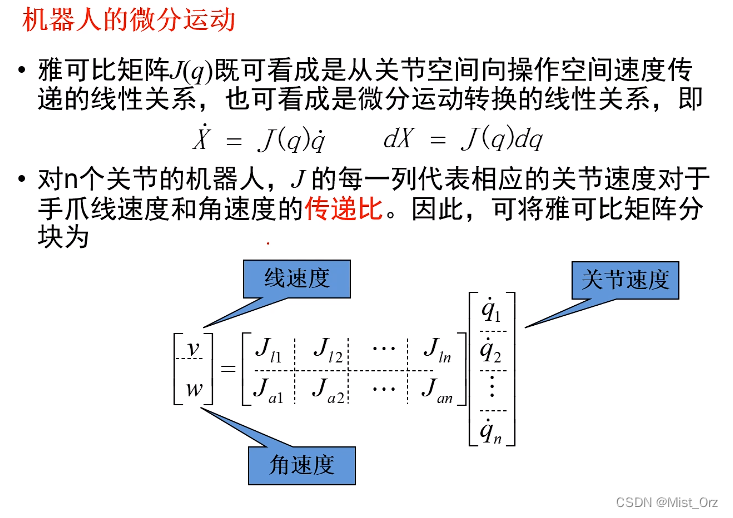
我的理解:
- 这个不用我再理解了,就是机器人的关节速度通过雅可比矩阵转换成末端的线速度与加速度的形式
- 雅可比矩阵每一列都表示对应的关节对机器人末端线速度和角速度的影响
· 微分变换法概念

我的理解:
- 关于为什么这里雅可比矩阵可以写成这样,视频里up说这个就是前面这个公式的矩阵形式
- 但是我觉得他说的 【不对】,如果说这个是6关节机器人的雅可比矩阵,那么后面就没有必要再继续求了,直接就能根据变换矩阵写出对应的雅可比矩阵。而且雅可比矩阵每一列都是对应关节的映射关系,这个矩阵显然不符合。
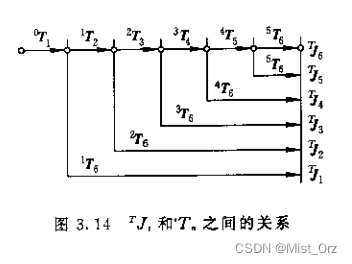
- 结合接下来的讲解(也就是下面这个图),我大概明白了,这个矩阵是对单关节(或者说关节对应的连杆坐标系)相对上一个关节(或者说上一个连杆坐标系)的雅可比矩阵求解方法,后面乘的向量也不是各关节的速度,而是单关节在xyz三个方向的平移和旋转速度分量。
【当然也有可能不是相邻的上一个关节,这要看所带入的其次变换矩阵的】- 因为一个关节往往只对应一个方向的平移或旋转,所以才有如下的结果:


【!注意!】
微分变换法求得的雅可比矩阵,计算后得到的速度向量是相对于末端(工具坐标系)的!
※ 关于相对于末端(工具)坐标系的雅可比矩阵
我想了半天没想明白是什么意思,然后我问了问ChatGPT
ChatGPT yyds!
· 微分变换法求2连杆机械臂雅可比矩阵示例

【?】这DH坐标系建的不对吧?



我的理解:
- 变换矩阵的连乘,目的是构建末端与所求关节的位置关系。
- 只需考虑当前关节和末端的位置关系即可,不需要考虑和前面的坐标系的关系,最后得到的是末端相对当前关节(或者说当前关节所在的连杆坐标系)的速度关系
○ 矢量积法与微分变换法的转换关系
这个问题我找了很多资料都没有提到。
- 首先 矢量积法和微分变换法求得的雅可比矩阵是不相同的
微分变换法自不用说,求解过程很直观,理解起来也容易,他的结果是相对基坐标系(世界坐标系)的映射,也就是我们想要得到的结果
而微分变换法得到的雅可比矩阵是相对于机器人末端坐标系(工具坐标系)的映射,蔡自兴《机器人学》里面有对应的表示
也就是说微分变换法的结果不能直接拿来用,需要将其转换为在基坐标系下的结果。
- 矢量积法与微分变换法的转换关系
我在一个讲雅可比的PPT中看到了他们之间的转换方法

其中 n 0 R T {_n^0}R^T n0RT表示基坐标到末端的齐次变换矩阵的旋转矩阵部分。
【!!!】至于为什么,我也不知道。。。。。希望有大佬来补充
- 另外关于两种方法以及其他方法的对比
这里有一篇文章有更多的讲解,而且文章附上了对应的matlab代码可以参考
→→→【机器人学回炉重造(2-2):雅可比矩阵的求法——矢量积法、微分变换法、Manipulator Jacobian(Jacobian for short)】
△ ZK-500六轴工业机器人的雅可比矩阵
○ 矢量积法
(内容待补充。。。)
○ 微分变换法
(内容待补充。。。)
○ matlab机器人工具箱法
使用机器人工具箱求雅可比,就。。。挺简单的。。。
虽然没有前面的内容,也可以直接用机器人工具箱求雅可比,但是所谓“知其然,又要知其所以然”嘛~
方法可以参考
→→→【matlab机器人工具箱学习笔记——瞬态运动学】
或者我自己的
→→→【Matlab机器人工具箱(Robotics Toolbox)学习笔记】
· jacob0()
- SerialLink.jacob0()
求出对应某个位姿下世界坐标系中的雅克比矩阵
对应矢量积法的结果
· jacobn()
- SerialLink.jacobn()
- 求出对应某个位姿下工具坐标系中的雅克比矩阵
对应微分变换法的结果
· 雅可比矩阵的变换
· matlab代码
- 代码
%ZK-500机器人雅可比矩阵计算——机器人工具箱
clc
clear all;
%% 输入关节角
%这里的输入为角度
theta1=10;
theta2=10;
theta3=10;
theta4=10;
theta5=10;
theta6=10;
%% ZK500机器人MDH参数(m)
% theta(z) d(z) a(x) alpha(x)
%[ 0 d1 0 0 ]
%[ 0+pi/2 0 a1 pi/2 ]
%[ 0 0 a2 0 ]
%[ 0 d4 a3 pi/2 ]
%[ 0 0 0 -pi/2 ]
%[ 0 0 0 pi/2 ]
d1=1.05;
a1=0.5;
a2=1.3;
a3=0.15;
d4=1.2;
dt=0.39;
%将角度转化为弧度
q(1)=theta1/180*pi;
q(2)=theta2/180*pi+pi/2; % 关节2补偿90°
q(3)=theta3/180*pi;
q(4)=theta4/180*pi;
q(5)=theta5/180*pi;
q(6)=theta6/180*pi;
%----------
%机器人工具箱建立机器人模型
% theta(z) d(z) a(x) alpha(x)
L1=Link([ 0 d1 0 0 ],'modified');
L2=Link([ 0 0 a1 pi/2 ],'modified');
L3=Link([ 0 0 a2 0 ],'modified');
L4=Link([ 0 d4 a3 pi/2 ],'modified');
L5=Link([ 0 0 0 -pi/2 ],'modified');
L6=Link([ 0 0 0 pi/2 ],'modified');
Robot_ZK500=SerialLink([L1,L2,L3,L4,L5,L6],'name','ZK-500');
%----------
%输出结果
disp('世界坐标系中的雅可比矩阵:');
J0=Robot_ZK500.jacob0(q)
disp('工具坐标系中的雅可比矩阵:');
Jn=Robot_ZK500.jacobn(q)
- 结果
世界坐标系中的雅可比矩阵:
J0 =
-0.2345 -1.8038 -0.5430 0 0 0
1.3301 -0.3181 -0.0957 0 0 0
0 0.8506 1.0763 0 0 0
0.0000 0.1736 0.1736 0.9254 0.2295 0.8590
0.0000 -0.9848 -0.9848 0.1632 -0.9595 0.1208
1.0000 0.0000 0.0000 0.3420 -0.1632 0.4975
工具坐标系中的雅可比矩阵:
警告: Use jacobe instead of jacobn
> 位置:SerialLink/jacobn (第 981 行)
位置: Jacob_RTB (第 56 行)
Jn =
-0.4584 1.5633 1.1356 0 0 0
-1.2698 -0.5271 -0.4118 0 0 0
-0.0407 -1.1647 0.0575 0 0 0
0.8107 0.3394 0.3394 -0.1710 0.1736 0
-0.3086 0.9402 0.9402 0.0302 0.9848 0
0.4975 0.0302 0.0302 0.9848 0.0000 1.0000
这个“Use jacobe instead of jacobn ”是什么个情况?
大概是新的函数名吧,e可能是end什么的
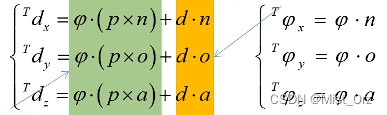






环境搭建](https://img-blog.csdnimg.cn/518050e95c0c4e33a58f9444772c94cf.png)