目录

1.负值和非负值左右划分

2.偶数和奇数的划分

---

数据结构之折半查找（递归和非递归），插值查找和斐波那契查找

归并排序求逆序对（C语言）

1.负值和非负值左右划分

要求：使用尽可能少的时间将一组连续的序列按负值和非负值进行划分，其中负值在左边，非负值在右边（如果存在的零的话，可以放非负值的中任意位置，也可以放在中间）。

提示：由于使用一般的方式来求解这个问题，时间复杂度也不大，比如：首先将为负值的判断出来并输出，已经判断的负值进行标记，那么序列中剩下的就是非负值了，最后直接输出。

但是现在换一种方式来做，也许在这里这种思维没有很好的展现出来，但是在其他场合，这种思维是可以很好的表现出来的。比如下面的序列：

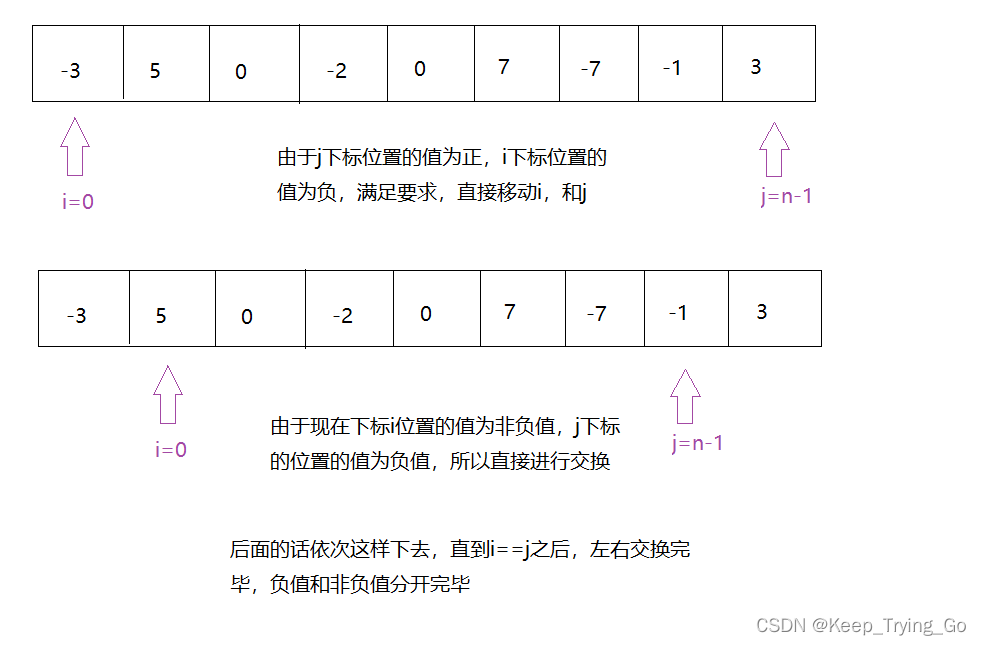
最终结果如下：

初始序列	-3	5	0	-2	0	7	-7	-1	3
最终结果	-3	-1	-7	-2	0	7	0	5	3

 核心算法：

int i=0,j=n-1;
	while(i<j){
        //如果是非负值，j直接向右移动
		while(i<j&&array[j]>=0)j--;
        //如果是负值，i直接向左移动
		while(i<j&&array[i]<0)i++;
        //如果都跳出while循环，那么说明i下标位置的值为非负，j下标位置的值为负值
		if(i<j){
			int temp=array[i];
			array[i]=array[j];
			array[j]=temp;
			j--;
			i++;
		}
	}

提示：但是你会发现上面的最终结果正值和0是穿插一起在左边，那么可以再对左边的非负值再一次使用该算法进行调整，让0值处于整个序列的中间。

调整之后的结果

结果1	-3	-1	-7	-2	0	7	0	5	3
结果2	-3	-1	-7	-2	0	0	7	5	3

完整主程序：

#include<stdio.h>
#include<stdlib.h>
#include<math.h>

#define maxn 20

void exchangeElem(int array[],int n){
	int i=0,j=n-1;
	while(i<j){
		while(i<j&&array[j]>=0)j--;
		while(i<j&&array[i]<0)i++;
		if(i<j){
			int temp=array[i];
			array[i]=array[j];
			array[j]=temp;
			j--;
			i++;
		}
	}
	printf("i=%d  j=%d\n",i,j);
	int k=i+1;
	j=n-1;
	while(k<j){
		while(k<j&&array[j]>0)j--;
		while(k<j&&array[k]==0)k++;
		if(k<j){
			int temp=array[k];
			array[k]=array[j];
			array[j]=temp;
			k++;
			j--;
		}
	}
}

int main(){
	int array[maxn];
	int n;
	printf("请输入元素个数: ");
	scanf("%d",&n);
	printf("请输入元素: ");
	for(int i=0;i<n;i++){
		scanf("%d",&array[i]);
	}
	exchangeElem(array,n);
	for(int i=0;i<n;i++){
		printf("%d  ",array[i]);
	}
	return 0;
}
/*
-3 5 0 -2 0 7 -7 -1 3
-4 5 0 2 -4 3 -9 0 1 -1
1 2 3 4 0 0 0 -1 -2 -3
*/

2.偶数和奇数的划分

要求：将一序列进行奇数和偶数左右划分，奇数放在左边，偶数放在右边。

提示：和上面的负值和非负值的划分是差不读的。

比如划分：1 5 12 34 56 9 5 2 78 45

始序列	1	5	12	34	56	9	5	2	78	45
最终结果	1	5	45	5	9	56	34	2	78	12

核心算法思路：

int i=0,j=n-1;
	while(i<j){
		int temp;
		while(array[i]%2!=0&&i<j){
			i++;
		}
		while(array[j]%2==0&&i<j){
			j--;
		}
		if(i<j){
			temp=array[i];
			array[i]=array[j];
			array[j]=temp;
			i++;
			j--;
		}
	}

完成程序：

#include<stdio.h>
#include<stdlib.h>

#define maxn 100


int array[maxn];
int n;

void exchangElement(){
	int i=0,j=n-1;
	while(i<j){
		int temp;
		while(array[i]%2!=0&&i<j){
			i++;
		}
		while(array[j]%2==0&&i<j){
			j--;
		}
		if(i<j){
			temp=array[i];
			array[i]=array[j];
			array[j]=temp;
			i++;
			j--;
		}
	}
}

int main(){
	printf("请输入元素个数: ");
	scanf("%d",&n);
	printf("请输入元数: ");
	for(int i=0;i<n;i++){
		scanf("%d",&array[i]);
	}
	exchangElement();
	printf("结果: \n");
	for(int i=0;i<n;i++){
		printf("%d  ",array[i]);
	}
	return 0;
}

本人只是觉得这个思维方式来解题还不错，所以才记录。