文心一言 VS 讯飞星火 VS chatgpt （69）-- 算法导论6.5 8题

news2024/9/23 5:33:22

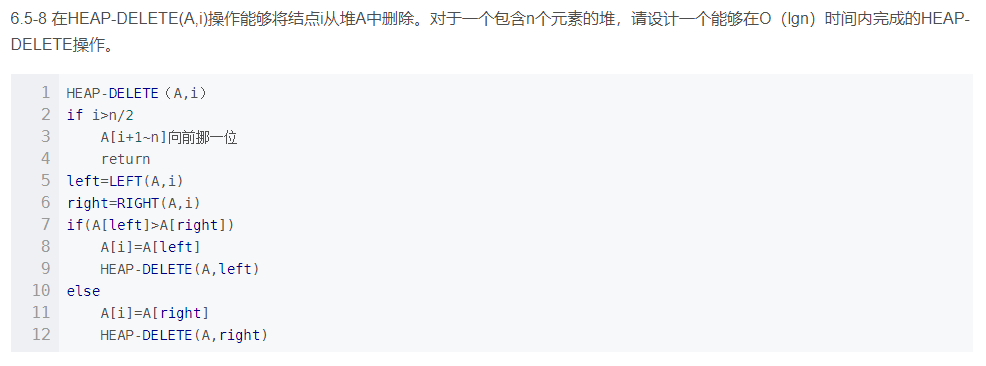
八、HEAP-DELETE(A，i)操作能够将结点 i 从堆 A 中删除。对于一个包含 n个元素的堆，请设计一个能够在 O(lgn)时间内完成的 HEAP-DELETE 操作。

文心一言：

要在 O(log n) 时间内完成 HEAP-DELETE 操作，可以使用以下方法：

1.首先找到要删除的节点 i 的父节点。可以从根节点开始，依次向上遍历，直到找到节点 i。

2.比较节点 i 的值和父节点的值，如果 i 的值比父节点的值大，则将父节点的值与 i 的值交换。

3.然后将 i 的父节点从堆中删除，即执行 HEAP-DELETE(A,父节点)。

4.重复步骤 2 和步骤 3，直到节点 i 的值不再是堆中的最大值。

这个方法的的时间复杂度是 O(log n)，因为每次操作都会将堆的深度减少一半，最多执行 log n 次操作。

以下是这个算法的伪代码：

function heapDelete(A, i)  
    while (i > 1)  
        if (A[i/2] < A[i])  
            break  
        swap(A[i/2], A[i])  
        i = i/2

这里 swap 函数用于交换两个元素的值，heapDelete 函数中用它来交换节点 i 和其父节点的值。

在这里插入图片描述

讯飞星火：

为了在 O(lgn) 时间内完成 HEAP-DELETE 操作，我们可以使用以下策略：

1.从堆的根节点开始，找到要删除的结点 i。

2.如果 i 是根节点，那么直接将左子树的最大结点提升为新的根节点，并删除 i。

3.如果 i 不是根节点，那么比较 i 和其父节点的值。如果 i 的值小于等于其父节点的值，那么将 i 从其父节点的左子树中删除；否则，将 i 从其父节点的右子树中删除。重复这个过程，直到找到要删除的结点 i。

4.在删除结点 i 之后，重新调整堆的结构以保持堆的性质。

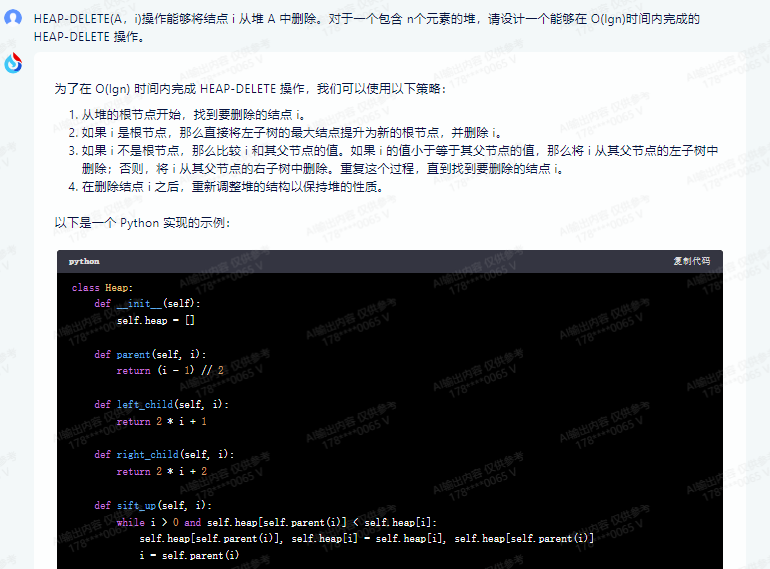
以下是一个 Python 实现的示例：

class Heap:
    def __init__(self):
        self.heap = []

    def parent(self, i):
        return (i - 1) // 2

    def left_child(self, i):
        return 2 * i + 1

    def right_child(self, i):
        return 2 * i + 2

    def sift_up(self, i):
        while i > 0 and self.heap[self.parent(i)] < self.heap[i]:
            self.heap[self.parent(i)], self.heap[i] = self.heap[i], self.heap[self.parent(i)]
            i = self.parent(i)

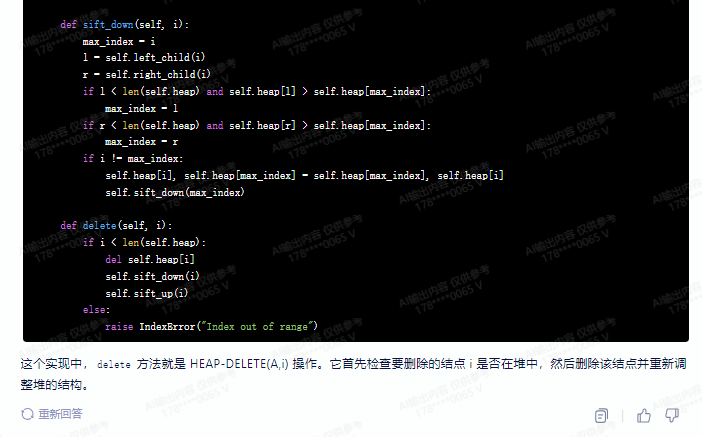
    def sift_down(self, i):
        max_index = i
        l = self.left_child(i)
        r = self.right_child(i)
        if l < len(self.heap) and self.heap[l] > self.heap[max_index]:
            max_index = l
        if r < len(self.heap) and self.heap[r] > self.heap[max_index]:
            max_index = r
        if i != max_index:
            self.heap[i], self.heap[max_index] = self.heap[max_index], self.heap[i]
            self.sift_down(max_index)

    def delete(self, i):
        if i < len(self.heap):
            del self.heap[i]
            self.sift_down(i)
            self.sift_up(i)
        else:
            raise IndexError("Index out of range")

这个实现中，delete 方法就是 HEAP-DELETE(A,i) 操作。它首先检查要删除的结点 i 是否在堆中，然后删除该结点并重新调整堆的结构。

在这里插入图片描述

在这里插入图片描述

360智脑：

这是一个经典的算法问题，可以使用二叉堆的插入和删除操作的时间复杂度为 O(logn),因此可以在 O(logn) 的时间内完成 HEAP-DELETE 操作。具体实现方式可以是在堆顶查找需要删除的元素，然后将其从堆中移除并重新插入堆中即可。

在这里插入图片描述

chatglm：

为了设计一个能够在 O(lgn) 时间内完成的 HEAP-DELETE 操作，我们可以使用二分查找的方法来找到结点 i 在堆中的位置。具体步骤如下：

1.初始化一个指针 p，指向堆 A 中的第一个元素。

2.使用二分查找的方法，找到结点 i 在堆中的位置。具体来说，我们可以先将 p 指向堆的中间位置，然后分别比较 p 左边和右边的元素与 i 的大小关系。如果 p 左边的元素比 i 小，则说明 i 在 p 左边的子树中；否则，如果 p 左边的元素比 i 大，则说明 i 在 p 右边的子树中。我们可以根据这个判断，将 p 指向对应的子树中，并重复上述步骤，直到找到结点 i。

3.将堆顶元素（即 p 指向的元素）与结点 i 交换位置。

4.调整堆，使得交换后的堆仍满足堆的性质。具体来说，我们可以从 p 开始，依次向下调整堆，直到调整到叶子节点为止。

由于使用二分查找的方法，每次查找都可以将查找范围缩小一半，因此，对于一个包含 n 个元素的堆，最多需要进行 logn 次查找。而且，在调整堆的过程中，我们只需要对涉及到的元素进行交换和调整，因此，总的时间复杂度为 O(lgn)。

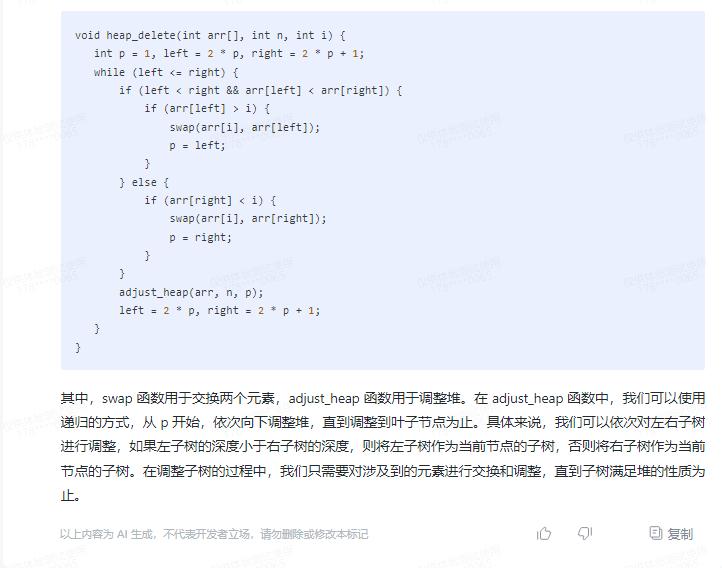
因此，我们可以设计一个能够在 O(lgn) 时间内完成的 HEAP-DELETE 操作，具体实现如下：

void heap_delete(int arr[], int n, int i) {  
   int p = 1, left = 2 * p, right = 2 * p + 1;  
   while (left <= right) {  
       if (left < right && arr[left] < arr[right]) {  
           if (arr[left] > i) {  
               swap(arr[i], arr[left]);  
               p = left;  
           }  
       } else {  
           if (arr[right] < i) {  
               swap(arr[i], arr[right]);  
               p = right;  
           }  
       }  
       adjust_heap(arr, n, p);  
       left = 2 * p, right = 2 * p + 1;  
   }  
}

其中，swap 函数用于交换两个元素，adjust_heap 函数用于调整堆。在 adjust_heap 函数中，我们可以使用递归的方式，从 p 开始，依次向下调整堆，直到调整到叶子节点为止。具体来说，我们可以依次对左右子树进行调整，如果左子树的深度小于右子树的深度，则将左子树作为当前节点的子树，否则将右子树作为当前节点的子树。在调整子树的过程中，我们只需要对涉及到的元素进行交换和调整，直到子树满足堆的性质为止。

在这里插入图片描述

在这里插入图片描述

通义千问：

可以采用双向链表来维护堆结构，同时利用堆的特性保证删除操作的时间复杂度为 O(lgn)。

具体实现如下：

1.定义一个结点类 Node，包含结点的值和指向左右子结点的指针。

2.定义一个双向链表 Head，表示堆的根结点。将 Head 指向的结点标记为堆顶结点。

3.在插入结点时，先将新结点插入到双向链表的末尾，然后进行向下调整，使新结点成为堆顶结点。

4.在删除结点时，先将堆顶结点指向删除结点的右子结点，然后将删除结点的左子结点指向堆顶结点，最后进行向下调整，使堆保持堆的特性。

代码如下：

class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

class Heap:
    def __init__(self):
        self.head = None

    def heapify(self, node, i):
        largest = node
        l = 2 * i + 1
        r = 2 * i + 2

        # 找到左右子结点，并比较大小
        if l < len(self) and self[l].val > largest.val:
            largest = self[l]
        if r < len(self) and self[r].val > largest.val:
            largest = self[r]

        # 如果当前结点大于最大结点，则交换位置，并进行向下调整
        if largest != node:
            self[largest.val, :].left = node
            node.left = self[largest, :]
            self[largest, :].right = node
            node.right = self[largest, :]

            # 如果左子结点存在，则进行向下调整
            if l < len(self) and self[l].val > node.val:
                self.heapify(self[l], l)

            # 如果右子结点存在，则进行向下调整
            if r < len(self) and self[r].val > node.val:
                self.heapify(self[r], r)

    def insert(self, val):
        new_node = Node(val)

        # 如果堆为空，则创建一个新的堆
        if not self.head:
            self.head = new_node
            new_node.left = new_node.right = None
            return

        # 将新结点插入到双向链表的末尾
        new_node.left = self.head
        self.head.right = new_node

        # 进行向下调整，使新结点成为堆顶结点
        self.heapify(new_node, 0)

    def delete(self, val):
        # 定位删除结点的位置
        i = self.search(val)

        # 如果删除结点不存在，则返回空
        if i == -1:
            return

        # 将堆顶结点指向删除结点的右子结点
        self.head.left = self[i].right

        # 将删除结点的左子结点指向堆顶结点
        self[i].left = self.head

        # 进行向下调整，使堆保持堆的特性
        self.heapify(self.head, 0)

    def search(self, val):
        # 遍历整个堆，查找是否存在该结点
        for i in range(len(self) - 1, -1, -1):
            if self[i].val == val:
                return i
        return -1

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

天工：

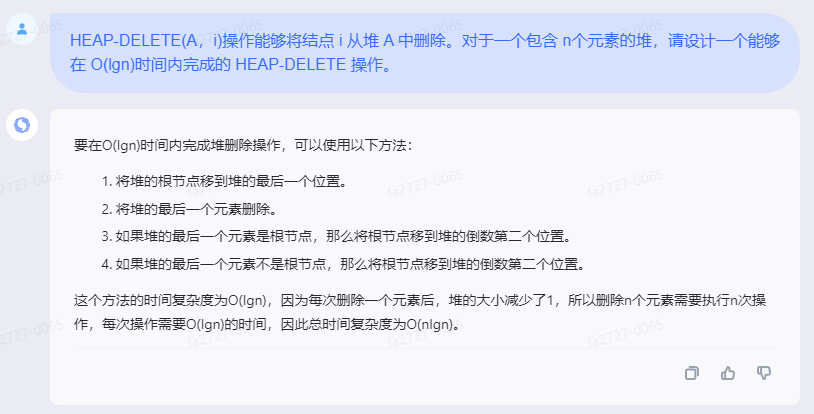
要在O(lgn)时间内完成堆删除操作，可以使用以下方法：

1.将堆的根节点移到堆的最后一个位置。

2.将堆的最后一个元素删除。

3.如果堆的最后一个元素是根节点，那么将根节点移到堆的倒数第二个位置。

4.如果堆的最后一个元素不是根节点，那么将根节点移到堆的倒数第二个位置。

这个方法的时间复杂度为O(lgn)，因为每次删除一个元素后，堆的大小减少了1，所以删除n个元素需要执行n次操作，每次操作需要O(lgn)的时间，因此总时间复杂度为O(nlgn)。

在这里插入图片描述

chatgpt：

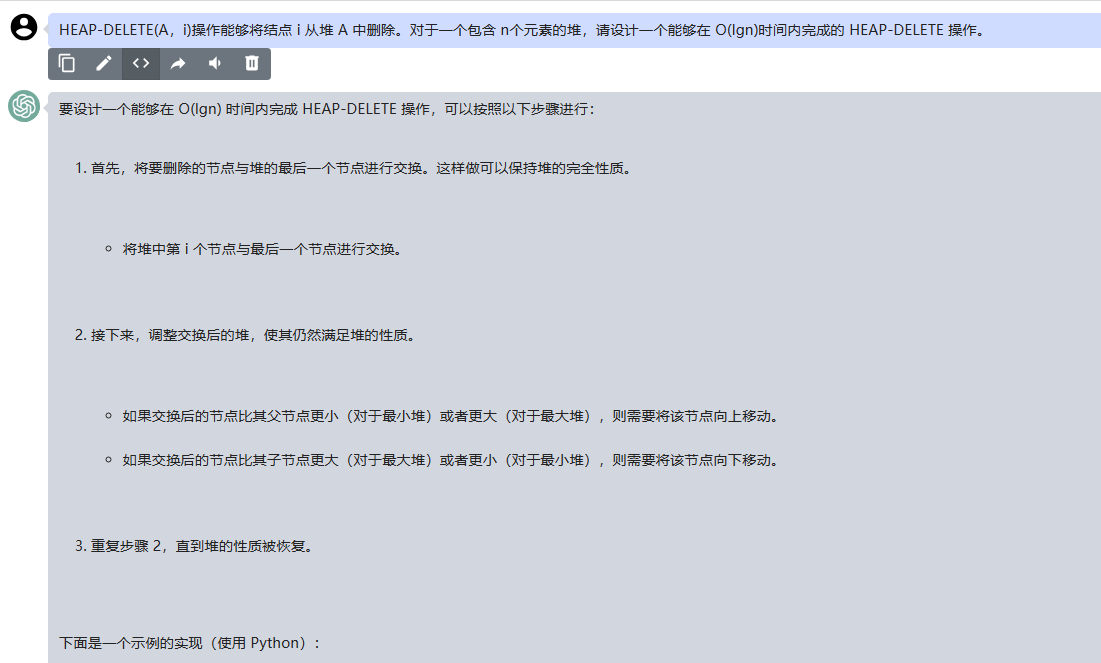
要设计一个能够在 O(lgn) 时间内完成 HEAP-DELETE 操作，可以按照以下步骤进行：

1.首先，将要删除的节点与堆的最后一个节点进行交换。这样做可以保持堆的完全性质。

  • 将堆中第 i 个节点与最后一个节点进行交换。

2.接下来，调整交换后的堆，使其仍然满足堆的性质。

  • 如果交换后的节点比其父节点更小（对于最小堆）或者更大（对于最大堆），则需要将该节点向上移动。

  • 如果交换后的节点比其子节点更大（对于最大堆）或者更小（对于最小堆），则需要将该节点向下移动。

3.重复步骤 2，直到堆的性质被恢复。

下面是一个示例的实现（使用 Python）：

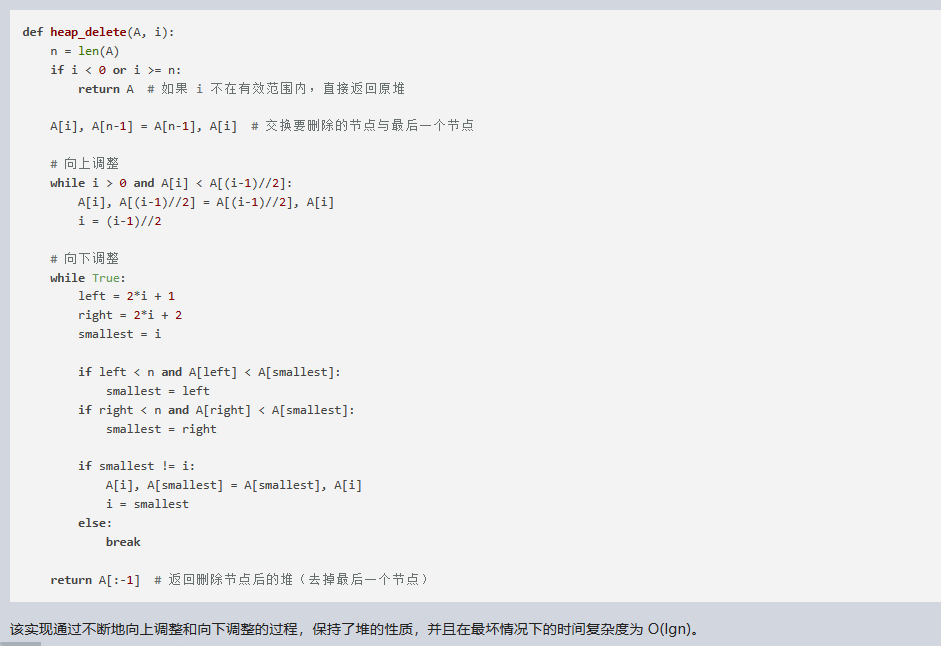
def heap_delete(A, i):
    n = len(A)
    if i < 0 or i >= n:
        return A  # 如果 i 不在有效范围内，直接返回原堆

    A[i], A[n-1] = A[n-1], A[i]  # 交换要删除的节点与最后一个节点

    # 向上调整
    while i > 0 and A[i] < A[(i-1)//2]:
        A[i], A[(i-1)//2] = A[(i-1)//2], A[i]
        i = (i-1)//2

    # 向下调整
    while True:
        left = 2*i + 1
        right = 2*i + 2
        smallest = i

        if left < n and A[left] < A[smallest]:
            smallest = left
        if right < n and A[right] < A[smallest]:
            smallest = right

        if smallest != i:
            A[i], A[smallest] = A[smallest], A[i]
            i = smallest
        else:
            break

    return A[:-1]  # 返回删除节点后的堆（去掉最后一个节点）

该实现通过不断地向上调整和向下调整的过程，保持了堆的性质，并且在最坏情况下的时间复杂度为 O(lgn)。

在这里插入图片描述

在这里插入图片描述

总结

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/823723.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

IPsecVPN实验复现

IPsecVPN实验复现

基础配置&#xff1a; r1&#xff1a; r2&#xff1a; r3&#xff1a; AR1&#xff1a; 一 配置IKE AS 的安全协议&#xff1a; ike proposal 1 ---安全提议编号 encryption-algorithm aes-cbc-128 --- 加密算法 dh group5 ---DH算法 authentication-algorithm md5---…
阅读更多...
一起来学算法（邻接矩阵）

一起来学算法（邻接矩阵）

前言&#xff1a; 邻接矩阵是数学和计算机科学中常用的一种表示方式&#xff0c;用来表述有向图或无向图&#xff0c;一张图由一组顶点&#xff08;或结点&#xff09;和一组表组成&#xff0c;用邻接矩阵就能表示这些顶点间存在的边的关系 1.图的概念 对于图而言&#xff0c;…
阅读更多...
【业务功能篇61】SpringBoot项目流水线 dependencyManagement 标签整改依赖包版本漏洞问题

【业务功能篇61】SpringBoot项目流水线 dependencyManagement 标签整改依赖包版本漏洞问题

业务场景&#xff1a;当前我们项目引入了公司自研的一些公共框架组件&#xff0c;比如SSO单点登录jar包&#xff0c;文件上传服务jar包等公共组件&#xff0c;开发新功能&#xff0c;本地验证好之后&#xff0c;部署流水线&#xff0c;报出一些jar包版本的整改漏洞问题&#xf…
阅读更多...
一文帮你快速理解协程使用模型

一文帮你快速理解协程使用模型

本文同步发表在个人博客上 0xforee’s blog 前言 A coroutine is an instance of suspendable computation. It is conceptually similar to a thread, in the sense that it takes a block of code to run that works concurrently with the rest of the code. However, a co…
阅读更多...
d3dcompiler_47.dll缺失怎么修复，分享几种快速修复方法

d3dcompiler_47.dll缺失怎么修复，分享几种快速修复方法

当我们打开电脑软件或许游戏时候&#xff0c;如果电脑计算机中丢失了d3dcompiler_47.dll就会报错&#xff0c;丢失d3dcompiler_47.dll“”或许找不到d3dcompiler_47.dll等等提示。它主要用于编写和编译Direct3D 11的着色器程序&#xff0c;是Direct3D 11中非常重要的组成部分。…
阅读更多...
FFmpeg下载安装及Windows开发环境设置

FFmpeg下载安装及Windows开发环境设置

1 FFmpeg简介 FFmpeg&#xff1a;FFmpeg是一套可以用来记录、转换数字音频、视频&#xff0c;并能将其转化为流的开源计算机程序。采用LGPL或GPL许可证。它提供了录制、转换以及流化音视频的完整解决方案。项目的名称来自MPEG视频编码标准&#xff0c;前面的"FF"代表…
阅读更多...
Java中集合容器详解：简单使用与案例分析

Java中集合容器详解：简单使用与案例分析

目录 一、概览 1.1 Collection 1. Set 2. List 3. Queue 1.2 Map 二、容器中的设计模式 迭代器模式 适配器模式 三、源码分析 ArrayList 1. 概览 2. 扩容 3. 删除元素 4. 序列化 5. Fail-Fast Vector 1. 同步 2. 扩容 3. 与 ArrayList 的比较 4. 替代方案…
阅读更多...
AutoSAR系列讲解（实践篇）10.8-实验：模式管理

AutoSAR系列讲解（实践篇）10.8-实验：模式管理

首先备份上一次的工程，养成好习惯（最好还是用Git，这次最后再安利一下Git这个神器）。今天的实验异常的简单，基本都是自动配置好了，只需 要勾选上就行，但是大家最好结合前面讲解的内容，把里面的选项点开看看，稍微理解一下。如此，假如配置出错了，才不至于慌乱了手脚 一…
阅读更多...
【C语言】通讯录3.0 （文件存储版）

【C语言】通讯录3.0 （文件存储版）

前言 通讯录是一种记录联系人信息的工具&#xff0c;包括姓名、电话号码、电子邮件地址、住址等。 文章的一二三章均于上一篇相同&#xff0c;可以直接看第四章改造内容。 此通讯录是基于通讯录2.0&#xff08;动态增长版&#xff09;的基础上进行增加文件操作功能&#xff0c…
阅读更多...
jq——页面滚动到显示区域，再执行动画——基础积累

jq——页面滚动到显示区域，再执行动画——基础积累

今天郑大东同事向我显摆了一个他做的动画&#xff0c;效果如下&#xff1a; 使用场景 当页面滚动到相应区域时&#xff0c;再执行里面的动画&#xff0c;也就是下图中右侧的一层层的显示动画&#xff0c;无论是向上滚动页面还是向下滚动页面。 下面直接上代码&#xff1a; …
阅读更多...
mybatis更新时记录变更的字段日志java反射获取字段值转成string

mybatis更新时记录变更的字段日志java反射获取字段值转成string

1.先写个注解,加在entity的字段上,标记要记录这个字段的更新记录&#xff0c;再加个变更记录表&#xff08;你们可以用自己的日志表&#xff09; Retention(RetentionPolicy.RUNTIME) Target({java.lang.annotation.ElementType.FIELD}) Documented public interface ModifyAw…
阅读更多...
iPhone 8透明屏的透明度高吗？

iPhone 8透明屏的透明度高吗？

iPhone 8是苹果公司于2017年推出的一款智能手机&#xff0c;它采用了全新的设计和技术&#xff0c;其中一个亮点就是透明屏。 透明屏是指屏幕具有透明度&#xff0c;可以透过屏幕看到背后的物体。 iPhone 8的透明屏采用了最新的OLED技术&#xff0c;这种技术可以实现更高的对比…
阅读更多...
Jmeter —— jmeter参数化实现

Jmeter —— jmeter参数化实现

jmeter参数化 在实际的测试工作中&#xff0c;我们经常需要对多组不同的输入数据&#xff0c;进行同样的测试操作步骤&#xff0c;以验证我们的软件的功能。这种测试方式在业界称为数据驱动测试&#xff0c; 而在实际测试工作中&#xff0c;测试工具中实现不同数据输入的过程称…
阅读更多...
替代LT8711龙讯替代RTD2172 CS5265中文规格书4K60HZ转接线 设计Type-C转HDMI2.0高清投屏方案

替代LT8711龙讯替代RTD2172 CS5265中文规格书4K60HZ转接线 设计Type-C转HDMI2.0高清投屏方案

龙迅LT8711是一款Type-C/DP1.2 to HDMI2.0方案芯片&#xff0c;北京集睿致远&#xff08;ASL&#xff09;推出的CS5265可以完全代替LT8711UX&#xff0c;封装尺寸比LT8711UX小的同时&#xff0c;CS5265的芯片集成度高&#xff0c;内置MCU&#xff0c;内置lLDO等&#xff0c;CS5…
阅读更多...
【外卖系统】菜品信息分页查询

【外卖系统】菜品信息分页查询

需求分析 当菜品数据很多时&#xff0c;用分页的形式来展示列表数据 代码开发 页面发送ajax请求&#xff0c;将分页查询参数提交到服务端&#xff0c;获取分页数据页面发送请求&#xff0c;请求服务端进行图片下载&#xff0c;用于页面图片展示 构造分页 注意&#xff1a;…
阅读更多...
Unity简单抽奖效果实现

Unity简单抽奖效果实现

实现效果如下&#xff1a; 实现效果为&#xff1a;外部传入数值&#xff0c;正常显示 lhj抽取效果 用户可自定义行为&#xff1a;1&#xff0c;抽取的显示&#xff1b;2&#xff0c;抽取的最低时间 实现代码如下&#xff0c;可自行改写&#xff1a; using System.Collection…
阅读更多...
最新 23 届计算机校招薪资汇总

最新 23 届计算机校招薪资汇总

24 届的秋招提前批已经开始了&#xff0c;比如米哈游、oppoe、tplink 等公司都已经录取开启提前批。 像腾讯、字节、阿里等一线大厂的话&#xff0c;根据往年的情况&#xff0c;估计是 7月下-8 月初。 所以今年参加秋招的同学&#xff0c;要抓紧复习了。 提前批通常就持续不到…
阅读更多...
Minio 部署

Minio 部署

minio 官网&#xff1a;https://www.minio.org.cn/ 部署文档&#xff1a;https://www.minio.org.cn/docs/minio/container/operations/install-deploy-manage/deploy-minio-single-node-single-drive.html# 选择自己的部署环境&#xff1a; 我用的docker: docker pull qua…
阅读更多...
命令模式——请求发送者与接收者解耦

命令模式——请求发送者与接收者解耦

1、简介 1.1、概述 在软件开发中&#xff0c;经常需要向某些对象发送请求&#xff08;调用其中的某个或某些方法&#xff09;&#xff0c;但是并不知道请求的接收者是谁&#xff0c;也不知道被请求的操作是哪个。此时&#xff0c;特别希望能够以一种松耦合的方式来设计软件&a…
阅读更多...
LaTex的下载与安装超详细windows版

LaTex的下载与安装超详细windows版

1.LaTex的下载 &#xff08;texlive下载TexStudio下载&#xff09; &#xff08;1&#xff09;texlive下载&#xff1a; 这里清华镜像下载 &#xff08;2&#xff09;TexStudio下载&#xff1a; 点这里下载镜像 可以根据不同的系统选择不同的版本 2 .LaTex的安装 &#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023