因果推断（二）倾向匹配得分（PSM）

前文介绍了如何通过合成控制法构造相似的对照组，除此之外，也可以根据倾向匹配得分（PSM）进行构造，即为每一个试验组样本在对照组中找对与之相似的样本进行匹配。PSM 通过统计学模型计算每个样本的每个协变量的综合倾向性得分，再按照倾向性得分是否接近进⾏匹配。本文参考自PSM倾向得分匹配法。

⚠️注意：倾向匹配得分常用于截面数据

数据准备

# !pip install psmatching

import psmatching.match as psm
import pytest
import pandas as pd
import numpy as np
from psmatching.utilities import *
import statsmodels.api as sm

以下数据如果有需要的同学可关注公众号HsuHeinrich，回复【因果推断02】自动获取～

# 读取数据
path = "psm_data.csv"
raw_data = pd.read_csv(path)
raw_data.set_index("ID", inplace=True)
raw_data.head()

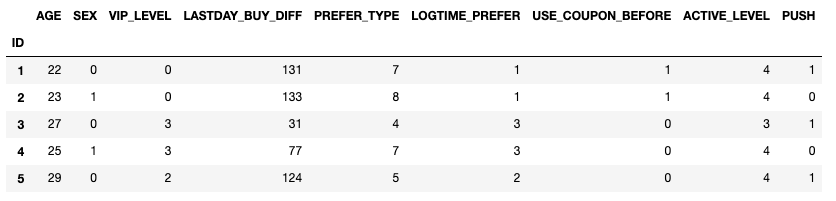
倾向得分与匹配

自定义函数

# 计算propensity
def cal_propensity(df, formula, k):
    df=df.copy()
    # 利用逻辑回归框架计算倾向得分，即广义线性估计 + 二项式Binomial
    glm_binom = sm.formula.glm(formula = formula, data = df, family = sm.families.Binomial())
    # 模型拟合
    result = glm_binom.fit()
    # 计算propensity score
    propensity_scores = result.fittedvalues
    df["PROPENSITY"] = propensity_scores
    
    return df

# 计算matched_data
def cal_matched_data(df, treatment, propensity, k):
    
    groups = df[treatment] # 干预项
    propensity = df[propensity]
    # 把干预项替换成True和False
    groups = groups == groups.unique()[1]
    n = len(groups)
    # 计算True和False的数量
    n1 = groups[groups==1].sum()
    n2 = n-n1
    g1, g2 = propensity[groups==1], propensity[groups==0]
    # 确保n2>n1，,少的匹配多的，否则交换下
    if n1 > n2:
        n1, n2, g1, g2 = n2, n1, g2, g1
        
    # 随机排序干预组，减少原始排序的影响
    np.random.seed(0)
    m_order = list(np.random.permutation(groups[groups==1].index))

    # 根据倾向评分差异将干预组与对照组进行匹配
    # 注意：caliper = None可以替换成自己想要的精度
    matches = {}
    k = int(k)
    print("\n给每个干预组匹配 [" + str(k) + "] 个对照组 ... ", end = " ")
    for m in m_order:
        # 计算所有倾向得分差异,这里用了最粗暴的绝对值
        # 将propensity[groups==1]分别拿出来，每一个都与所有的propensity[groups==0]相减
        dist = abs(g1[m]-g2)
        array = np.array(dist)
        # 如果无放回地匹配，最后会出现要选取3个匹配对象，但是只有一个候选对照组的错误，故进行判断
        if k < len(array):
            # 在array里面选择K个最小的数字，并转换成列表
            k_smallest = np.partition(array, k)[:k].tolist()
            # 用卡尺做判断
            caliper = None
            if caliper:
                caliper = float(caliper)
                # 判断k_smallest是否在定义的卡尺范围
                keep_diffs = [i for i in k_smallest if i <= caliper]
                keep_ids = np.array(dist[dist.isin(keep_diffs)].index)
            else:
                # 如果不用标尺判断，那就直接上k_smallest了
                keep_ids = np.array(dist[dist.isin(k_smallest)].index)
            #  如果keep_ids比要匹配的数量多，那随机选择下，如要少，通过补NA配平数量
            if len(keep_ids) > k:
                matches[m] = list(np.random.choice(keep_ids, k, replace=False))
            elif len(keep_ids) < k:
                while len(matches[m]) <= k:
                    matches[m].append("NA")
            else:
                matches[m] = keep_ids.tolist()
            # 判断 replace 是否放回
            replace = False
            if not replace:
                g2 = g2.drop(matches[m])
                
    # 将匹配完成的结果合并起来
    matches = pd.DataFrame.from_dict(matches, orient="index")
    matches = matches.reset_index()
    column_names = {}
    column_names["index"] = "干预组"
    for i in range(k):
        column_names[i] = str("匹配对照组_" + str(i+1))
    matches = matches.rename(columns = column_names)
    print("\n匹配完成!")
    return matches

# 变量校验
def var_val(df, treatment):
    variables = df.columns.tolist()[0:-2]
    results = {}
    print("开始评估匹配 ...")
    #注意：将PUSH替换成自己的干预项
    for var in variables:
            # 制作用于卡方检验的频率计数交叉表
        crosstable = pd.crosstab(df[treatment],df[var])
        if len(df[var].unique().tolist()) <= 2:
            # 计算 2x2 表的卡方统计量、df 和 p 值
            p_val = calc_chi2_2x2(crosstable)[1]
        else:
            # 计算 2x2 表的卡方统计量、df 和 p 值
            p_val = calc_chi2_2xC(crosstable)[1]
        results[var] = p_val
        print("\t" + var + '(' + str(p_val) + ')', end = "")
        if p_val < 0.05:
            print(": 未通过")
        else:
            print(": 通过")
    if True in [i < 0.05 for i in results.values()]:
        print("\n变量未全部通过匹配")
    else:
        print("\n变量全部通过匹配")

计算得分

# 计算propensity
k=3
formu='PUSH ~ AGE + SEX + VIP_LEVEL + LASTDAY_BUY_DIFF \
        + PREFER_TYPE + LOGTIME_PREFER + USE_COUPON_BEFORE + ACTIVE_LEVEL'
df_model=cal_propensity(raw_data, formu, k)

匹配相似组

# 计算干预=1的匹配组
matches=cal_matched_data(df_model, 'PUSH', 'PROPENSITY', 3)

给每个干预组匹配 [3] 个对照组 ...  
匹配完成!

# 提取全部干预与倾向匹配数据
# 这里直接调用get_matched_data，注意输入的matches是匹配结果，raw_data是全部数据
matched_data = get_matched_data(matches, raw_data)

变量校验

# 变量校验
var_val(df_model, 'PUSH')

开始评估匹配 ...
	AGE(0.9904): 通过
	SEX(0.6688): 通过
	VIP_LEVEL(0.0089): 未通过
	LASTDAY_BUY_DIFF(0.5134): 通过
	PREFER_TYPE(0.7107): 通过
	LOGTIME_PREFER(0.2442): 通过
	USE_COUPON_BEFORE(0.2961): 通过
	ACTIVE_LEVEL(0.7934): 通过

变量未全部通过匹配