文章目录
- 第十三章 利用PCA简化数据
- 13.1降维技术
- 13.2PCA
- 13.2.1移动坐标轴
- 13.2.2在NumPy中实现PCA
- 13.3利用PCA对半导体制造数据降维
第十三章 利用PCA简化数据
PCA(Principal Component Analysis,主成分分析)是一种常用的降维技术,用于将高维数据集转换为低维的表示,同时保留尽可能多的数据信息。它的主要原理是通过线性变换将原始数据投影到一个新的坐标系中,使得数据在新坐标系下的方差最大化。这样,数据的主要特征就能够通过少数几个主成分来表示,从而达到降维的效果。
13.1降维技术
对数据进⾏简化还有如下⼀系列的原因:
- 使得数据集更易使⽤;
- 降低很多算法的计算开销;
- 去除噪声;
- 使得结果易懂
常见的降维技术:
- 主成分分析(PCA):在PCA中,数据从原来的坐标系转换到了新的坐标系,新坐标系的选择是由数据本身决定的。第⼀个新坐标轴选择的是原始数据中⽅差最⼤的⽅向,第二个新坐标轴的选择和第⼀个坐标轴正交且具有最⼤⽅差的⽅向。该过程⼀直重复,重复次数为原始数据中特征的数⽬。我们会发现,⼤部分⽅差都包含在最前⾯的⼏个新坐标轴中。
- 因⼦分析(Factor Analysis)。在因⼦分析中,我们假设在观察数据的⽣成中有⼀些观察不到的隐变量(latent variable)。假设观察数据是这些隐变量和某些噪声的线性组合。那么隐变量的数据可能⽐观察数据的数⽬少,也就是说通过找到隐变量就可以实现数据的降维。因⼦分析已经应⽤于社会科学、⾦融和其他领域中了。
- 独⽴成分分析(Independent Component Analysis,ICA)。ICA假设数据是从N个数据源⽣成的,这⼀点和因⼦分析有些类似。假设数据为多个数据源的混合观察结果,这些数据源之间在统计上是相互独⽴的,⽽在PCA中只假设数据是不相关的。同因⼦分析⼀样,如果数据源的数⽬少于观察数据的数⽬,则可以实现降维过程。
13.2PCA
主成分分析
- 优点:降低数据的复杂性,识别最重要的多个特征。
- 缺点:不⼀定需要,且可能损失有⽤信息。
适⽤数据类型:数值型数据。
13.2.1移动坐标轴
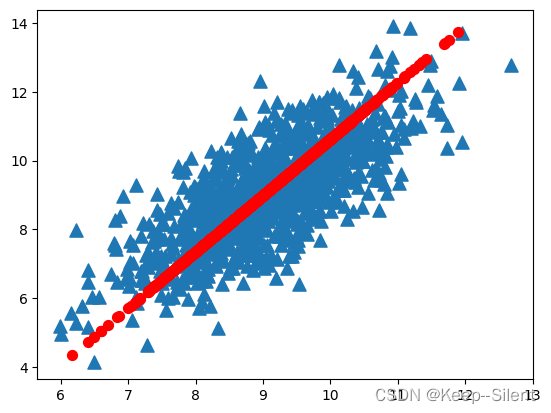
考虑下图,要求画出一条直线,尽可能覆盖这些点。

在PCA中,我们对数据的坐标进⾏了旋转,该旋转的过程取决于数据的本⾝。第⼀条坐标轴旋转到覆盖数据的最⼤⽅差位置,即下图中的红直线
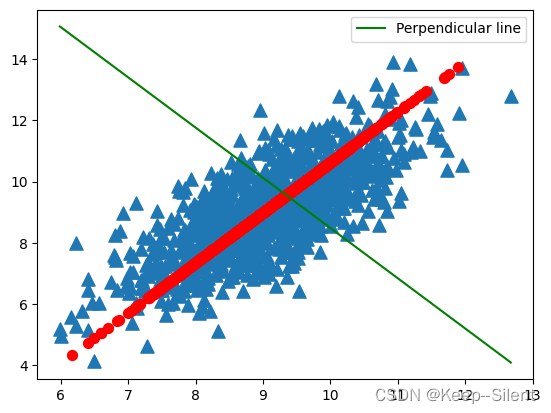
在选择了覆盖数据最⼤差异性的坐标轴之后,我们选择了第二条坐标轴。假如该坐标轴与第⼀条坐标轴正交,它就是覆盖数据次大差异性的坐标轴。如下图
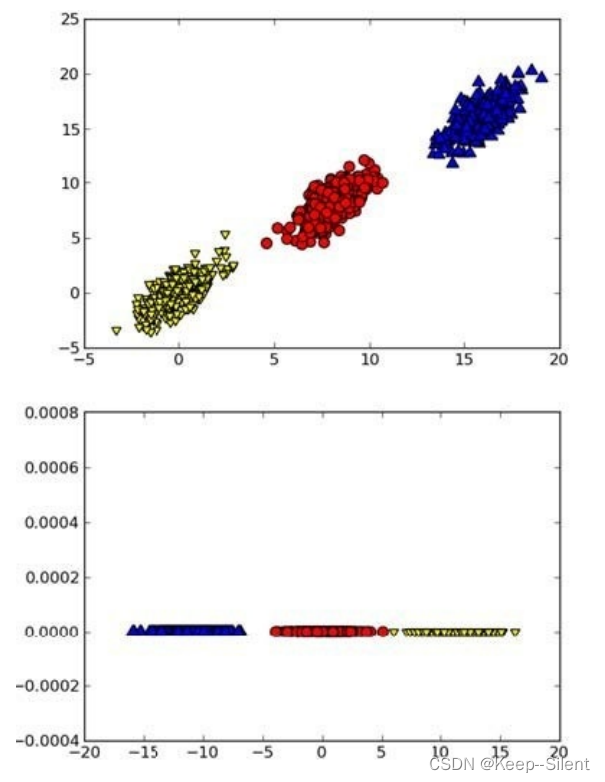
考察下图,其中的数据来⾃于上⾯的图并经PCA转换之后绘制⽽成的。如果仅使⽤原始数据,那么这⾥的间隔会⽐决策树的间隔更⼤。另外,由于只需要考虑⼀维信息,因此数据就可以通过⽐SVM简单得多的很容易采⽤的规则进⾏区分。
13.2.2在NumPy中实现PCA
加载数据集
from numpy import *
import numpy as np
def loadDataSet(fileName, delim='\t'):
fr = open(fileName)
stringArr = [line.strip().split(delim) for line in fr.readlines()]
datArr = [list(map(float, line)) for line in stringArr]
return mat(datArr)
dataMat = loadDataSet('13testSet.txt')
dataMat
matrix([[10.235186, 11.321997],
[10.122339, 11.810993],
[ 9.190236, 8.904943],
...,
[ 9.854922, 9.201393],
[ 9.11458 , 9.134215],
[10.334899, 8.543604]])
PCA过程:
- 去除平均值
- 计算协方差矩阵
- 计算协方差矩阵的特征值和特征向量
- 将特征值从大到小排序
- 保留最上⾯的N个特征向量
- 将数据转换到上述N个特征向量构建的新空间中
def pca(datMat, topNfeat=9999999):
meanVals = datMat.mean(0)
meanRemoved = datMat - meanVals # 1. 去除平均值
covMat = cov(meanRemoved, rowvar=0) # 2. 计算协⽅差矩阵
eigVals, eigVects = linalg.eig(mat(covMat)) # 3. 计算协⽅差矩阵的特征值和特征向量
eigValInd = argsort(eigVals) # 4. 将特征值从⼤到⼩排序
eigValInd = eigValInd[:-(topNfeat+1):-1] # 保留topNfeat个维度
redEigVects = eigVects[:, eigValInd] # 5. 保留最上⾯的N个特征向量
lowDDataMat = meanRemoved * redEigVects # 6. 将数据转换到上述N个特征向量构建的新空间中
reconMat = (lowDDataMat * redEigVects.T) + meanVals
return lowDDataMat, reconMat
显示部分PCA数据
lowDMat, reconMat = pca(dataMat, 1)
print('lowDMat',lowDMat[:3,:])
print('reconMat',reconMat[:3,:])
lowDMat [[-2.51033597]
[-2.86915379]
[ 0.09741085]]
reconMat [[10.37044569 11.23955536]
[10.55719313 11.54594665]
[ 9.01323877 9.01282393]]
进行数据可视化:
- 展示原始所有数据dataMat
- 绘制第一坐标轴reconMat
import matplotlib
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat[:, 0].flatten().A[0], dataMat[:, 1].flatten().A[0], marker='^', s=90)
ax.scatter(reconMat[:, 0].flatten().A[0], reconMat[:, 1].flatten().A[0], marker='o', s=50, c='red')
plt.show()

13.3利用PCA对半导体制造数据降维
dataMat = loadDataSet('13secom.data',' ')
print(shape(dataMat))
print(dataMat[20:24,:4])
(1567, 590)
[[2987.32 2528.81 nan nan]
[ nan 2481.85 2207.3889 962.5317]
[3002.27 2497.45 2207.3889 962.5317]
[2884.74 2514.54 2160.3667 899.9488]]
可以看出数据量1567,和数据维度590
其中,数据中有NaN数据需要处理,接下来处理NaN数据
def replaceNanWithMean(dataMat):
numFeat = shape(dataMat)[1]
for i in range(numFeat):
meanVal = mean(dataMat[nonzero(~isnan(dataMat[:,i].A))[0],i]) #values that are not NaN (a number)
dataMat[nonzero(isnan(dataMat[:,i].A))[0],i] = meanVal #set NaN values to mean
return dataMat
dataMat=replaceNanWithMean(dataMat)
print(dataMat[20:24,:4])
[[2987.32 2528.81 2200.54731771 1396.37662737]
[3014.45289558 2481.85 2207.3889 962.5317 ]
[3002.27 2497.45 2207.3889 962.5317 ]
[2884.74 2514.54 2160.3667 899.9488 ]]
可以看到NaN已经处理为了平均值
计算特征值
meanVals = dataMat.mean(0)
meanRemoved = dataMat - meanVals # 1. 去除平均值
covMat = cov(meanRemoved, rowvar=0) # 2. 计算协⽅差矩阵
eigVals, eigVects = linalg.eig(mat(covMat)) # 3. 计算协⽅差矩阵的特征值和特征向量
eigVals = sort(eigVals) # 4. 将特征值从⼤到⼩排序
print(eigVals)
[-1.77898285e-16 -6.91541208e-19 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
0.00000000e+00 0.00000000e+00 6.06554565e-18 9.84684997e-16
4.76825507e-15 1.80003664e-10 1.97062976e-10 2.61901629e-10
5.27591520e-10 6.13351286e-10 6.95078509e-10 9.24977925e-10
...
1.25591691e+03 1.33096008e+03 1.53948465e+03 1.66199683e+03
1.70492093e+03 1.76741826e+03 1.86414157e+03 2.16835314e+03
2.35027999e+03 2.74523635e+03 3.24193522e+03 3.41199406e+03
4.10673182e+03 4.23060022e+03 4.95614671e+03 5.34196392e+03
7.22765535e+03 8.34665462e+03 9.48876548e+03 1.04841308e+04
1.09321187e+04 1.44089194e+04 1.47123429e+04 2.67385181e+04
3.31436743e+04 3.55294040e+04 4.15532551e+04 4.41914029e+04
4.54661746e+04 5.03324580e+04 5.16269933e+04 5.96776503e+04
6.52620058e+04 6.66060410e+04 7.76560524e+04 8.15850591e+04
8.33473762e+04 1.00166164e+05 1.02849533e+05 1.08493848e+05
1.13215032e+05 1.52422354e+05 1.86856549e+05 1.96098849e+05
2.08513836e+05 2.37155830e+05 2.83668601e+05 2.90863555e+05
4.67693557e+05 1.31540439e+06 2.07388086e+06 8.24837662e+06
2.17466719e+07 5.34151979e+07]
其中有大量特征值都是0。这就意味着这些特征都是其他特征的副本,也就是说,它们可以通过其他特征来表示,而本身并没有提供额外的信息
我们可以尝试不同的截断值来检验它们的性能。有些人使用能包含90%信息量的主成分数量,而其他人使用前20个主成分。我们无法精确知道所需要的主成分数目,必须通过在实验中取不同的值来确定。有效的主成分数目则取决于数据集和具体应用。
上述分析能够得到所用到的主成分数目,然后我们可以将该数目输入到PCA算法中(如lowDMat, reconMat = pca(dataMat,20)),最后得到约简后数据就可以在分类器中使用了。
![Error in v-on handler (Promise/async): “[object Object]“](https://img-blog.csdnimg.cn/821f7c1a4d0843b88115e484cee87998.png)