导论

首先来思考一个十进制小数是如何被转化成二进制的。它使用的方式：乘基取整。你想把它化成n进制，基数就是n。以小数0.6875为例，将它化成二进制

那么它化成二进制0.1101。以原码或补码表示成01101。
并不是每一个十进制小数都可以化成2进制，根据小数转化成二进制的规则来看，如果一个小数 ✖有限个2，能够变成一个整数，那么这个小数就可以用二进制来表示。

例如，0.3不管它✖多少个2，都没有办法变成整数，这个“乘基取整”的过程就没有出口，所以0.3不能用二进制表示。

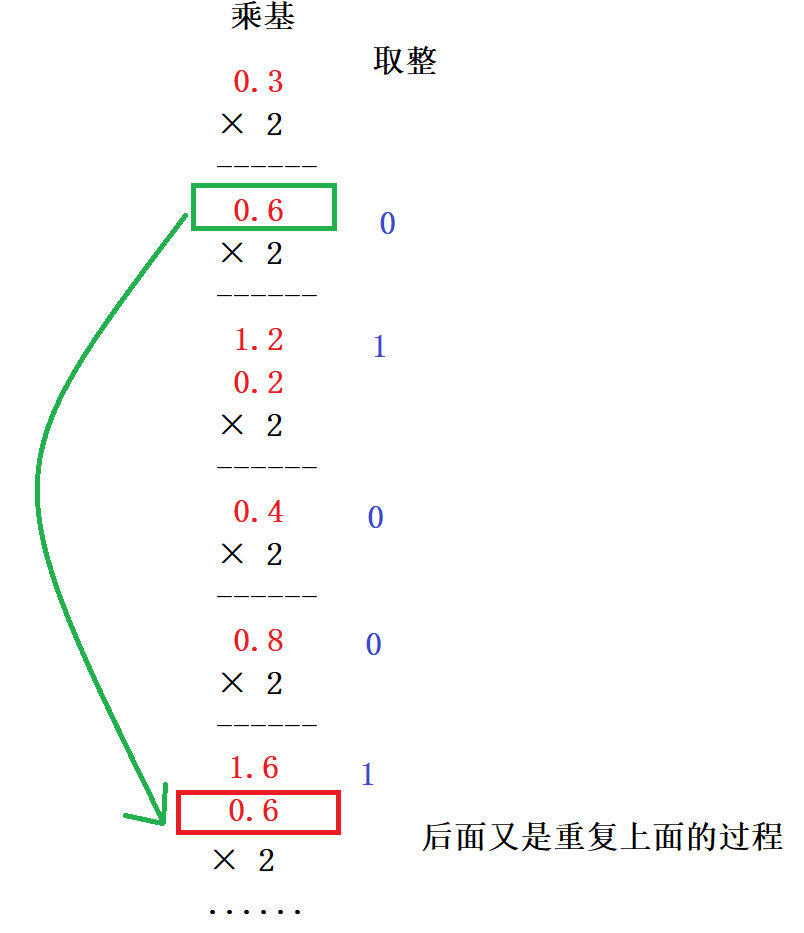
另外，根据“乘基取整”的规则来看，小数乘了多少个2，那么它就用多少个二进制表示。

推理过程

根据上面导论里得出来的两个结论，进行推导。

• 如果一个小数 ✖有限个2，能够变成一个整数，那么这个小数就可以用二进制来表示
• 小数乘了多少个2 变成了整数，那么它就用多少个二进制表示。

以数学角度来说，一个小数m∈（0, 1)，乘以n个2，可以变成整数N，那么这个小数就可以用n位的二进制表示出来。根据题意可以列出表达式

$$m\times 2^n=N$$
$$小数\times 2^n=整数$$
即上述这个等式如果成立，小数m就可以用n位的二进制表示，那么就有如下过程：
$$0\le m=\frac{N}{2^n}<1$$
$$0\le 小数=\frac{整数}{2^n}<1$$
因为m是小数，我们可以列出上述不等式。
$$0\le N<2^n$$
$$0\le 整数<2^n$$
N仅仅规定是整数，N可以是0、1、2、… 、2^n-1 ，即m有2ⁿ个可能值。
所以n位的二进制可以表示2ⁿ个小数

---

1位二进制，可以表示多少个小数:
$$0\le m=\frac{N}{2^1}<1$$
即
$$0\le N<2^1$$

且N是整数，N可以是0、1。
1位二进制可以表示 2⁰ 个小数

---

2位二进制，可以表示多少个小数:
$$0<m=\frac{N}{2^2}<1$$
即
$$0<N<4$$
且N是整数，N可以是0、1、2、3。
2位二进制可以表示 2² 个小数

---

3位二进制，可以表示多少个小数:
$$0<m=\frac{N}{2^3}<1$$
即
$$0<N<2^3$$
且N是整数，N可以是0、1、2、……、2³-1。
3位二进制可以表示 2³ 个小数

---

结论

综上，不考虑符号位，n位的二进制可以表示2ⁿ个小数。

练习

对于相同位数（设为N位，不考虑符号位）的二进制补码小数和十进制小数，二进制小数能表示数的个数/十进制小数所能表示数的个数为________.

解答：
不考虑符号位，N位的二进制可以表示2^N个小数。
而不考虑符号，N位的十进制小数，能够表示10^N个小数。例如，3位小数部分，最大可以表示0.999，那么可以表示的范围是 0~0.999，一共可以表示10^N个小数。
所以$$\frac{二进制小数所能表示数的个数}{十进制小数所能表示数的个数}=\frac{2^N}{10^N}=(0.2{)}^N$$