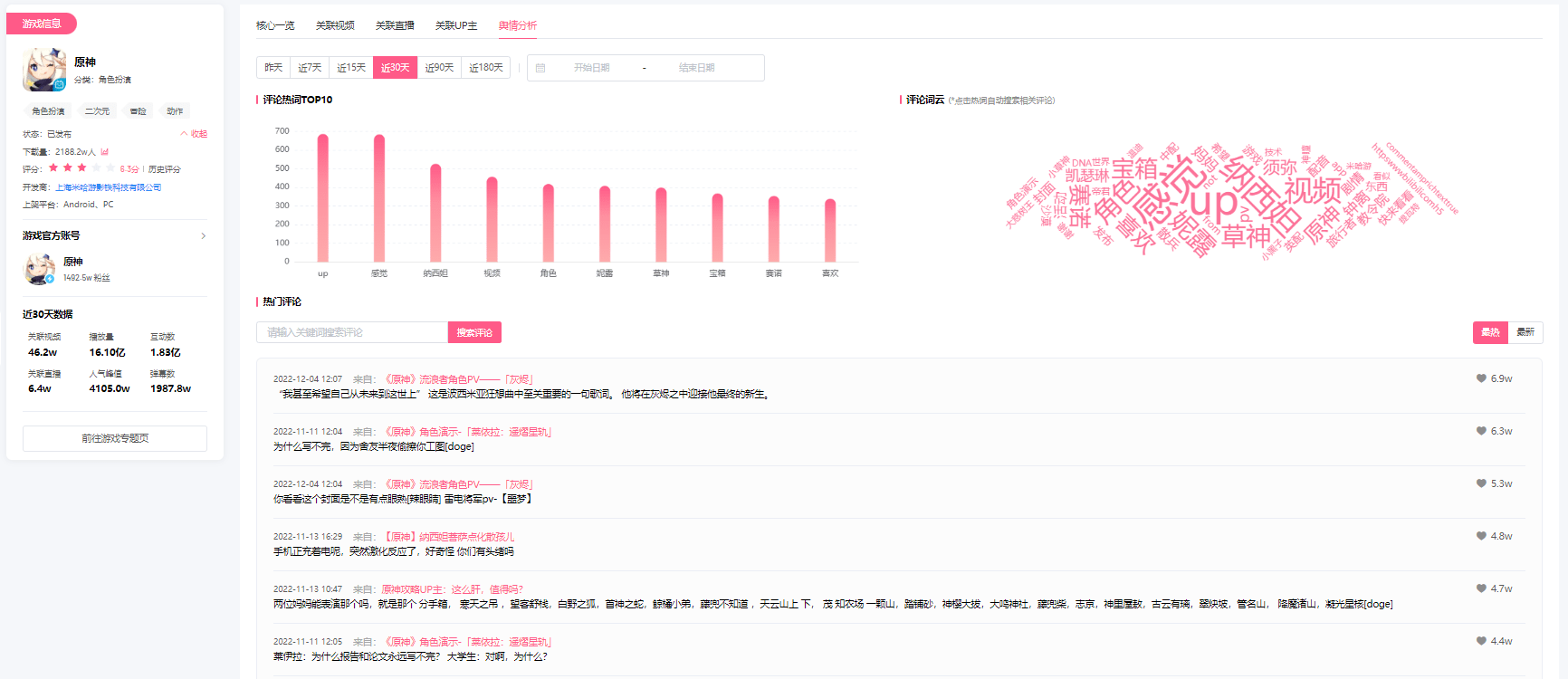
持续集成是一种软件开发实践，即团队开发成员经常集成他们的工作，通常每个成员每天至少集成一次，也就意味着每天可能会发生多次集成。每次集成都通过自动化的构建（包括编译，发布，自动化测试)来验证，从而尽快地发现集成错误。许多团队发现这个过程可以大大减少集成的问题，让团队能够更快的开发内聚的软件。

在上一篇《【AI工程论文解读】04-通过Ease.ML/CI实现机器学习模型的持续集成（上）》文中，我们介绍了ease.ml/ci的系统设计和基本实现，本篇将主要分享基于ease.ml/ci进行的优化和实验。

优化

如前所述，ease.ml/ci基本实现无法为低容错和或自适应场景提供可用的方案。因此，需要对进一步优化样本量估计器。

High-level Intuition

本节中我们提出的所有技术都基于相同的洞察：在最坏的情况下，收紧样本估计量很难比O(1/ϵ2)更好；相反，我们采取经典的系统思维方式—对普遍的测试条件进行样本估计量的改进。因此，对于不同形式的测试条件，ease.ml/ci采用不同的优化技术。

技术观察1

 技术观察2

如果要估计新模型和旧模型之间的预测差异，不需要有标记。相反，来自未标记数据集的样本就足以估计差异。此外，当只有10%的数据点具有不同的预测时，为了估计n−o，只需为整个测试集中的10%提供标记。

模式1：基于差异的优化（Difference-based Optimization）

ease.ml/ci在公式中搜索的第一个模式是它是否符合以下形式

d < A + / − B /\ n − o > C + / − D

上述限制了新模型允许的变更量，并同时确保新模型不比旧模型差。这两个子句经常出现在用户的测试条件中：对于生产级系统，开发人员从部署模型开始，并花费大部分时间微调机器学习模型。因此，持续集成测试必须具有低至单个精度点的容错。另一方面，新模型与旧模型不会有明显的区别，否则会花费需要更多的调试和研究。

假设一种优化方案，获取无标记的数据样本相对便宜，而提供标记则比较昂贵。当此假设有效时，分层测试和主动标记中两种优化都可以应用于此模式；否则，两种优化仍然适用，但只会对一个子集进行改进。

分层测试（Hierarchical Testing）

主动标记（Active Labeling）

前面的示例为用户提供了一种只用67K样本执行32个完全自适应微调步骤的方法。假设开发人员每天执行一次提交，这意味着我们每个月需要67K个示例来支持持续集成服务。

该策略的一个潜在挑战是，在持续集成服务开始工作之前，需要对所有67K个样例进行标记。在理想的情况下，我们希望将开发工作与标记工作交织在一起，并随着时间的推移对标记工作进行分摊。

主动标记假定是一个平稳的底层分布。在系统中实现该目的的方法是要求用户同时提供一个未标记的数据点池，然后仅在需要时要求提供标记。这样，就不需要随着时间的推移绘制新的样本。

模式2：隐式方差边界（Implicit Variance Bound）

在很多情况下，用户没有对新模型和旧模型之间的差异提供明确的约束。然而，许多机器学习模型的预测结果并没有那么大的差异。以AlexNet、ResNet、GoogLeNet、AlexNet（Batch Normalized）和VGG为例：当应用于ImageNet测试集时，这五个开发的模型只会在top-1的正确性上产生至多25%的不同答案，而在前5的正确性上只会产生15%的不同答案。因此，对于持续集成工作，期望多次提交的差异小于经过多年开发的ImageNet的差异并非不合理。

受此启发，ease.ml/ci将自动匹配以下模式：

n−o>C+/−D.

当无标记测试集的获取成本较低时，系统将使用一个测试集来估计 d 高达 ϵ=2D ：对于二项分类任务，系统可以使用无标记测试集；对于多类任务，既可以在未标记的测试集上测试预测的差异，也可以在标记的测试集上测试正确性的差异。这给了一个 n−o 的上限。然后，系统在另一个测试集(与测试d所用的测试集不同)上测试 n–o 直到 ϵ=D 。当这个上限足够小时，系统将触发类似于模式1中的优化。

需要注意的是在执行该方法之前，系统不知道第二个测试集的大小。如果需要，系统会使用一种类似于主动标记的技术，即在每次提交新模型时通过递增的方式增加标记的测试集。具体来说，根据模式优化测试条件

n>A+/−B,

当 A 较大（如0.9或0.95）时，可以先对n的下限进行粗略预估，然后根据该下限来实现。这种改进方法只能在下限较大（例如0.9）时引入。

严格的数值边界（Tight Numerical Bounds）

在（Langford,2005）之后，可以从Bernoulli分布中提取的 n i.i.d随机变量组成的测试条件，人们可以简单地导出达到 (ϵ,δ) 精度所需的样本数。样本数的计算需要使用Binomial distribution (sum of i.i.d Bernoulli variables)。Tight Bound是通过取所需样本数 n 的最小值，而不是未知的最大真平均值 p 来解决的。这种技术也可以扩展到更复杂的查询，其中二项分布必须被多模态分布取代。对于简单的情况，精确的分析没有封闭的解，推导有效的近似值留待后续工作。

图3 基本实现和优化实现中样本量估计器的比较

实验

样本量估计器

通过样本方差的上限，相对于Hoeffding边界，能够使用更严格的边界。上限可以通过使用未标记的数据点来估计新模型和旧模型之间的差异来获取；也可以在使用标记的数据点前先进行粗略估计获取。本文中，验证了我们的理论界限及其对提高标记复杂性的影响。

图3中，通过假设不同的上限 p ，对于精度在98%左右的模型，给出了估计误差和经验误差。通过在无限MNIST数据集（Bottou,2016）上运行GoogLeNet（贾等人，2014），并估计真实精度 c 。假设在非自适应场景，通过随机抽取 n 个数据点获得了一系列精度。然后，用给定的样本数n和概率 1−δ 估计区间 ϵ 。可以得出，基本实现和ease.ml/ci都具有经验误差，正如预期的那样，ease.ml/ci使用的样本数量明显较少。

图4中展示了上限对提高标记复杂性的影响。可以看到，当 p 相当小时，改进显著增加；当 p=0.1 时，在标记复杂性上几乎实现10倍的改进。而主动标记更进一步进行了改善，正如预期的那样，又增加了10倍。

图4 _、_和p对标记复杂度的影响

进行中的ease.ml/ci

作者根据SemEval-2019任务3竞赛的机器学习模型开发了基于ease.ml/ci的三种不同测试条件，在开发测试条件时采用了非自适应场景。图5展示了三个相似但不同的测试条件，在非自适应场景下，前两个条件检查新模型是否比旧模型至少好2个百分点。第三个条件模拟了用户在每次提交后都会得到反馈，没有任何false negative。ease.ml/ci使用模式2优化了所有三个查询，任意两个提交之间的预测差异不超过10%。

图5 ease.ml/ci中的持续集成

前两个条件可以在2个百分点的容错范围内和0.998可靠性内解答。第三种情况下的全自适应查询只能实现2.2个百分点的容错性，由于所需的标记数量将超过6K，具有与前两个查询相同的容错性。

可以看到，在所有三种情况下ease.ml/ci返回的是直观意义的通过/失败信息。如果细看在8个迭代中开发和测试精度的演变（见图6），理想的情况是开发人员希望ease.ml/ci接受其最后一个提交，而所有三个查询都将选择倒数第二个模型作为生产模型，主要和测试精度的演变相关。

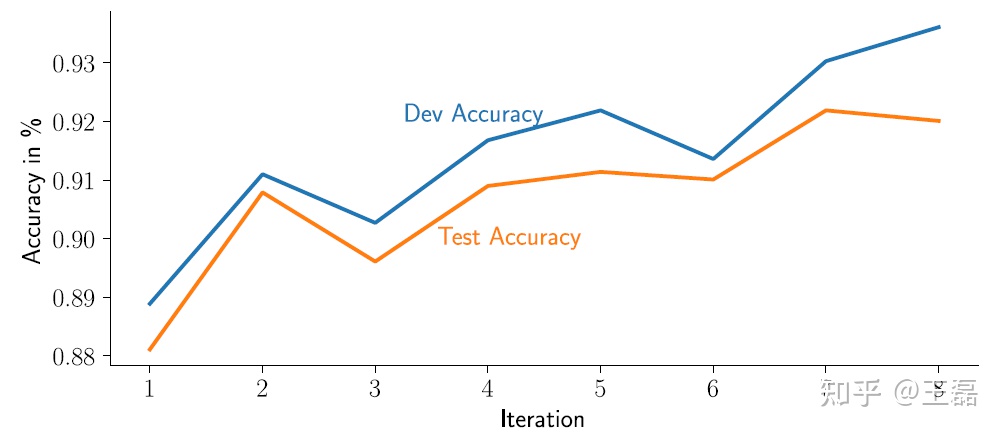
图6 开发和测试精度的演变

结论

ease.ml/ci，一个用于机器学习的持续集成系统，提供了一种声明性脚本语言，允许用户用严格的概率保证来声明丰富的测试条件类。同时，作者们还研究了针对于机器学习模型的标记管理工作的实用性问题。基于作者们的持续集成技术，可以将实际生产系统中使用的测试条件所需的标记数量降低两个数量级。作者们对技术的可靠性已做了验证，并展示了其在实际生产场景中的应用。

附录A 语法和语义

A.1 语法

为了指定条件，每当提交新模型时，将通过ease.ml/ci进行测试，用户使用以下语法：

c   :- floating point constant
v   :- n | o | d
op1 :- + | -
op2 :- *
EXP :- v | v op1 EXP | EXP op2 c
cmp :- > | <
C   :- EXP cmp c +/- c
F   :- C | C /\ F

F作为最终条件，它是一组子句 C 的集合。每个子句都是基于{ n,o,d }的表达式和常数之间的比较，符号 +/− 后面有一个容错。例如，重点优化的两个表达式如下：

n−o>0.02+/−0.01/ d<0.1+/−0.01

其中第一个子句

n−o>0.02+/−0.01

要求新模型的精度比旧模型高两分，容错率为1个点，而子句

d<0.1+/−0.01

要求新模型只能改变旧预测的10%，容错率为1%。

A.2 语义

与传统的连续积分不同，ease.ml/ci、{ n,o,d }中使用的三个变量都是随机变量。因此，对ease.ml/ci条件的评估具有内在的概率性。用户还需要提供2个额外的参数来定义测试条件的语义：（1） δ ，允许测试过程出错的概率，通常选择小于 0.001 或 0.0001 (即 0.999 或 0.9999 成功率)；（2）从{ fp−free,fn−free }中选择模式，它指定测试是无 false−positive 或者无 false−negative 。其语义是，在概率为 1−δ 的情况下，ease.ml/ci的输出不存在 falsepositive 或者 falsenegative 。

falsepositive 或 falsenegativ 的概念与统计假设实验中“I型”错误和“II型”错误之间的基本权衡有关。考虑

参考资料

1. Cedric Renggli, Bojan Karlaš, Bolin Ding, Feng Liu,Wentao Wu, Ce Zhang, Continuous Integration of Machine Learning Models with ease.ml/ci: Towards a Rigorous Yet Practical Treatment SysML Conference (SysML 2019)