线性表基础
线性表概念
线性表就是具有相同特征数据元素的一个有限序列,其中包含元素的个数称为线性表的长度
线性表类型
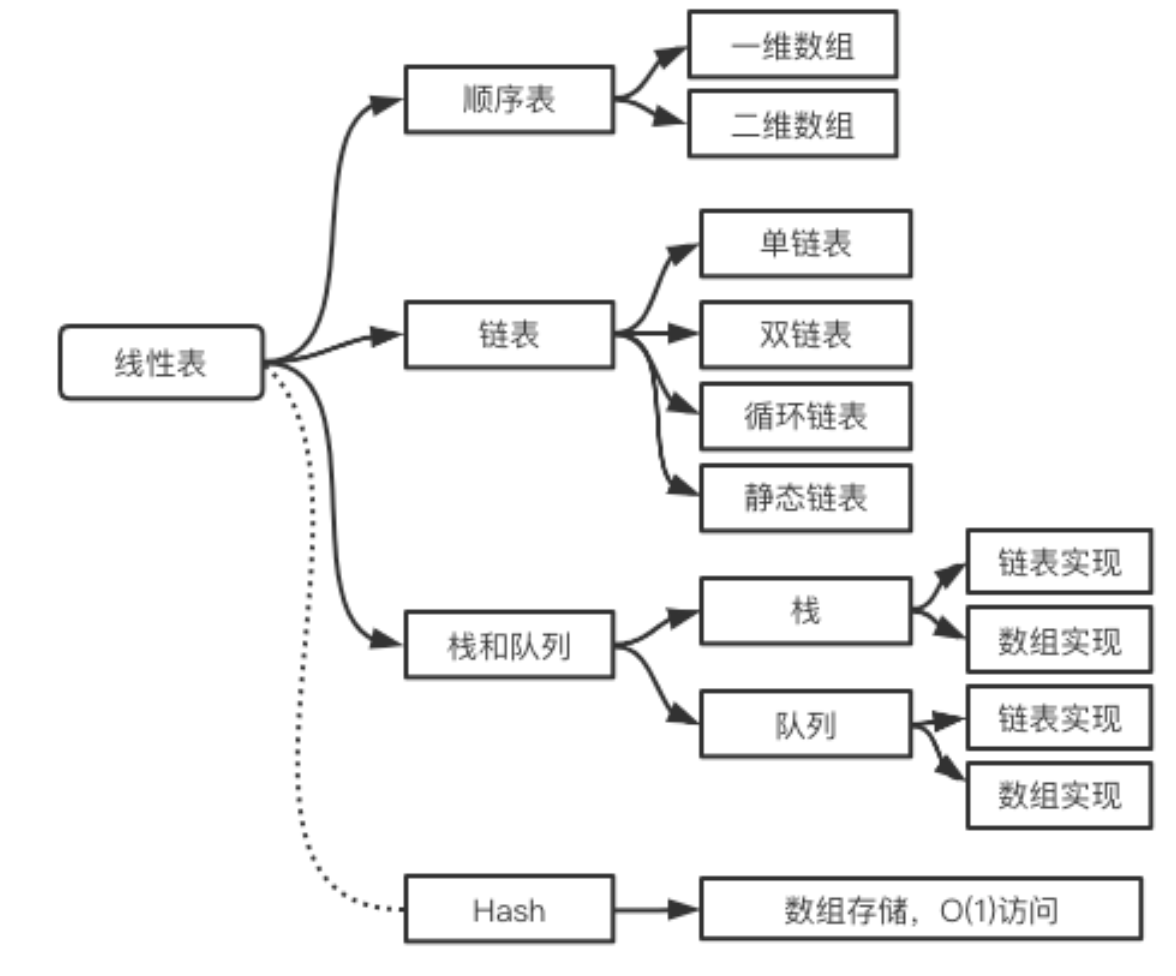
从不同的角度看,线性表有不同的分类
语言实现角度
顺序表有两种实现方式
一体式
分离式
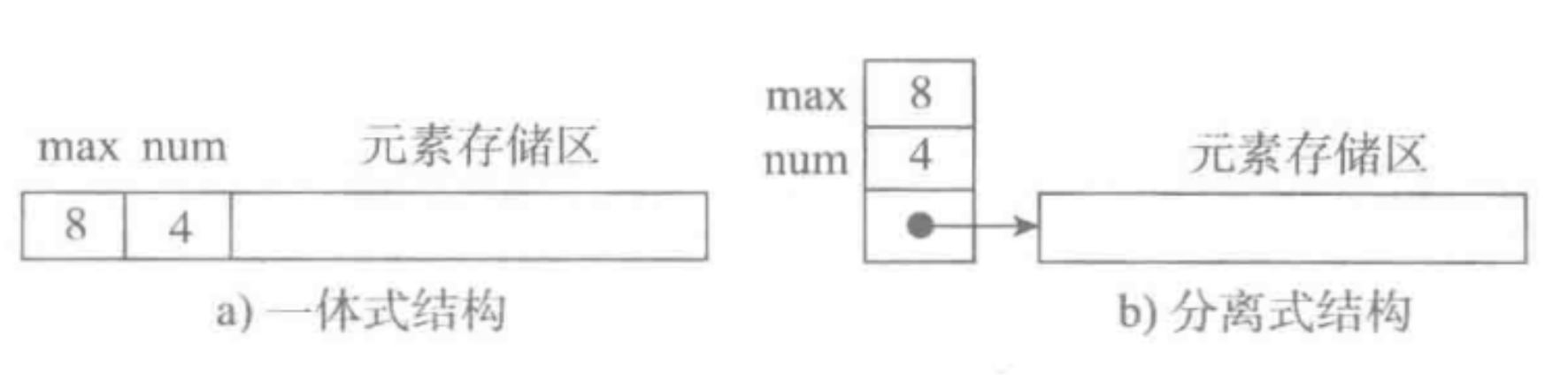
一体式结构
一体式:存储信息的单元 和 元素存储区 以连续的方式被安排在一块存储区里,两部分数据的整体形成一个完整的顺序表对象。
这种结构整体性强,易于管理,但是由于数据元素存储区是表对象的一部分,顺序表创建后,元素存储区就固定了
C和C++都是一体式的结构
分离式结构
分离式:表对象里只保存与整个表有关的信息(容量和元素个数),实际数据元素被放在另一个独立的元素存储区里,通过连接与基本表对象关联
Java和Python是分离式结构
存储角度
顺序型
链表型
顺序型存储
顺序型:就是将数据存放在一段固定的区域内,此时访问元素的效率非常高,但是删除和增加元素代价比较大,如果要扩容,只能整体搬迁。
链表型存储
链表型:元素之间是通过地址一次连接的,因此访问时必须从头开始逐步向后找,查找效率低;而删除和增加元素非常方便,并且也不需要考虑扩容的问题。
链表型的常见实现方式有:单链表、循环链表、双向链表等。
访问限制的角度
受限线性表
栈和队列被称为访问受限的线性表。因为它们的 插入和删除操作受到了限制,只能在固定的位置进行。
Hash比较特殊, 其内部真正存储数据的一般是数组,但是访问是通过映射来实现的,因此大部分材料中并不将Hash归结到线程表中
扩容角度
动态顺序表
采用分离式结构的顺序表,若将数据区更换为存储空间更大的区域,则可在不改变表对象的前提下对其数据存储区进行扩充,所有使用这个表的地方都不必修改,只要程序的运行环境还有空闲存储。
这种表结构不会因满了二导致操作无法进行,人们把采用这种技术实现的顺序表称为动态顺序表,因为其容量可以在使用中动态变化。
扩充的策略
- 每次扩充增加固定数目的存储位置
如:每次扩充增加10个元素位置,这种策略称为线性增长。
特点:节省空间,但是扩充操作频繁,操作次数多。
- 每次扩充容量加倍
如:每次扩容增加一倍的存储空间。
特点:减少了扩充操作的执行次数,但可能会浪费空间资源。是以空间换时间,推荐的方式
线程表的操作
线性表的常见操作有初始化、求表长、增删改查等。事实上,每种数据结构都至少要有这几种操作,大部分的基础算法题都是基于此扩展的
线性表的操作如下
数组的概念
数组是线性表最基本的结构,特点是元素是一个紧密在一起的序列。相互之间不需要记录彼此的关系就能访问。
数组中要注意的点
- 数组下标从0开始记录
- 例:第一个存储元素的位置是a[0],最后一个元素位置是a[length - 1]
- 数组中的元素在内存中是连续存储的,且每个元素占用着相同大小的内存
- 数组空间不一定是满的
- 例:空间为100的数组,可能只用了10个位置(数组中的元素数量),所以要注意数据个数的变量是size,数组长度length 可能不一样。
数组存储元素的特征
数组存储元素的过程
- 一,我创建了一个大小为10的数组,请问此时数组里面是什么?
- 答: 不同的语言处理会不一样,在c语言里每个位置都是一个随机数。而在java里,默认会初始化为0。而python更为灵活可以直接指定是什么,例如a =[1,2,3,4],就是数组里有四个元素,而a = [O for i in range(10)]这样定义的数组就是[0,0,0,0,0,,0,0,0, 0]
- 二: 是否可以只初始化一部分位置?
- 初始化的本质是什么?答: 当然可以,你可以将前面5个位置依次,后面的空着,此时数组内容为[1,2,3,4,5,0,0,0,0,0,1],初始化的本质就是覆盖已有的值,用你需要的值覆盖原来的0,因为数组本来是{0,0,0,0,0,0,0,0,0,0},这里只不过被你替换成了{1,2,3,4,5,0,0,0,0,0}。如果此时你想知道有效元素的个数,就必须再使用一个额外的变量,例如size来标记。
- 三.上面已经初始化的元素之间是否可以空着,例如初始化为{1,0,0,4,5,0,2,0,3,0}。其中0位置仍然是未初始化的?
- 答:不可以!绝对不可以!要初始化,就必须从前向后的连续空间初始化,不可以出现空缺的情况,这是违背数组的原则的。你正在进行某种运算期间可以先给部分位置赋值,而一旦稳定了,就不可以再出现空位置的情况。
- 四: 如果我需要的数据就是在中间某一段该怎么办呢? 例如r0,0,3,4,5,6,7,0,0,01,此时该怎么拿到从3到7的元素呢?
- 答:你需要使用两个变量,例如left=2,right=6来表示区间[left,right]是有效的。
- 五: 我删除的时候,已经被删除的位置该是什么呢? 例如原始数组为{1,2,3,4,5,6,7,8,0,01,我删除4之后,根据数组的移动原则,从5开始向前移动变成{1,2,3,5,6,7,8,?,0,0},那原来8所在的位置应该是什么呢?
- 答:仍然是8,也就是删除4之后的结构为(1,2,3,5,6,7,8,8,0,0},此时表示元素数量的size会减1变成7,原来8的位置仍然是8。因为我们是通过size来标记元素数量的,所以最后一个8不会被访问到。
- 第六炮: 这个里8看起来很不爽啊,是否可以再优化一下?
- 答: 不爽就不爽,习惯就好!不用优化,优化了也没啥用
数组的基本操作
数组的重要性
为什么数组的题目特别多呢,因为很多题目本质就是查找问题,而数组是查找的最佳载体。很多复杂的算法都是为了提高查找效率的,例如二分查找、二叉树红黑树、B+树、Hash和堆等等。另一方面很多算法问题本质上都是查找问题例如滑动窗口问题、回溯问题、动态规划问题等等都是在寻找那个目标结果。
查找一个元素
进行等值的线性查找,题目:
如果数组是递增的,此时查找时如果相等 或者 当前位置元素比目标值更大就停下来,使用代码实现
实现代码
/**
* 如果数组是递增的,此时查找时如果相等 或者 当前位置元素比目标值更大就停下来,使用代码实现
* @param arr 给定的数组
* @param size 数组中以存在的元素长度
* @param element 待查找的元素
* @return 该元素
*/
public int findElement(int [] arr ,int size , int element){
for (int i = 0; i < size; i++) {
if (arr[i] == element){
return i;
}else if (arr[i] > element){
return -1;
}
}
return -1;
}增加一个元素
题目:
将给定的元素插入到有序的数组的对应位置中
实现方法一
/**
* 题目
* 将给定的元素插入到有序的数组的对应位置中
* @param arr 有序数组
* @param size 数组已经存储的元素数量(从1开始计算)
* @param element 要插入的元素
* @return 插入元素的下标
*/
public int addElementSequence(int [] arr , int size , int element){
// 判断边界
if (size >= arr.length){
return -1;
}
// 定义插入元素的下标
int index = size;
// 通过循环,找到比要插入元素小的位置,将下标赋值
for (int i = 0; i < size; i++) {
if (arr[i] > element){
index = i;
break;
}
}
// 元素往后移
for (int i = size; i > index ; i --) {
// 后移一个位置
arr[i] = arr[i--];
}
// 将下标为index的元素设为element
arr[index] = element;
return index;
}实现方法二
public int addElementSequenceFromEnd(int [] arr , int size , int element){
if (size >= arr.length){
return -1;
}
int index = 0;
for (int a : arr) {
if (a <= element){
index++;
}else {
arr[index] = element;
break;
}
}
return index;
}删除一个元素
题目:删除一个元素
代码实现
/**
* 删除一个元素
* @param arr 给定的数组
* @param size 数组中元素的个数
* @param element 要删除的元素
* @return 删除元素后数组的长度
*/
public int removeElement(int [] arr , int size , int element){
int index = -1;
// 如果存在,找到该元素,并设置该元素下标
for (int i = 0; i < size; i++) {
if (arr[i] == element){
index = i;
}
}
// 如果找到元素,index就不等于-1;如果没找到,就等于默认值-1,直接退出
if ( index != -1){
//
for (int i = index +1; i < size; i++) {
arr[i-1] = arr[i];
}
// 长度减一
size--;
}
return size;
}单调数组问题
题目:
判断一个数组是否是单调递增的
方法一
/**
* 题目
* 判断一个数组是否是单调递增的
* @param arrs 给定的数组
* @return 是/否 单调递增
*/
public boolean isMonotonic(int [] arrs){
return isSort(arrs,true)|| isSort(arrs,false);
}
public boolean isSort(int [] nums , boolean increasing){
int length = nums.length;
for (int i = 0; i < length - 1; i++) {
if (increasing){
if (nums [i] > nums[i+1] ){
return false;
}
}else {
if (nums[i] < nums[i+1]){
return false;
}
}
}
return true;
}方法二(优化):
public boolean isMonotonicByOntMethod(int [] arr){
boolean inc = true, dec = true;
for (int i = 0; i < arr.length -1; i++) {
if (arr[i] > arr[i+1]){
inc = false;
}
if (arr[i] < arr[i+1]){
dec = false;
}
}
// 如果是单调的 ,返回结果为true;如果不是单调的,返回结果为false
return inc || dec;
}题目:
给定一个潘旭数组和一个目标值,在数组中找打目标值,并党徽其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置
/**
* 题目:
* 给定一个潘旭数组和一个目标值,在数组中找打目标值,并党徽其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置
* @param nums 有序数组
* @param target 要插入数组中的目标值
* @return 目标值的索引
*/
public int searchInsert(int [] nums , int target){
int length = nums.length;
int left = 0 , right = length -1 , index = length;
while (left <= right){
int mid = ((right - left) / 2)+ left;
if (target <= nums [mid] ){
index = mid;
right = mid -1;
} else {
left = mid + 1;
}
}
return index;
}