【暑期每日一练】 day11

news2024/12/24 22:14:08

选择题

（1）

解析：

（2）

解析：

（3）

解析：

（4）

解析：

（5）

解析：

编程题

题一

描述

示例

提示

解析：

代码实现

题二

描述

输入描述：

输出描述：

示例

解析：

代码实现

总结

选择题

（1）

1、声明以下变量，则表达式: ch/i + (f*d – i) 的结果类型为（）

char ch;
int i;
float f;
double d;

A: char B: int C: float D: double
答案：D

解析：

基本数据类型的等级从低到高如下：char int long float double运算的时候是从低转到高的，表达式的类型会自动提升或者转换为参与表达式求值的最上级类型

（2）

2、关于代码的说法正确的是（）

#include <stdio.h>
int main()
{
    int x = -1;
    unsigned int y = 2;
    if (x > y)
    {
        printf("x is greater");
    } 
    else
    {
        printf("y is greater");
    } 
    return 0;
}

A: x is greater B: y is greater C: 依赖实现 D: 随机
答案：A

解析：

x是有符号数-1，内存中是全1，当有符号的x和无符号数进行比较时，x会隐式类型转换被当做无符号数，是一个很大的数，这时就选择A了

（3）

3、已知有如下各变量的类型说明，则以下不符合C语言语法的表达式是（）

int k, a, b;
unsigned int w = 5;
double x = 1.42;

A: x%3 B: w+=-20 C: k=(a=200,b=300) D: a+=a-=a=9
答案：A

解析：

A选项，取余操作两边必须是整数

（4）

4、下面函数的输出结果是（）

void func()
{
    int k = 1^(1 << 31 >> 31);
    printf("%d\n", k);
}

A: 0 B: -1 C: -2 D: 1
答案：C

解析：

(1 << 31 );左移31位，并在右侧填充0，得到0x80000000，即符号位为1，其他为0，即-2147483648

int k = 1^(1 << 31 >> 31);注意，这里在右移的时候，符号位保持为1，右移后填充1，结果为0xFFFFFFFF，即-1，0x00000001^0xFFFFFFFF，即0xFFFFFFFE(-2)

（5）

5、如下代码的输出结果是（）

#include <stdio.h>
int main()
{
    int i = 1;
    sizeof(i++);
    printf("%d\n", i);
    return 0;
}

A: 1 B: 4 C: 2 D: 8
答案：A

解析：

一般表达式的运算是在运行时执行的，而sizeof是一个编译阶段就执行的运算符，在其内的任何运算都不执行，只推测出其中表达式结果的类型求其大小，故前后i的值不变。

编程题

题一

描述

给定一个二进制数组 nums ，计算其中最大连续 1 的个数

示例

提示

解析：

这道题思路比较简单，统计连续1的个数，遇到0时表示连续中断，判断如果当前的统计数大于之前最大的则替换，然后继续下一个位置开始的统计即可。

代码实现

int findMaxConsecutiveOnes(int* nums, int numsSize)
{
    int max_count = 0, cur_size = 0;;
    for (int i = 0; i < numsSize; i++) 
    {
        if (nums[i] == 1) 
        {
            cur_size++;
        }
        else 
        {
            max_count = max_count > cur_size ? max_count : cur_size;
            cur_size = 0;
        }
    }
    max_count = max_count > cur_size ? max_count : cur_size;
    return max_count;
}

题二

描述

完全数（Perfect number），又称完美数或完备数，是一些特殊的自然数。

它所有的真因子（即除了自身以外的约数）的和（即因子函数），恰好等于它本身。

例如：28，它有约数1、2、4、7、14、28，除去它本身28外，其余5个数相加，1+2+4+7+14=28。

输入n，请输出n以内(含n)完全数的个数。

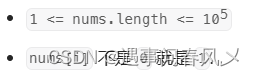
数据范围： 1≤n≤5×105

输入描述：

输入一个数字n

输出描述：

输出不超过n的完全数的个数

示例

解析：

这道题的关键在于完全数的判断：完全数指的是一个数字的所有约数的和和自身相等。我们只需要从 1 开始将这个数的约数相加求和即可。

约数就是能够被数字整除，而这里简化的一个思路是数字能够被整除，则除数和结果就都是约数，这种思路下，只需要从1计算到平方根即可

比如：数字 8 ，能够整除 2 ，结果是 4 ，则除数 2 和结果 4 都是约数，而这两个只需要一次计算判断即可。

需要注意的是 4，9，25... 这种，除数和结果相同的情况，则除数或者结果只相加一次就够了。

代码实现

#include <stdio.h>
#include <math.h>
int is_perfect_num(int num) {
    int sum = 1;
    for (int i = 2; i <= sqrt(num); i++) 
    {
        if (num % i ==0) 
        {//判断是否能够整除i，能整除则i和结果都是约数
            sum += i; //与除数相加
            if (i != sqrt(num))//防止除数和结果相同的情况下重复相加
                sum += num / i; //与相除结果相加
        }
    }
    if(sum == num) 
        return 1;
    return 0;
}
int main() 
{
    int n;
    while (~scanf("%d", &n)) 
    {
        int count = 0;
        for (int i = 2; i <= n;i++) 
        { //对n以内的数字都进行判断是否是完全数，注意1不参与判断
            if (is_perfect_num(i)) count++;
        }
        printf("%d\n", count);
    } 
    return 0;
}