​✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机  电力系统

⛄ 内容介绍

在这项研究中，开发了基于供需优化 (SDO) 算法的改进版本，这是一种最近开发的元启发式搜索方法。为了在 SDO 中更有效地模拟供需过程，使用适合度-距离平衡 (FDB) 方法确定了指导搜索过程的候选解决方案。为了测试和验证所开发的基于 FDB 的 SDO 算法的性能，使用了现代基准套件 CEC 2017。该套件有四种不同类型和三十个无约束测试问题。这些问题被设计成30/50/100维，以测试和验证所提算法在不同类型和维数的搜索空间中的性能。此外，二十个工程设计问题被用来测试和验证所提出的 FDBSDO 变体在受约束的工程设计问题中的性能。使用非参数统计测试方法分析来自两项实验研究的数据。根据分析结果，FDBSDO 变体在所有实验研究中都显示出优于基本算法的性能，具有约束/无约束、单模态/多模态/混合/组合问题类型和不同维度。FDB选择方法的实现消除了SDO算法的早熟收敛问题。所提出的 FDBSDO 算法具有敏感搜索的能力，有效地提供多样性，并在开发探索之间建立强大的平衡。使用非参数统计测试方法分析来自两项实验研究的数据。根据分析结果，FDBSDO 变体在所有实验研究中都显示出优于基本算法的性能，具有约束/无约束、单模态/多模态/混合/组合问题类型和不同维度。FDB选择方法的实现消除了SDO算法的早熟收敛问题。所提出的 FDBSDO 算法具有敏感搜索的能力，有效地提供多样性，并在开发探索之间建立强大的平衡。使用非参数统计测试方法分析来自两项实验研究的数据。根据分析结果，FDBSDO 变体在所有实验研究中都显示出优于基本算法的性能，具有约束/无约束、单模态/多模态/混合/组合问题类型和不同维度。FDB选择方法的实现消除了SDO算法的早熟收敛问题。所提出的 FDBSDO 算法具有敏感搜索的能力，有效地提供多样性，并在开发探索之间建立强大的平衡。具有约束/无约束、单峰/多峰/混合/组合问题类型和不同维度。FDB选择方法的实现消除了SDO算法的早熟收敛问题。所提出的 FDBSDO 算法具有敏感搜索的能力，有效地提供多样性，并在开发探索之间建立强大的平衡。具有约束/无约束、单峰/多峰/混合/组合问题类型和不同维度。FDB选择方法的实现消除了SDO算法的早熟收敛问题。所提出的 FDBSDO 算法具有敏感搜索的能力，有效地提供多样性，并在开发探索之间建立强大的平衡。

⛄ 部分代码

function index = rouletteFitnessDistanceBalance( population, fitness )

[~, bestIndex] = min(fitness); 

best = population(bestIndex, :);

[populationSize, dimension] = size(population);

distances = zeros(1, populationSize); 

normFitness = zeros(1, populationSize); 

normDistances = zeros(1, populationSize); 

divDistances = zeros(1, populationSize);

if (min(fitness) == max(fitness)) || (sum(fitness) >= Inf) || ~(sum(best)< inf)

    index = randi(populationSize);

    

else

    for i = 1 : populationSize

        value = 0;

        for j = 1 : dimension

            value = value + abs(best(j) - population(i, j));

        end

        distances(i) = value;

    end

    minFitness = min(fitness); maxMinFitness = max(fitness) - minFitness;

    minDistance = min(distances); maxMinDistance = max(distances) - minDistance;

    for i = 1 : populationSize

        normFitness(i) = 1 - ((fitness(i) - minFitness) / maxMinFitness);

        normDistances(i) = (distances(i) - minDistance) / maxMinDistance;

        divDistances(i) = normFitness(i) + normDistances(i);

    end

    r = rand * sum(divDistances);

    c = cumsum(divDistances);

    index = find( r <= c, 1, 'first');

end

end

⛄ 运行结果

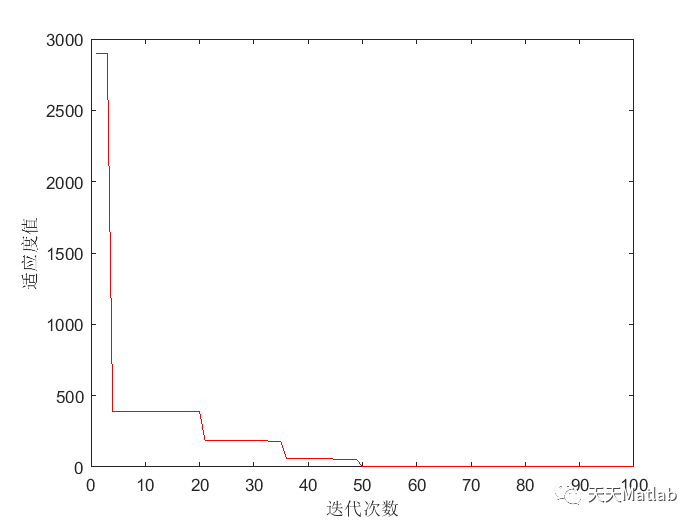
⛄ 参考文献

Katı, M., Kahraman, H. T. (2020). Improving Supply-Demand-Based Optimization Algorithm with FDB Method: A Comprehensive Research on Engineering Design Problems, Journal of Engineering Sciences and Design (Mühendislik Bilimleri ve Tasarım Dergisi), doi: 10.21923/jesd.829508, 8(5), 156-172, 2020.

Katı, M , Kahraman, H . (2020). ARZ-TALEP TABANLI OPTİMİZASYON ALGORİTMASININ FDB YÖNTEMİ İLE İYİLEŞTİRİLMESİ: MÜHENDİSLİK TASARIM PROBLEMLERİ ÜZERİNE KAPSAMLI BİR ARAŞTIRMA . Mühendislik Bilimleri ve Tasarım Dergisi , Özel Sayı: Uluslararası Mühendislikte Yapay Zeka ve Uygulamalı Matematik Konferansı (UMYMK 2020) , doi: 10.21923/jesd.829508, 156-172 . Retrieved from https://dergipark.org.tr/tr/pub/jesd/issue/58118/829508

⛄ Matlab代码关注

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料