一)全排列:

46. 全排列 - 力扣（LeetCode）

1)先画出决策树:

越详细越好，就是我们在进行暴力枚举这道题的过程中，如何不重不漏地将所有的情况全部枚举到，把这个思想历程给画下来，就可以了，把每一步的决策树画出来

 

2)设计代码: 

2.1)设计全局变量:就需要看一下这个递归过程中要记录一些什么东西

a)使用一个二维数组在这个题就是保存我们最终的返回值

b)使用一个一维数组int[] path来保存此时路径上的所有的选择，path的作用就是当我在对这棵树做深度优先遍历的时候，记录一下此时路径上的所有选择，遍历到到叶子节点的时候就可以将这个path加入到二维数组中(path.length==nums.length)，

但是向上回溯的时候还需要恢复现场的，就拿最上面的那一个图来说，当我遍历到最下面的123的时候，需要将123这个数存放到二维数组里面，但是向上归上一层的过程中，要把3去掉，再次向上一层归的时候，要把2干掉；

c)此时再来想一下剪枝操作该如何来进行实现呢，此时就需要一个布尔数组，这个布尔数组就是用来帮助我们进行记录这个数是否已经在这个路径中使用过了，布尔数组里面记录下标，判断一下当前这个下标所对应的数是否已经在当前被使用过了

d)所以当我们选择2的时候，我们就应该将布尔类型的1设置成true，意思就是1位置的这个2已经被我使用过了，然后再去遍历当前数组

for(int i=1;i<=3;i++) if(bol[i]==true) path.add(array[i])

2.2)设计dfs函数:仅仅只需要关心某一个节点在干啥即可

就是将整个数组所有的数给枚举一遍如果这个数没有用到过的话，就把这个数放到path后面

2.3)细节问题:

a)回溯:回溯在进行向上归的时候，要把最后一个数给干掉

b)剪枝:向上回溯到上一层的过程中，要把这个数在check数组中重新标记成false

c)递归出口:当我们遇到叶子节点的时候，直接添加结果

写这个递归时候的一个小技巧:在我们进行编写回溯代码的时候，只需要关心每一层在做什么事情即可，只需要写出每一层中相同的函数逻辑即可

class Solution {
    List<List<Integer>> ret;
    List<Integer> path;
    boolean[] bool;
    public List<List<Integer>> permute(int[] nums) {
       ret=new ArrayList<>();
       path=new ArrayList<>();
       bool=new boolean[nums.length];
       dfs(nums);
       return ret;
    }
    public void dfs(int[] nums){
        //在我们的递归函数里面,我们只需要关心每一层在做什么事情就可以了
        if(path.size()==nums.length){
            ret.add(new ArrayList<>(path));
            return;
        }
      for(int i=0;i<nums.length;i++){
          if(bool[i]==false){
              path.add(nums[i]);
        bool[i]=true;
        dfs(nums);
        //回溯-->恢复现场
        bool[i]=false;
        path.remove(path.size()-1);
        }
      }
 }
}

二)子集:

78. 子集 - 力扣（LeetCode）

一)解法一:

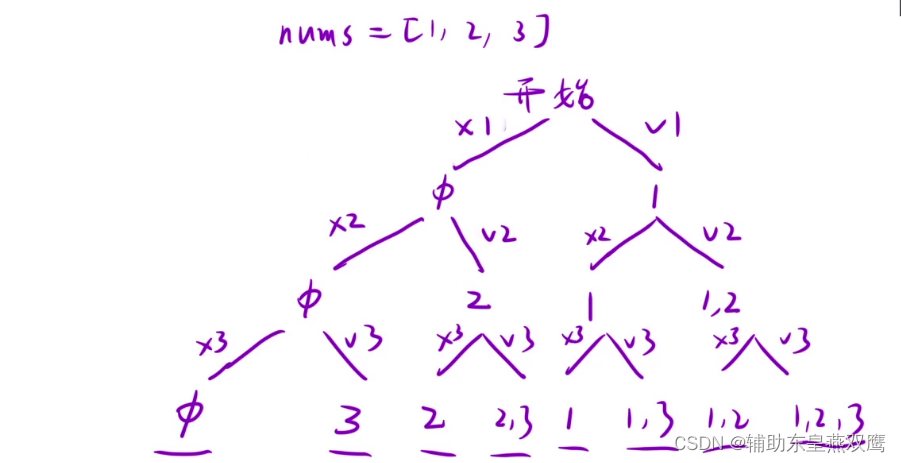
1)画出决策树:针对于当前元素是否进行选择画出决策树

1)全局变量的设计:

1)使用一个二维数组来保存我们最终计算出来的结果，里面的值保存的就是最终所有的路径

2)使用一个一维数组来保存每一个路径上面的所有字符串

2)dfs的设计:

2.1)我们每一层所做的事情就是不仅要进行传递nums，当进行考虑到每一个值的时候，都需要进行判断当前这个值是选择还是不选择，还需要知道当前我们遍历到了哪一个位置，传递的是这个数对应的下标，只需要考虑这个数选择还是不进行选择

2.2)如果选择了，那么就见这个数添加到path中

path.add(nums[i])

dfs(path，i+1)

如果不选，path终究不会添加任何数字，dfs(path，i+1)

3)细节问题

a)剪枝:

b)回溯:当进行回溯的时候，一定要记得恢复现场path.remove(nums[i])

c)递归出口:仅仅需要考虑到叶子节点的时候，就可以向上返回了当i等于nums.size()的时候

递归的出口也就是说什么时候收集结果

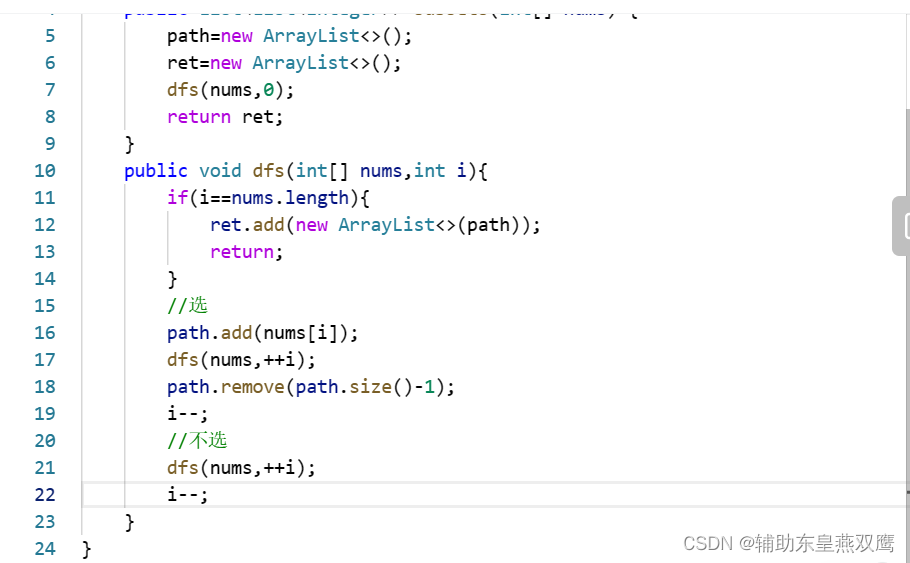
class Solution {
    List<Integer> path;
    List<List<Integer>> ret;
    public List<List<Integer>> subsets(int[] nums) {
        path=new ArrayList<>();
        ret=new ArrayList<>();
        dfs(nums,0);
        return ret;
    }
    public void dfs(int[] nums,int i){
        if(i==nums.length){
            ret.add(new ArrayList<>(path));
            return;
        } 
        //选
        path.add(nums[i]);
        dfs(nums,i+1);
        path.remove(path.size()-1);
        //不选,不选的话当前没有path路径中没有加这个数,所以也不需要恢复现场了
        dfs(nums,i+1);
    }
}

二)解法2:

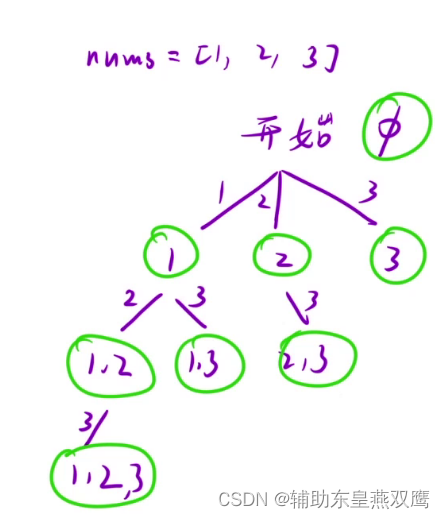
1)画决策树:针对于自己中含有0个元素，1个元素，2个元素来画出决策树，根据元素个数来进行设计决策树，当进行决策的时候只是考虑这个数后面的这个数

在上面的这个决策树中决策树中每一个结点的值都是我们想要的结果

2)设计代码:

a)全局变量:仍然搞一个二维数组来返回最终的结果，使用一维数组来存放最终的结果

b)dfs:找一找每一个节点都在做什么事情，都是从当前这个位置开始向后找到元素进行拼接只是把后面的数添加到path中

dfs(nums，pos):代表着你接下来一层要从哪里开始进行枚举

for(int i=pos；i<nums.length；i++)

{

path.add(nums[i])；

dfs(nums，i+1)；

//返回现场

path.remove(path.size()-1)；

}

c)细节问题，回溯剪枝递归出口:

回溯:进入到函数体的时候，都需要添加结果

class Solution {
    List<Integer> path;
    List<List<Integer>> ret;
    public List<List<Integer>> subsets(int[] nums) {
        this.path=new ArrayList<>();
        this.ret=new ArrayList<>();
        dfs(nums,0);
        return ret;
    }
    public void dfs(int[] nums,int index){
        ret.add(new ArrayList<>(path));
//在这里面我们只是进行考虑决策树上面的每一个节点都在干什么事情,index表示当前要传入元素的下一个位置
        for(int i=index;i<nums.length;i++){//i代表的是元素的下标
             path.add(nums[i]);
             dfs(nums,i+1);
             path.remove(path.size()-1);
        }
    }
}

三)