1 理解PID
先说结论:调整开关量让反馈更接近目标。
这里拿水龙头打比方,我们想控制水龙头的出水量为一半,这里就涉及两个关键量,阀门和出水量;阀门,即上面说的开关量;出水量即反馈;目标即一半的出水量;开关量的变化会让反馈随之变化。
实际操作是:我们慢慢打开阀门,即开关量在增加,同时出水量(反馈)也在增加;根据PID的算法,我们会一直将出水量与目标比较,当小于目标值时,会一直增加开关量,一当超过时就会减少开关量。
模型如下:
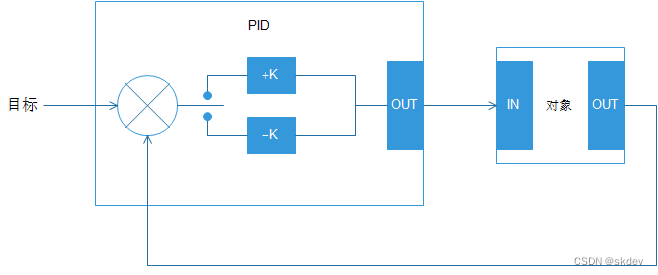
这里有一个很明显的特点:
开关量和反馈是不同的东西,单位不一样,并没有直接的关系,也就是说没有直接公式能表达出转换关系,反馈是通过传感器或检测装置测量得到的。
这里再打另一个比方,控制四轴无人机在空中悬停,这里涉及的变量有:4路电机动力的PWM和无人机水平的欧拉角,据据PID算法,哪个轴的角度偏低了就加大PWM占空比,偏高就减少PWM占空比。
从这里可以看出,欧拉角度和PWM占空比并没有直接的关系公式。这里只涉及,根据角度偏离目标多少来调节PWM占空比的方法。比如,当角度偏离大时,PWM占空比可以一点一点增加;也可以偏离大时增加很多,当偏离小时增加小点;这此曲线特点就是由P参数、I参数和D参数决定的。
2 PID公式

Kp、Ki和Kd是公式系数,不同的值会产生不同的接近曲线。
Out(t) 是当前产生的输出,即开关量,如果是用于PWM,那就是占空比,如果要产生0~100的值,就需要调整Kp、Ki和Kd的值。
t表示这是一个循环定时调用的函数。
e(t) 是当前反馈和目标差值
![]() 是差值累加
是差值累加
de(t) 是当前差值与上次差值的差值。
测试代码
#include <stdio.h>
#include <string.h>
#include <stdint.h>
typedef struct{
double target; // 设定目标Target value
double Kp; // 比例常数Proportional Const
double Ki; // 积分常数Integral Const
double Kd; // 微分常数Derivative Const
double last_error; // Error
double sum_error; // Sums of Errors
} _PID_t;
_PID_t PID; // PID Control Structure
double PIDCalc( _PID_t *pp, double feedback )
{
double dError, Error, Out;
Error = pp->target - feedback; // 偏差
pp->sum_error += Error; // 积分
dError = Error - pp->last_error; // 当前微分
pp->last_error = Error;
Out = (pp->Kp * Error // 比例项
+ pp->Ki * pp->sum_error // 积分项
+ pp->Kd * dError ); // 微分项
return Out;
}
void PIDTarget (_PID_t *pp, double target )
{
pp->target = target;
}
void PIDInit (_PID_t *pp)
{
memset ( pp,0,sizeof(_PID_t));
}
int main()
{
float speed = 0;
float result;
int i;
PIDInit ( &PID ); // Initialize Structure
PID.Kp = 2;
PID.Ki = 0.1;
PID.Kd = 0.0;
PIDTarget(&PID, 50.0); // Set target
speed = 0;
for(i=0;i<50;i++)
{
speed+=1;
result = PIDCalc(&PID,speed);
printf("%f %f\n",result,speed);
}
for(i=0;i<10;i++)
{
speed-=1;
result = PIDCalc(&PID,speed);
printf("%f %f\n",result,speed);
}
for(i=0;i<10;i++)
{
speed+=1;
result = PIDCalc(&PID,speed);
printf("%f %f\n",result,speed);
}
return 0;
}3 参数调试
从上面的分析可知,反馈和输出是不同单位的,两者并无直接关系。那么如何使输出符合开关量的范围?
3.1 Kp
Kp即P的系数,P全称是Proportional系数,比例的意思,即Error的系数。
![]()
target为目标值
![]() 为起始反馈值
为起始反馈值
![]() 为输出范围
为输出范围
假设#1,target = 50,![]() = 0,Kp = 0.04那么
= 0,Kp = 0.04那么 ![]() = 50*0.04 = 2,即feedback由0->50时,Out则输出2~0。
= 50*0.04 = 2,即feedback由0->50时,Out则输出2~0。

假设#2,target = 50, ![]() = 100,Kp = 0.04那么
= 100,Kp = 0.04那么![]() = -50*0.04 = -2,即feedback由0->50时,Out则输出-2~0。
= -50*0.04 = -2,即feedback由0->50时,Out则输出-2~0。

由上可知,可以通过Kp将输出的范围变化到开关量的范围内。比如PWM的占空比0~100,没有负数,只需用到假设#1,我们把Kp=2, ![]() = 50*2 = 100,范围就在0~100。
= 50*2 = 100,范围就在0~100。
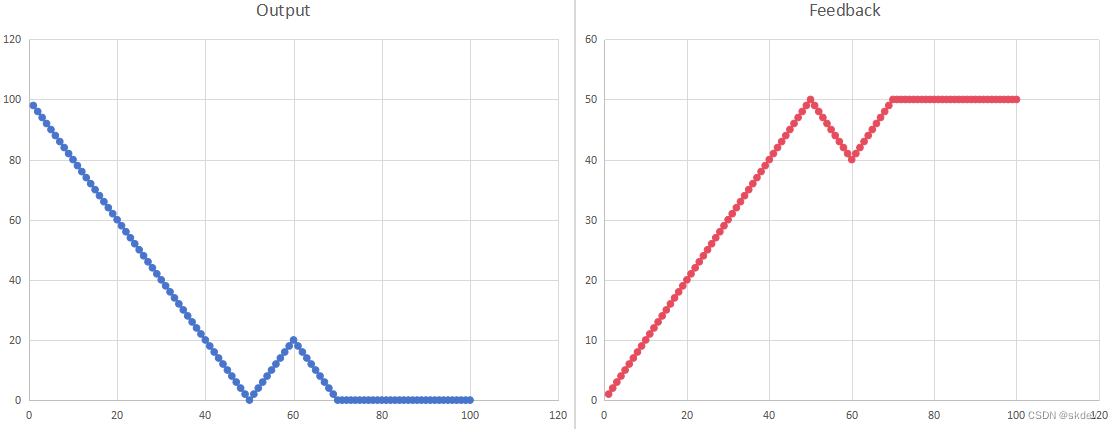
3.2 Ki
Ki即I的系数,I全称是Integral系数,积分的意思,即Error积分的系数。
target = 50,![]() = 0,则最大的sum_error =
= 0,则最大的sum_error = ![]() = 1275
= 1275
该系数起到的效果是快速或缓慢接近目标,其值由0.01开始往上调,根据自己的需求确认靠近速度。
在上调时注意曲线,其值大到一定程度时曲线会变形,所以不能过大。
3.3 Kd
Kd即D的系数,D全称是Derivative系数,积分,即dError微分的倍数。
从公式可以看出,Kd影响很小。
在Ki确定后,Kd也由0.01开始往上调,起到曲线微调作用。
4 实例调参
下面表格是pwm duty对应的电机转速:
| pwm duty | speed |
| 100 | 137 |
| 90 | 128 |
| 80 | 122 |
| 70 | 113 |
| 60 | 105 |
| 50 | 99 |
| 40 | 85 |
| 30 | 75 |
| 20 | 60 |
| 10 | 42 |
Speed的范围是0~137,那么缩放比例Kp = 100/137 = 0.73
Kp = 0.73, Ki = 0.1, Kd = 0.0, target = 60
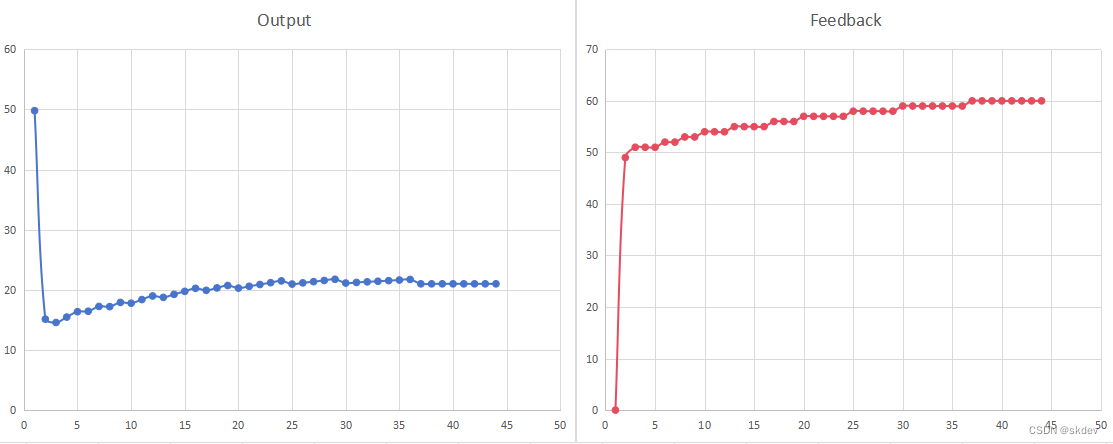 由上图可知,红线到达60时,时间轴是30
由上图可知,红线到达60时,时间轴是30
Kp = 0.73, Ki = 0.2, Kd = 0.0, target = 60
 由上图可知,红线到达60时,时间轴是12
由上图可知,红线到达60时,时间轴是12
Kp = 0.73, Ki = 0.3, Kd = 0.0, target = 60
 由上图可知,红线到达60时,时间轴是接近5
由上图可知,红线到达60时,时间轴是接近5
Kp = 0.73, Ki = 0.3, Kd = 0.01, target = 60
由上图可知,红线到达60时,时间轴是4
5提示
个人理解,可能有偏颇的地方。