4.2串的模式匹配

模式匹配：子串的定位操作称为串的模式，它求的是子串（常称模式串）在主串中的位置。

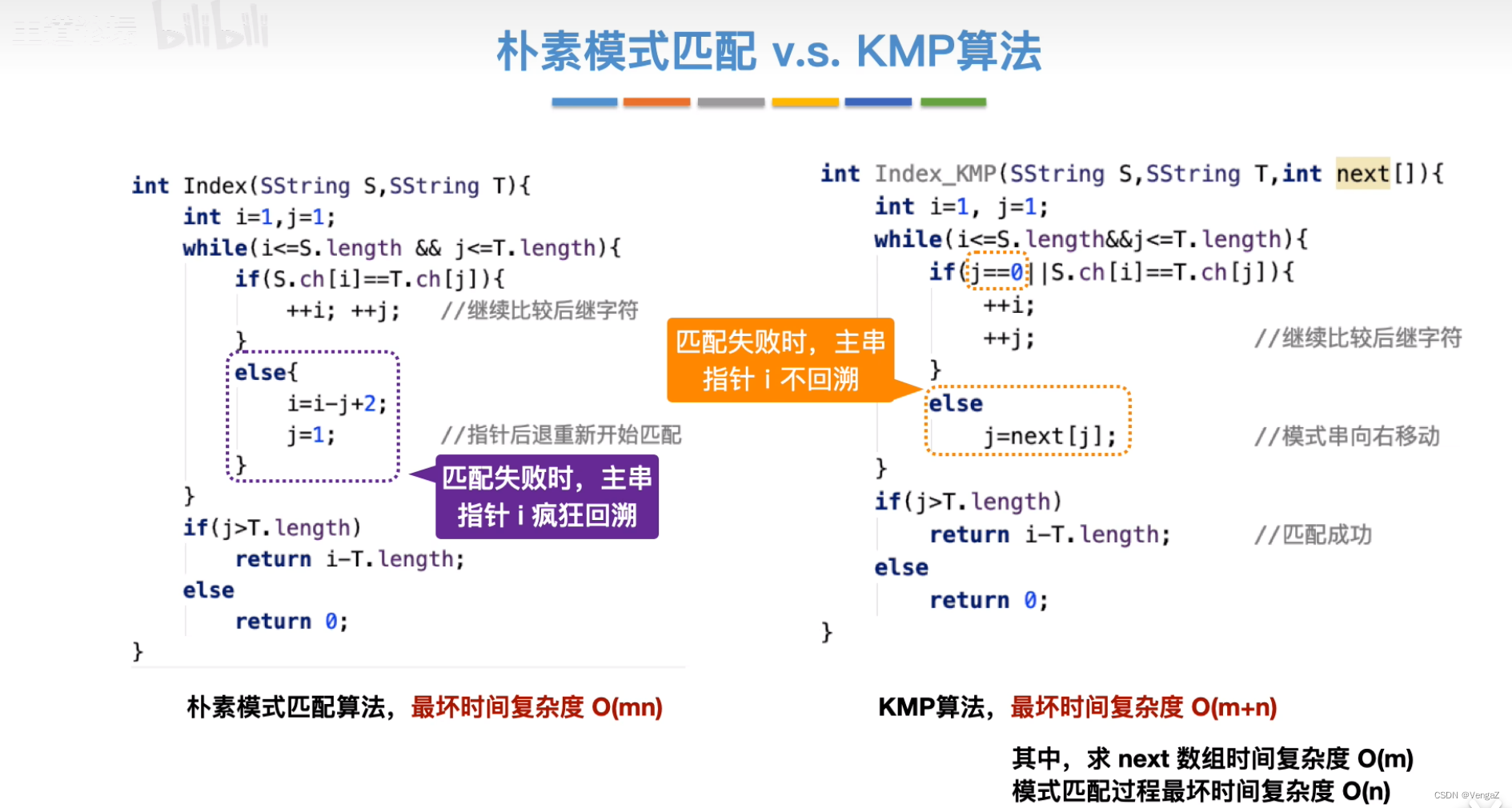
4.2.1朴素模式匹配算法

n-m+1主串中能有的串个数

int Index(SString S, SString T){
    int i=1;                //扫描主串S
    int j=1;                //扫描模式串T
    while(i<=S.length && j<=T.length){
        if(S.ch[i] == T.ch[j]){
            ++i;
            ++j;             //继续比较后继字符
        }
        else{
            i = i-j+2;  //回到这次匹配的第一个位置之前+1得到匹配的第一个位置
            //再+1才能得到下一次匹配的第一个位置
            j=1;             //指针后退重新开始匹配
        }
    }
    if(j>T.length)  //匹配成功，返回第一个字符位置
        return i-T.length;
    else
        return 0;
}

时间复杂度分析：

主串长度为n，模式串长度为m
最多比较n-m+1个子串

• 最坏时间复杂度 = O(nm)
  每个子串都要对比m个字符(对比到最后一个字符才匹配不上)，共要对比n-m+1个子串，复杂度 = O((n-m+1)m) = O(nm - m^2 + m) = O(nm)
  PS:大多数时候，n>>m
• 比较好时间复杂度 = O(n)
  每个子串的第一个字符就匹配失败，共要对比n-m+1个子串，复杂度 = O(n-m+1) = O(n)
  匹配一次就匹配成功：O（m）

4.2.2改进的模式匹配算法——KMP算法

不匹配的字符之前，一定是和模式串一致的；
根据模式串T，求出next数组（只与模式串有关，与主串无关），利用next数组进行匹配，当匹配失败时，主串的指针 i 不再回溯！
next数组是根据子串求出来的，当前面的字符串已知时如果有重复的，从当前的字符匹配即可。

1. 求next数组

• 作用：当模式串的第j个字符失配时，从模式串的第next[j]继续往后匹配;
• 对于任何模式串，当第1个字符不匹配时，只能匹配下一个子串，因此，next[1] = 0——表示模式串应右移一位，主串当前指针后移一位，再和模式串的第一字符进行比较；
• 对于任何模式串，当第2个字符不匹配时，应尝试匹配模式串的第一个字符，因此，next[2] = 1;

分界线后的第一个元素的位序就是next[j]的值

2. 利用next数组进行模式匹配

int Index_KMP(SString S, SString T, int next[]){
    int i=1;     //主串
    int j=1;     //模式串
    while（i<S.length && j<=T.length){
        if(j==0 || S.ch[i]==T.ch[j]){      //第一个元素匹配失败时
            ++j;
            ++i;         //继续比较后继字符
        }
        else
            j=next[j]   //模式串向右移动
    }
    if(j>T.length)
        return i-T.length; //匹配成功
}

3. 时间复杂度分析

• 求next数组时间复杂度 = O(m)
• 模式匹配过程最坏时间复杂度 = O(n)
• KMP算法的最坏时间复杂度 = O(m+n)

4.2.3 next数组的优化思路nextval，优化KMP

如果next[j]的值对应的模式串的值相等，则说明就算跳转到这个位置也一样匹配失败，所以nextval[j]的值就是next[j]的值减一，再判断还会不会一样。

概括

数据结构：串模式匹配与KMP算法及其优化

在计算机科学中，字符串匹配是一种常见的操作，即在一个文本串中查找一个模式串是否存在，并返回其位置或匹配的结果。串模式匹配涉及到多种算法，其中KMP算法是一种经典且高效的字符串匹配算法。本文将对串模式匹配及KMP算法进行介绍，并讨论其优化方法。

串模式匹配

串模式匹配是指在一个文本串（主串）中查找一个给定的模式串是否存在的问题。在实际应用中，字符串匹配是一个非常常见的操作，例如在文本编辑器中查找关键词、在搜索引擎中搜索相关内容等。在字符串匹配中，最简单的方法是暴力匹配，即从文本串的每个位置开始，逐个字符与模式串进行比较。但暴力匹配算法的时间复杂度较高，特别是在文本串和模式串较长的情况下。

KMP算法

KMP算法是一种高效的字符串匹配算法，它利用模式串自身的特性，在匹配过程中跳过一些无需比较的字符，从而减少比较的次数，提高匹配效率。KMP算法的核心是利用部分匹配表（Partial Match Table，简称PMT）来记录模式串的前缀和后缀的最长公共子串长度，从而决定在匹配过程中模式串的移动位置。

KMP算法的过程

1. 构建部分匹配表（PMT）：首先计算模式串的每个前缀的最长公共前后缀的长度，得到部分匹配表PMT。
2. 匹配过程：从文本串的第一个字符开始，与模式串的第一个字符进行比较。
3. 匹配失败：如果比较的字符不相等，则利用PMT中记录的信息来确定模式串的移动位置，跳过一部分无需比较的字符。
4. 匹配成功：如果比较的字符相等，则继续比较下一个字符，直到模式串全部匹配成功或者文本串结束。

KMP算法的优势

相较于暴力匹配算法，KMP算法具有以下优势：

• 减少比较次数：KMP算法利用部分匹配表，避免了一些无需比较的字符，减少了比较次数，提高了匹配效率。
• 避免回溯：KMP算法在匹配失败时，不需要回溯到文本串的前一个位置，而是根据PMT中的信息，直接移动模式串，避免了重复比较。

KMP算法的优化

虽然KMP算法已经是一个高效的字符串匹配算法，但在某些特殊情况下，仍然可以进行进一步的优化。以下是一些KMP算法的优化方法：

1. 优化部分匹配表（PMT）的构建： 在构建PMT时，可以利用模式串自身的特性，避免重复计算最长公共前后缀的长度，从而减少构建PMT的时间复杂度。

2. 改进KMP算法的移动方式： 在匹配失败时，KMP算法利用PMT来决定模式串的移动位置，可以考虑优化移动方式，使得匹配过程更加高效。

3. 应用多模式匹配算法： 如果需要同时匹配多个模式串，可以考虑使用多模式匹配算法，如AC自动机算法，来进一步提高匹配效率。

结论

串模式匹配是计算机科学中一个常见且重要的问题，而KMP算法作为一种高效的字符串匹配算法，在实际应用中具有广泛的用途。通过对KMP算法的优化，可以进一步提高匹配效率，使得字符串匹配操作更加高效和可靠。无论是在文本编辑器、搜索引擎还是其他应用中，串模式匹配与KMP算法的应用都能够为我们带来更好的用户体验和效果。