先放结论
- 对于一个无向连通图1:
- 存在欧拉路径的充分必要条件为:度数为奇数的点只有 0 0 0 或 2 2 2 个。
- 存在欧拉回路的充分必要条件为:没有度数为奇数的点。
- 对于一个有向连通图:
- 存在欧拉路径的充分必要条件为:
- 所有点的入度等于出度。
- 一个点(起点)的出度比入度大 1 1 1,一个点(终点)的入度比出度大 1 1 1,其余点入度出度数量相等。
- 存在欧拉路径的充分必要条件为:所有点的入度等于出度。
- 存在欧拉路径的充分必要条件为:
必要条件的证明
显然,上面的结论都是欧拉路径(欧拉回路)的性质,所以必然成立。因此这些结论都是存在欧拉路径的必要条件。
充分条件的证明
先看两种情况:
-
对于有一个公共点的线和环,如下图所示:
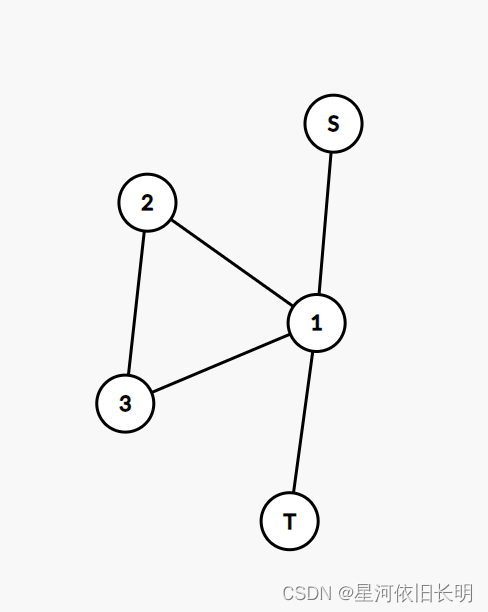
此时的欧拉路径为: S → 1 → 3 → 2 → T S \rightarrow 1 \rightarrow 3 \rightarrow 2 \rightarrow T S→1→3→2→T -
对于有一个公共点的两个环,如下图所示:
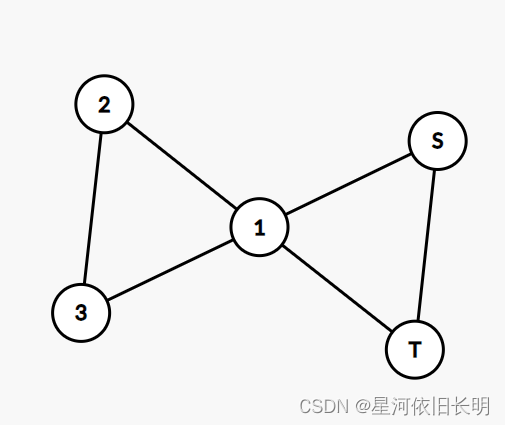
此时的一种可行欧拉路径为: S → 1 → 3 → 2 → T S \rightarrow 1 \rightarrow 3 \rightarrow 2 \rightarrow T S→1→3→2→T
那此时一个图就可以看作一条路径和附着在这条路径上的若干个环。
于是我们得出:对于除了起点与终点外的点,由于它们的度数是偶数,则只要它从某一个过环出发,则必然会走完这个环回到这个点。
合并环的方法:有环先走环
证毕。
求欧拉路径
使用算法:DFS
以下是伪代码:
dfs(u)
{
for 从 u 出发的所有边
dfs(edge[u]) 扩展
把 u 加入序列 seq[] ← u
}
执行后 seq[] 就是欧拉路径。
接下来考虑怎么标记访问过的边。
- 对于有向图,每用一条边就删掉
- 对于无向图,每用一条边标记对应的反向边(进行 Xor 操作)
这里连通图定义为所有边都能相互到达。在欧拉回路与欧拉路径中,允许存在孤立的点。有向图的“连通”与此相同。 ↩︎