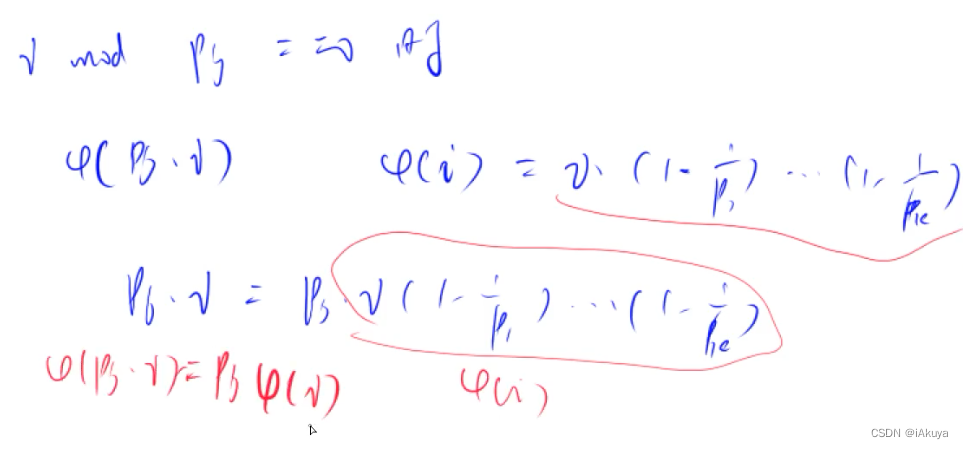题目

给定一个正整数n，求1~n中每个数的欧拉函数之和。

输入格式

共—行，包含一个整数n。

输出格式

共一行，包含一个整数，表示1~n中每个数的欧拉函数之和。

数据范围

1 ≤n ≤106

• 输入样例:

6

• 输出样例:

12

题解

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1000010;
int primes[N], cnt;
int phi[N];
bool st[N];
LL get_eulers(int n)
{
	phi[1] = 1;
	for ( int i = 2; i <= n; i ++ )
	{
		if ( lst[ i])
		{
		primes[ cnt ++ ]= i;
		phi[ i] = i - 1;
		}
		for (int j = 0; primes[j] <= n / i; j ++)
		{
			st[ primes[j]* i] = true;
			if ( i % primes[j] == 0)
			{
				phi [ primes[j]* i] = phi[ i]* primes[ j];
				break;
			}
			phi[primes[j]* i]= phi[ i]* (primes[j] - 1);
		}
	}
	LL res = 0;
	for ( int i = 1; i <= n; i ++ ) res += phi[ i];
	return res;
}
int main()
{
int n;
cin >> n;
cout << get_eulers(n) << endl;
return 0;
}

思路

本题运用之前的线性筛选法，加上如下图的推导即可