题目

思路

一眼bfs
为了保证bfs能够绕一个圈，我们将这个联通块的最下面的点的下方割去，如图

绿色的地方就是割去的地方，然后我们再加个判断，使bfs从起点出发转一圈，再把这条分割线的左右两边步数最小连起来，就出答案了
理论存在，实践开始

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=55;
int dx[]={-1,-1,-1,0,0,1,1,1};
int dy[]={-1,0,1,-1,1,-1,0,1};
int n,m;
char a[maxn][maxn];
int d[maxn][maxn];
int p,q;
queue<pair<int,int> > Q;
void bfs(){
	memset(d,-1,sizeof(d));
	for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(a[i][j]=='*') d[i][j]=0,Q.push(make_pair(i,j));
	while(!Q.empty()){
		auto [x,y]=Q.front();Q.pop();
		for(int k=0;k<8;k++){
			int xx=x+dx[k],yy=y+dy[k];
			if(y==q&&x>=p&&(k==2||k==4||k==7)) continue;
			if(y==q+1&&x>=p) if(x==p) { if(k==5) continue; } else if(k==0||k==3||k==5) continue;
			if(a[xx][yy]=='.'&&d[xx][yy]==-1) d[xx][yy]=d[x][y]+1,Q.push(make_pair(xx,yy));
		}
	}
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i]+1;
	for(int i=n;i&&!p;i--) for(int j=1;j<=m;j++) if(a[i][j]=='X') { p=i,q=j;break; }
	bfs();
	int ans=1<<30;
	for(int i=p+1;i<=n;i++) for(int j=-1;j<=1;j++) if(d[i][q]!=-1&&d[i+j][q+1]!=-1) ans=min(ans,d[i][q]+d[i+j][q+1]+1);
	cout<<ans;
	return 0;
}

dx,dy的说明

(dx[0],dy[0]):左上
(dx[1],dy[1]):上
(dx[2],dy[2]):右上
(dx[3],dy[3]):左
(dx[4],dy[4]):右
(dx[5],dy[5]):左下
(dx[6],dy[6]):下
(dx[7],dy[7]):右下

如何才能让bfs不过分割线

首先看第一个判断

if(y==q&&x>=p&&(k==2||k==4||k==7)) continue;

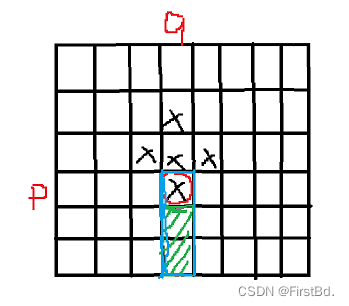
蓝色部分为判断范围，如果说搜到这个判定范围，就判断一下是否是向右走，若是就跳过，来保证bfs顺时针转而不过分割线

if(y==q+1&&x>=p) if(x==p) { if(k==5) continue; } else if(k==0||k==3||k==5) continue;

这个情况是bfs已经绕了一圈到分割线右侧

end

完结撒花