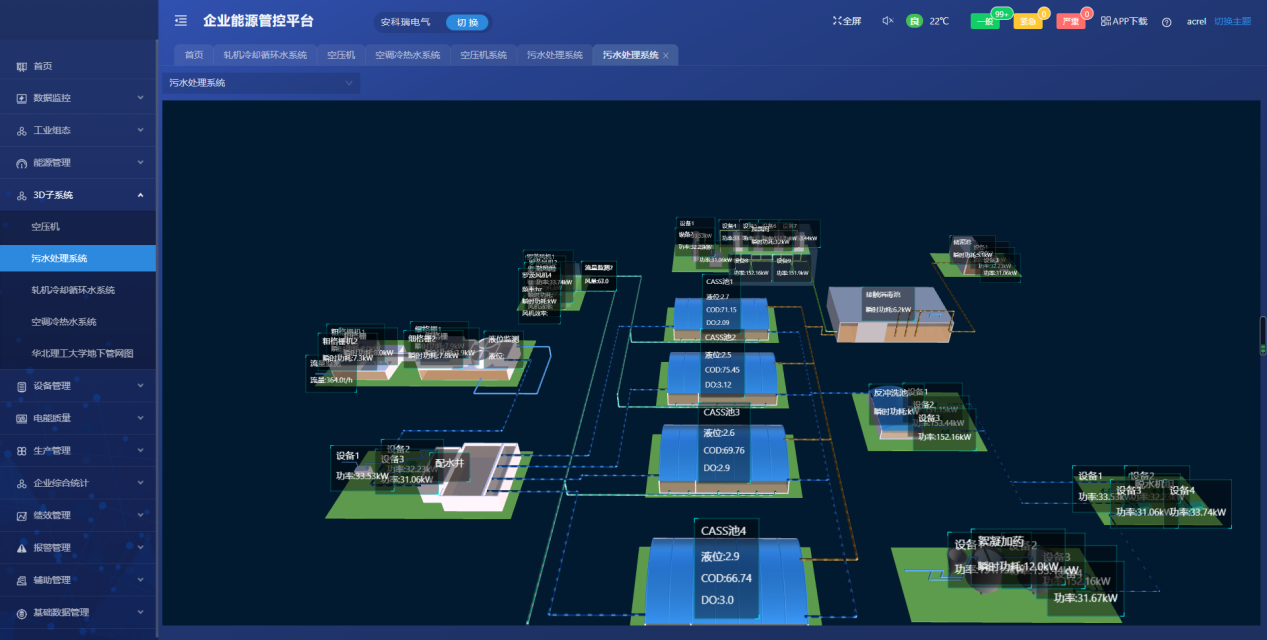
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
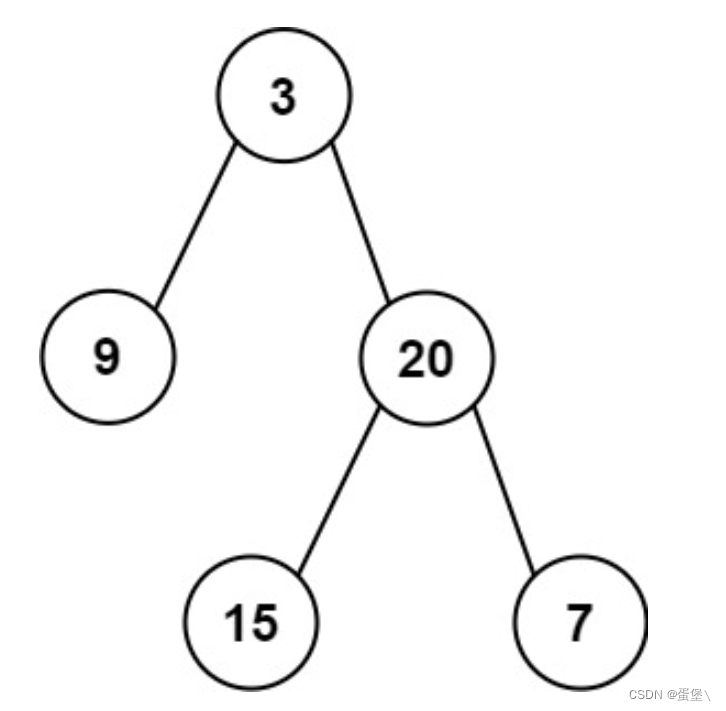
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]
源代码如下:
递归:
/* 解题思路:
1.通过先序遍历的特点我们可以确定地是根节点永远是先序序列的第一个值
2.先分别划分左子树和右子树节点在先序序列和中序序列中的下标范围
3.因为我们要在中序序列中找到根节点的下标,所以我们通过哈希表建立中序序列中的节点值和下标的映射关系
//index[inorder[i]]=i;
4.在中序遍历中找到根节点的位置后,可以确定的是根节点之前的节点都是左子树上的节点,根节点之后的节点是右子树上的节点,所以我们根据下标关系确认左子树的节点总数leftnode
5.不断更新左子树在先序和中序序列中的左右边界和右子树在先序和中序序列中的左右边界
6.左子树上的所有节点的下标范围(先序序列中):[preo_left,preo_right]
左子树上的所有节点的下标范围(中序序列中):[ino_left,ino_right]
7.右子树也是同理
8.递归地构造节点的左子树和右子树
*/
class Solution {
public:
unordered_map<int,int> index;
TreeNode* dfs(vector<int>& preorder, vector<int>& inorder,int preo_left,int preo_right,int ino_left,int ino_right)
{
if(preo_left>preo_right) return nullptr;
//找到根节点在中序遍历中的下标
int in_root_index=index[preorder[preo_left]];
//根节点永远是先序序列的左边界
TreeNode* root=new TreeNode(preorder[preo_left]);
//左子树的节点总数为中序序列中根节点的下标-中序遍历的左边界
int leftnode=in_root_index-ino_left;
//注意左右边界的表示
root->left=
dfs(preorder,inorder,preo_left+1,preo_left+leftnode,ino_left,in_root_index-1);
root->right=
dfs(preorder,inorder,preo_left+leftnode+1,preo_right,in_root_index+1,ino_right);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n=preorder.size();
//建立节点值与下标的映射关系
for(int i=0;i<n;i++)
{
index[inorder[i]]=i;
}
//初始时边界都为[0,n-1]
return dfs(preorder,inorder,0,n-1,0,n-1);
}
};迭代:
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if(preorder.size()==0) return nullptr;
stack<TreeNode*> st;
TreeNode* root=new TreeNode(preorder[0]);//根节点是先序遍历的第一值
st.push(root);//将根节点入栈
int inorder_index=0;//中序序列从起始位置开始
//开始除根节点之外的其他节点的遍历
for(int i=1;i<preorder.size();i++)
{
int pre_val=preorder[i];
TreeNode* node=st.top();//栈顶元素就是根节点
//因为在中序序列中,根节点将左右子树分开了
//所以,如果中序序列当前的值不是根节点,说明这个值是左子树上的,就入栈
if(node->val!=inorder[inorder_index])
{
//创建左子树上的节点
node->left=new TreeNode(pre_val);
st.push(node->left);
}
//如果找到根节点了
else
{
//节点出栈,直到找到第一个有右子树的根节点
while(!st.empty()&&st.top()->val==inorder[inorder_index])
{
node=st.top();//记录根节点
st.pop();//节点出栈
inorder_index++;//中序序列上的节点不断更新
}
//找到了,就创建右子树上的节点
node->right=new TreeNode(pre_val);
st.push(node->right);
}
}
return root;
}
};时间复杂度:O(n)
空间复杂度:O(n)