目录
一,题目
二,堆排序
1、堆排序基本介绍
2、堆排序基本思想
3、堆排序步骤图解说明
四,总结堆排序的整体思路
五,整体代码实现
1.普通版
2,STL版
一,题目
给定你一个长度为 n 的整数数列。
请你使用快堆排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式
输入共两行,第一行包含整数 n。
第二行包含 n 个整数(所有整数均在 1∼10^9 范围内),表示整个数列。
输出格式
输出共一行,包含 n 个整数,表示排好序的数列。
数据范围
1≤n≤100000
输入样例:
7 2 1 5 4 3 2 0输出样例:
0 1 2 2 3 4 5
二,堆排序
1、堆排序基本介绍
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(n*logn),它也是不稳定排序。
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆, 注意 : 没有要求结点的左孩子的值和右孩子的值的大小关系。
每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆(此题用小顶堆)
另外要注意,此题的堆要用数组来储存
小顶堆举例:
从中可发现,编号为i的节点的左孩子编号为i * 2,右孩子编号为i * 2 + 1
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2] // i 对应第几个节点,i从1开始编号
大顶堆举例:

我们对堆中的结点按层进行编号,映射到数组中就是下面这个样子:
大顶堆特点:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] // i 对应第几个节点,i从1开始编号
一般升序采用大顶堆,降序采用小顶堆
2、堆排序基本思想
堆排序基本思想是:
将待排序序列构造成一个小顶堆
此时,整个序列的最大值就是堆顶的根节点。
将其与末尾元素进行交换,此时末尾就为最大值。
然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
可以看到在构建大顶堆的过程中,元素的个数逐渐减少,最后就得到一个有序序列了
3、堆排序步骤图解说明
比如就拿样例中的{2 1 5 4 3 2 0}举例
step 1:将这些数加入小顶堆中
 ->
-> ->
-> ->
-> ->
->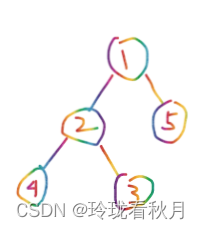 ->
-> ->
->
对应代码:
void hpush(int k)
{
int now = ++hsiz,nxt;
//now:k不断“上浮”时的位置 nxt:now将要“上浮”到的位置,也就是now的父节点的编号
heap[now] = k;//讲k插入该堆中
while(now > 1)//只要k没“上浮”到根的位置
{
nxt = now / 2;//计算出now的父节点的编号
if(heap[now] < heap[nxt])//只要现在仍能“上浮”
{
swap(heap[now],heap[nxt]);//“上浮”
now = nxt;
}
else break;//不能上浮,则跳出
}
}
step 2:一个个取出小顶堆的根(即数列中的最小值),并输出和继续维护该小顶堆
先把堆顶0取出,并输出,再让堆数组的末尾2来替补:

但是这样并不是一个小顶堆,所以需要对2进行“下沉”操作,直至移动至正确位置:
然后重复step 2,直到堆的大小为0。
对应代码:
int hpop()
{
int ans = heap[1],now = 1,nxt;//ans:小顶堆的根
heap[1] = heap[hsiz--];//拿堆数组末尾来替补已经被取出的根
while(2 * now <= hsiz)//只要now还有孩子
{
nxt = now * 2;//将nxt设为now的左孩子的编号
if((nxt + 1 <= hsiz) && (heap[nxt] > heap[nxt + 1])) nxt++;
//如果now的右孩子的编号<=堆的大小,说明now有右孩子。
//如果now有右孩子且右孩子<左孩子,则将判断是否要“下沉”的权利交给更小的右孩子。
if(heap[now] > heap[nxt])//判断是否可以“下沉”
{
swap(heap[now],heap[nxt]);//下沉
now = nxt;
}
else break;//不可以则跳出来
}
return ans;
}四,总结堆排序的整体思路
1).将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
2).将堆顶元素与末尾元素交换,将最大元素"下沉"到数组末端:
3).重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤
直到整个序列有序。
五,整体代码实现
1.普通版
#include<bits/stdc++.h>
using namespace std;
int n,tmp,ny,heap[100001],hsiz;
void pr()
{
for(int i = 1;i <= hsiz;i++) cout<<heap[i]<<" ";
cout<<endl;
}
void hpush(int k)
{
int now = ++hsiz,nxt;
heap[now] = k;
while(now > 1)
{
nxt = now / 2;
if(heap[now] < heap[nxt])
{
swap(heap[now],heap[nxt]);
now = nxt;
}
else break;
}
}
int hpop()
{
int ans = heap[1],now = 1,nxt;
heap[1] = heap[hsiz--];
while(2 * now <= hsiz)
{
nxt = now * 2;
if((nxt + 1 <= hsiz) && (heap[nxt] > heap[nxt + 1])) nxt++;
if(heap[now] > heap[nxt])
{
swap(heap[now],heap[nxt]);
now = nxt;
}
else break;
}
return ans;
}
int main()
{
cin>>n;
while(n--)
{
cin>>tmp;
hpush(tmp);
//pr();
}
while(hsiz) cout<<hpop()<<" ";
return 0;
}
/*
7
2 1 5 4 3 2 0
*/2,STL版
#include <bits/stdc++.h>
using namespace std;
int sie,a[10000001];
void f(int n)
{
a[++sie] = n;
push_heap(a + 1,a + 1 + sie,greater<int>());
}
int pop()
{
pop_heap(a + 1,a + 1 + sie,greater<int>());
return a[sie--];
}
int main()
{
int g,t;
cin>>t;
for(int i = 0;i < t;i++)
{
cin>>g;
f(g);
}
while(t--) cout<<pop()<<" ";
return 0;
}