目录
题目:
背景:
方法一:暴力递归 复杂度O(2^N)
方法二:复杂度O(N)
方法三:O(logN)复杂度
两个矩阵相乘:
求矩阵m的p次方的代码实现:
用矩阵乘法求斐波那契数列第N项代码实现:
题目:
给定整数N,返回斐波那契数列的第N项。
背景:
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)。
方法一:暴力递归 复杂度O(2^N)
public static int f1(int n) {
if (n < 1) {
return 0;
}
if (n == 1 || n == 2) {
return 1;
}
return f1(n-1) + f1(n-2);
}方法二:复杂度O(N)
从左到右依次求出每一项的值:
(1)定义三个变量 result,pre,tmp
(2)tmp 保存上次的result值 (用于等会儿赋值给pre),然后计算新的result=result+pre,计算完新的result之后,把tmp中存的上一个result的值赋值给pre。换句话说,就是实现前一个和后一个一直相加。
//从左到右依次求出每一项的值 1 1 2 3 5 8 13 ...
public static int f2(int n) {
if (n < 1) {
return 0;
}
if (n ==1 || n==2) {
return 1;
}
int result = 1;
int pre = 1;
int tmp = 0;
//返回的结果 result 一直是result和pre(上一个result)相加
for (int i = 3; i <=n; i++) {
tmp = result;
result = result + pre; //与前一个结果相加(pre)
pre = tmp; //把上一个result的值赋值给pre
}
return result;
}方法三:O(logN)复杂度
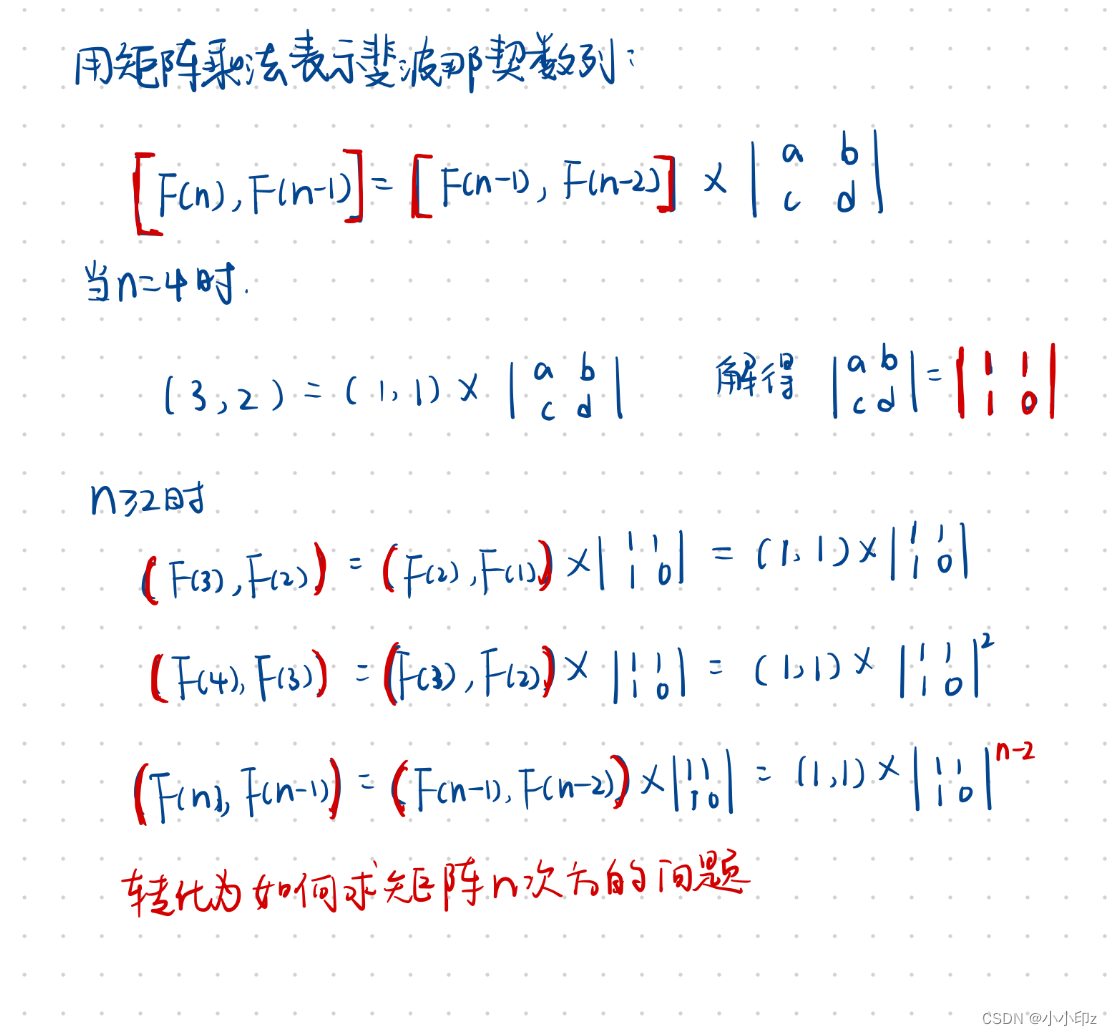
先看如何求整数的N次方,例如求10的75次方:
(1)75的二进制数形式为 1001011
(2)10的75次方 = 10^64 * 10^8 * 10^2 * 10^1
先求10^1,再根据10^1求10^2,再根据10^2求10^4,……,最后根据10^32求10^64,然后最后把10^64 * 10^8 * 10^2 * 10^1 相乘。
两个矩阵相乘:
注意:
初始化一个数组 int[][] arr = new int[2][3] ,那么arr.length就是2(行数),arr[0].length就是3(列数),arr[1].length也是3。
示例:
初始化两个二维数组,m1是int[2][3],m2是[3][2],相乘得到的res数组是2*2的
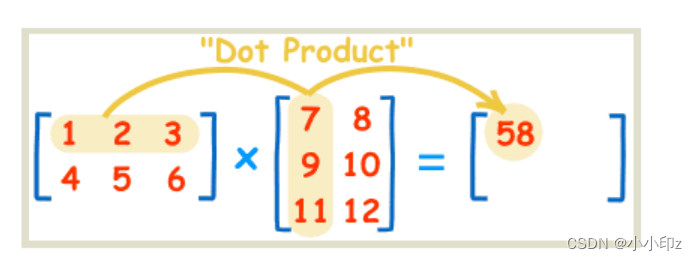
计算过程:
左边矩阵的每一行,分别去乘右边矩阵的每一列,对应位置相乘相加。
代码实现:
//两个矩阵相乘的具体体现
public int[][] muliMatrix(int[][] m1, int[][] m2) {
int [][] res = new int[m1.length][m2[0].length]; //m1 的行数 和m2的行数
//按行遍历 m1
for(int i = 0; i < m1.length; i++) {
//按列遍历 m2
for (int j = 0; j < m2[0].length; j++) {
//遍历对应位置相乘相加
for (int k = 0; k < m2.length; k++) {
res[i][j] += m1[i][k] * m2[k][j];
}
}
}
return res;
}测试代码:
public static void main(String[] args) {
int[][] m1 = {{1,2,3},{4,5,6}};
int[][] m2 = {{7,8},{9,10},{11,12}};
int[][] ints = muliMatrix(m1, m2);
System.out.println(Arrays.deepToString(ints));
}测试结果:
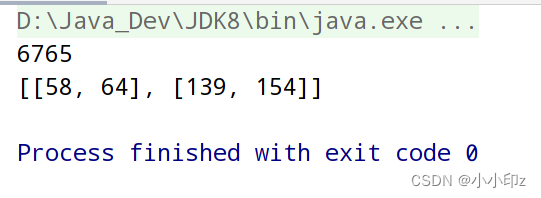
求矩阵m的p次方的代码实现:
只有方阵才能求幂
过程解析:
(1)初始化res大小,和m大小一样。
(2)先将res设置为单位阵,相当于整数中的1。
(3)tmp来保存需要求幂的矩阵
(4)for循环遍历,知道p为0停止
在for循环中:
p >> 1代表p右移一位,就是p除以2
如果p是奇数,p & 1=1,如果p是偶数 p & 1=0
先判断 p 是不是奇数,如果是奇数,就让 res = tmp * res
以p = 11为例,求m矩阵的11次幂:
1)p是奇数11,res = tmp * res(一次幂),tmp = tmp * tmp(相当于先求了一个二次幂)。
2) p右移除以2为5,res = tmp *res(此时相当于3次幂),tmp=tmp*tmp(现在tmp是4次幂)
3)p右移除以2为2,tmp=tmp*tmp(现在tmp是8次幂)
4)p右移除以2为1,res=res*tmp(此时相当于11次幂,已求够),tmp=tmp*tmp(16次幂)
5)p为0 循环结束 ,返回res。
总之,每次循环 tmp的次幂都会翻倍,11次幂,翻倍到 2,4,8,还差三次,需要执行三次if语句里面的。
代码实现:
//矩阵m的p次方
public static int[][] matrixPower(int[][] m, int p) {
int[][] res = new int[m.length][m[0].length];
//先把res设为单位矩阵(对角线为1) 相当于整数中的1
for (int i = 0; i < res.length; i++) {
res[i][i] = 1;
}
int[][] tmp = m; //m赋值给tmp
// p >>= 1 代表p右移一位赋值给p 右移一位相当于除以2 左移一位相当于乘以2
for (; p != 0; p >>= 1) {
//判断 p是不是偶数 如果p是奇数 p&1=1,如果p是偶数,p&1=0
if ((p & 1) != 0) {//p是奇数的时候
res = muliMatrix(res, tmp); //调用矩阵相乘的函数
}
tmp = muliMatrix(tmp, tmp);
}
return res;
}用矩阵乘法求斐波那契数列第N项代码实现:
解释最后为什么返回 res[0][0] + res[1][0]:
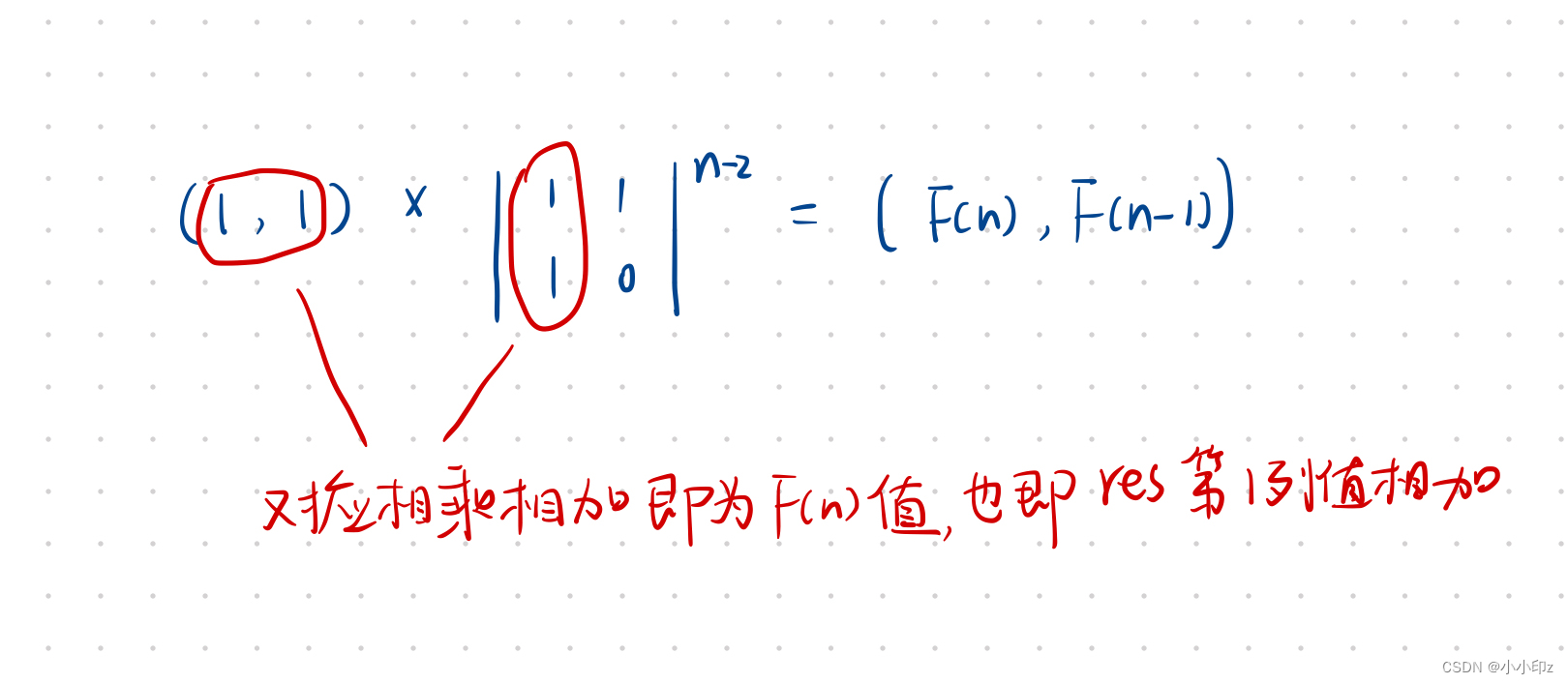
public static int f3(int n) {
if (n < 1) {
return 0;
}
if (n == 1 || n == 2) {
return 1;
}
int[][] base = {{1,1},{1,0}};
int[][] res = matrixPower(base, n-2);
return res[0][0] + res[1][0];
}