八大排序算法--冒泡排序（动图理解）

news2024/11/16 6:00:56

冒泡排序

算法思路

冒泡排序的原理是：从左到右，相邻元素进行比较。每次比较一轮，就会找到序列中最大的一个或最小的一个。这个数就会从序列的最右边冒出来。

以从小到大排序为例，第一轮比较后，所有数中最大的那个数就会浮到最右边；第二轮比较后，所有数中第二大的那个数就会浮到倒数第二个位置……就这样一轮一轮地比较，最后实现从小到大排序。

动画演示

算法代码

 public static void bubbleSort(int[] a){
    for (int i = 0; i < a.length-1; i++) {//a.length-1是因为不用与自己比较，所以比的数就少一个
         for (int j = 0; j < a.length-1-i; j++){//a.lenght-1-i是因为每一趟就会少一个数比较
             if(a[j]>a[j+1]){
                  int tmp = a[j];
                  a[j] = a[j+1];
                  a[j+1]  = tmp;
             }
         }
     }
  }

上面代码还有些不足，如果一个序列本来就有序，或者在排序的中间部分就已经排好序。但冒泡排序仍然会走完两个for循环，时间复杂度一直为O(n^2) 。为此我们可以改进代码，在每次比较开始前，都加一个flag标记，若交换了数，则改变flag,说明序列还未有序。若在一趟比较完后，flag没变，则说明序列已经有序，就不用再进行循环了。此时时间复杂度最好可变为O(n)。

优化后

 public static void bubbleSort(int[] a){

        for (int i = 0; i < a.length-1; i++) {
            int flag = 0;  //添加标记
            for (int j = 0; j < a.length-1-i; j++) {
                if(a[j]>a[j+1]){
                    int tmp = a[j];
                    a[j] = a[j+1];
                    a[j+1]  = tmp;
                    falg++;
                }
            }
            if(flag==0) break; //即falg在经过for循环后，还为0 说明已排好序了，就不用再进行排序
        }                      
    }

复杂度分析

时间复杂度 O(n^2) 优化后最好情况变为 o(n)

时间复杂度测试

接下来我们试着用大量数据测试一下。

int[] a = new int[10_0000]; //10万个数据测试

1.orderArray函数实现生成一个基本有序数列，即从小到大排列。

public static void orderArray(int[] a) {
        for (int i = 0; i < a.length; i++) {
            a[i] = i;
        }
 }

2.notOrderArray函数生成一个倒序数列，即从大到小排列。

public static void notOrderArray(int[] a) {
        for (int i = 0; i < a.length; i++) {
            a[i] = a.length-i;
        }
}

3.randomArray函数生成一个随机无序数列。

 public static void randomArray(int[] a) {
        Random random = new Random();
        for (int i = 0; i < a.length; i++) {
            a[i] = random.nextInt(10_0000);
        }
 }

4.testInsertSort函数测试 System.currentTimeMillis() 返回值单位是毫秒。

 public static void testInsertSort(int[] a){
        int[] tmpArray = Arrays.copyOf(a,a.length);
        long startTime = System.currentTimeMillis();    //注意用long接收
        shellSort(tmpArray);
        long endTime = System.currentTimeMillis();  //返回单位是毫秒
        System.out.println("冒泡排序耗时："+(endTime-startTime));
 }

5.main函数调用执行

public static void main(String[] args) {
 
 
        int[] a = new int[10_0000];
        //有序
        System.out.println("基本有序数列");
        orderArray(a);
        testInsertSort(a);
 
        //倒序
        System.out.println("逆序数列");
        notOrderArray(a);
        testInsertSort(a);
 
        //随机乱序
        System.out.println("无序数列");
        randomArray(a);
        testInsertSort(a);
 
}

运行结果

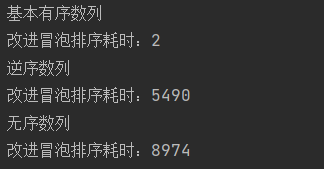
通过比较，发现改进后的时间复杂度还是有所下降的。

完整代码

import java.util.Random;

public class sort {

    public static void main(String[] args) {
    
        int[] a = new int[10_0000];
        
        //有序
        System.out.println("基本有序数列");
        orderArray(a);
        testInsertSort(a);

        //无序
        System.out.println("逆序数列");
        notOrderArray(a);
        testInsertSort(a);

        //乱序
        System.out.println("无序数列");
        randomArray(a);
        testInsertSort(a);

    }


    //冒泡排序
    //时间复杂度 O(n^2)   优化后 最好情况 O(n)
    public static void bubbleSort(int[] a){
        for (int i = 0; i < a.length; i++) {
            for (int j = 0; j < a.length-1-i; j++) {
                if(a[j]>a[j+1]){
                    int tmp = a[j];
                    a[j] = a[j+1];
                    a[j+1]  = tmp;
                }
            }
        }
    }


    //优化后的冒泡排序
    public static void bubbleSort1(int[] a){

        for (int i = 0; i < a.length; i++) {
            int flag = 0;
            for (int j = 0; j < a.length-1-i; j++) {
                if(a[j]>a[j+1]){
                    int tmp = a[j];
                    a[j] = a[j+1];
                    a[j+1]  = tmp;
                    flag++;
                }
            }
            if(flag==0) break;
        }
    }


    //生成有序数组  从小到大排列
    public static void orderArray(int[] a) {
        for (int i = 0; i < a.length; i++) {
            a[i] = i;
        }
    }


    //n无序 其实就是从大到小排列
    public static void notOrderArray(int[] a) {
        for (int i = 0; i < a.length; i++) {
            a[i] = a.length-i;
        }
    }

    //乱序 随机生成序列
    public static void randomArray(int[] a) {
        Random random = new Random();
        for (int i = 0; i < a.length; i++) {
            a[i] = random.nextInt(10_0000);
        }
    }

    //大量数据测试
    public static void testInsertSort(int[] a){
        int[] tmpArray = Arrays.copyOf(a,a.length);
        long startTime = System.currentTimeMillis();    //注意用long接收
        bubbleSort1(tmpArray);
        long endTime = System.currentTimeMillis();
        System.out.println("改进冒泡排序耗时："+(endTime-startTime));
    }

}