复杂度和简单排序算法
- 1,时间复杂度
- 1.1选择排序
- 1.2冒泡排序
- 1.3异或运算
- 1.3.1性质:
- 1.3.2案例
- 例1
- 例2
- 1.4插入排序
- 1.5二分法
- 1.5.1在一个有序数组中,找某个数是否存在
- 1.5.2在一个有序数组中,找>=某个数最左侧的位置
- 1.5.3局部最小值问题
- 1.6对数器的概念和使用
- 1.7递归方法和master公式
- 1.7.1递归方法
- 1.7.2master公式
1,时间复杂度

常数时间操作:加减乘除等少量运算
时间复杂度:在常数操作数量级的表达式中,不要低阶项,只要高阶项,而且忽略系数
大O算法时间复杂度
100N2+90万N:他的时间复杂度为O(N2)
时间复杂度按最差情况估计
1.1选择排序
时间复杂度O(N ^ 2),额外空间复杂度O(1)
#include<iostream>
#include<algorithm>
using namespace std;
void selectSort(int arr[], int n)
{
for (int i = 0; i < n; i++)
{
//寻找[i,n)区间里的最小值
int minIndex = i;
for (int j = i + 1; j < n; j++)
{
if (arr[j] < arr[minIndex])
{
minIndex = j;//更新索引
}
}
//找到最小位置的索引,然后交换最小位置的数和当前的位置的数
swap(arr[i], arr[minIndex]);
}
}
int main() {
int a[10] = { 10,15,20,1,2,3,6,45,21,22 };
selectSort(a, 10);
for (int i = 0; i < 10; i++)
{
cout << a[i] << " ";
}
cout << endl;
return 0;
}
1.2冒泡排序
时间复杂度O(N ^ 2),额外空间复杂度O(1)
#include <iostream>
using namespace std;
int main()
{
int arr[10] = { 10,50,40,60,80,20,30,70,0,90 };
int length = sizeof(arr) / sizeof(arr[0]);
for (int i = 0; i < length - 1; i++)
{
for (int j = 0; j < length - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
swap(arr[j], arr[j + 1]);
}
}
}
for (int i = 0; i < length; i++)
{
cout << arr[i] << " ";
}
cout << endl;
system("pause");
return 0;
}
1.3异或运算
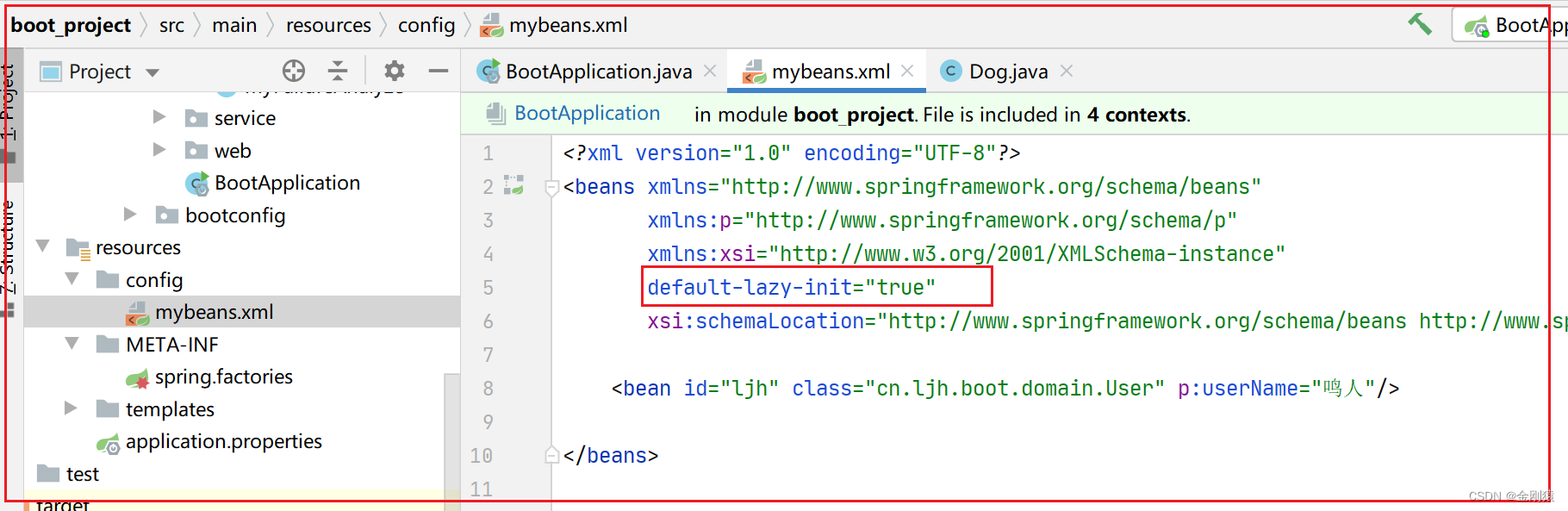
相同为0,不同为1
1.3.1性质:
0 ^ N == N
N ^ N == 0
异或运算满足交换律和结合律
a ^ b=b ^ a
a ^ b ^ c=a ^ (b ^ c)
一堆数和一个值异或时和顺序无关,无论顺序如何结果是一样的
a=甲,b=乙
a=a ^ b; //a = 甲 ^ 乙 // b = 乙
b=a ^ b; //a = 甲 ^ 乙 // b = 甲 ^ 乙 ^ 乙 = 甲
a=a ^ b; //a = 甲 ^ 乙 ^ 甲 = 乙 // b = 甲
交换时可以不用额外申请一个空间
注意:使用的前提是两个对象在内存里是俩块独立的区域
例:下列代码中的j和j+1位置不可以在同一个位置,否则会清0这块内存
#include <iostream>
using namespace std;
int main()
{
int arr[10] = { 10,50,40,60,80,20,30,70,0,90 };
int length = sizeof(arr) / sizeof(arr[0]);
for (int i = 0; i < length - 1; i++)
{
for (int j = 0; j < length - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
arr[j] = arr[j] ^ arr[j + 1];
arr[j + 1] = arr[j] ^ arr[j + 1];
arr[j] = arr[j] ^ arr[j + 1];
}
}
}
for (int i = 0; i < length; i++)
{
cout << arr[i] << " ";
}
cout << endl;
system("pause");
return 0;
}
1.3.2案例
例1
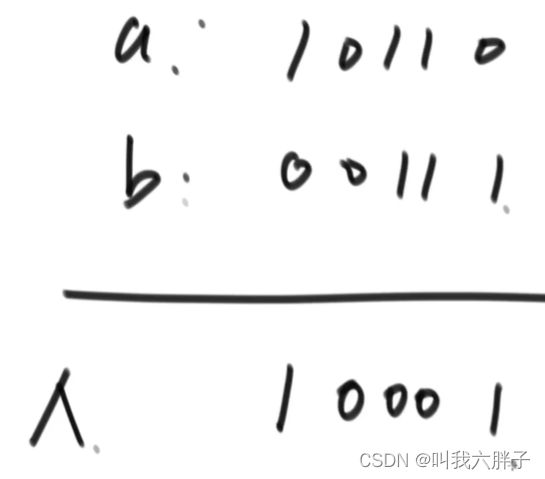
已知一种数出现奇数次,其他数出现偶数次,怎么找到出现奇数次的数
限定:时间复杂度O(N)、空间复杂度O(1)
答:用一个变量int eor=0
把eor从第一个数异或到最后一个数,最后eor为这个出现奇数次的数
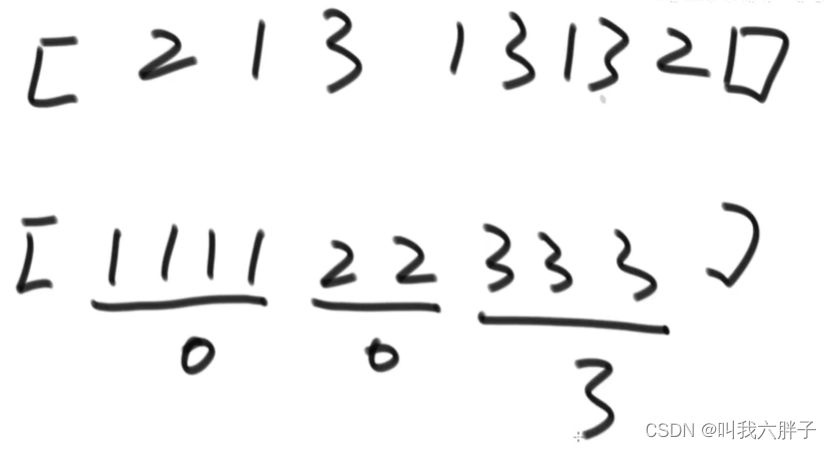
例2
已知两种数出现奇数次,其他数出现偶数次,怎么找到出现这两种数
限定:时间复杂度O(N)、空间复杂度O(1)
空间复杂度O(1)代表不会开辟新空间
答:用一个变量int eor=0,设出现奇数次的数为a和b,其他都为出现偶数次的数
用eor从第一个数异或到最后一个数,最后eor=a ^ b
因为是两种数,所以a!=b,所以eor!=0
再准备一个变量int eor‘=0,用eor’从第一个数异或到eor异或中偶数位上进行异或后不为0的整数(不存在异或状态),所以eor‘=a or b
所以a or b的另一个数=eor ^ eor’
#include <iostream>
#include <vector>
std::vector<int> findOddOccurrences(std::vector<int>& nums) {
int eor = 0; // 用于存储最终结果 a ^ b
for (int num : nums) {
eor ^= num; // 求异或
}
// 找到 a 和 b 不相同的位
int rightmostBit = eor & (-eor);
int eor1 = 0;
for (int num : nums) {
if ((num & rightmostBit) != 0) {
eor1 ^= num;
}
}
int eor2 = eor ^ eor1;
return { eor1, eor2 };
}
int main() {
std::vector<int> nums = { 2, 2, 4, 4, 5, 5, 3, 6, 6, 7 };
std::vector<int> result = findOddOccurrences(nums);
std::cout << "Numbers that appear odd number of times: " << result[0] << " and " << result[1] << std::endl;
return 0;
}
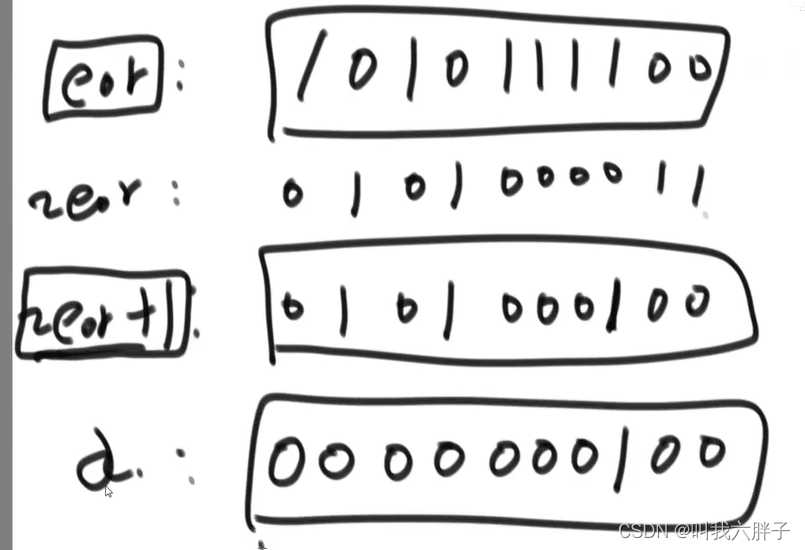
方法二
用一个变量int eor=0,设出现奇数次的数为a和b,其他都为出现偶数次的数
用eor从第一个数异或到最后一个数,最后eor=a ^ b
因为是两种数,所以a!=b,所以eor!=0
eor&(~eor+1)提取出最右边的1
1.4插入排序
7,6,5,4,3,2,1
最多排序次数1+2+3+4+5+6
时间复杂度O(N ^ 2),额外空间复杂度O(1)
1,2,3,4,5,6,7
最少排序次数0
时间复杂度按最差情况估计
arr[] = {3,2,5,4,2,3,3}
0到0号位变为有序
3和3比较,3
0到1号位变为有序
2和3比较,3大,2,3
2和自己比较,停
0到2号位变为有序
5和3比较,5大,2,3,5
0到3号位变为有序
4和5比较,5大,2,3,4,5
4和3比较,4大,停
0到4号位变为有序
2和5比较,5大,2,3,4,2,5
2和4比较,4大,2,3,2,4,5
2和3比较,3大,2,2,3,4,5
2和2比较,相同,停
0到5号位变为有序
3和5比较,5大,2,2,3,4,3,5
3和4比较,4大,2,2,3,3,4,5
3和3比较,相同,停
…………
#include <iostream>
void test01()
{
int arr[] = { 3,2,5,4,2,3,3 };
int length = sizeof(arr) / sizeof(arr[0]);
for (int i = 0; i < length ; i++)
{
for (int j = i; j >0; j--)
{
if (arr[j] < arr[j-1])
{
arr[j] = arr[j] ^ arr[j-1];
arr[j-1] = arr[j] ^ arr[j-1];
arr[j] = arr[j] ^ arr[j-1];
}
else
{
break;
}
}
}
for (int q = 0; q < length; q++)
{
std::cout << arr[q] << " ";
}
std::cout << std::endl;
}
int main()
{
test01();
return 0;
}
1.5二分法
时间复杂度O(log2N)(logN就是log2N),log3N等
1.5.1在一个有序数组中,找某个数是否存在
从小到大的有序数组,找num
如果采用遍历,时间复杂度为O(N)
二分法为O(log2N)(logN就是log2N)
先找到中点x,如果x>num则找左侧继续二分,如果x<num则找右侧继续二分
1.5.2在一个有序数组中,找>=某个数最左侧的位置
1.5.3局部最小值问题
arr中无序,相邻两数一定不相等
在0位置a,1位置b,a<b则a为局部最小
在end位置a,end-1位置b,b<a则b为局部最小
在N位置,N+1和N-1位置都比N大,则N为局部最小
找到一个局部最小数,时间复杂度好于O(N)与否?
先看0和1,N-2和N-1位置看大小,0或N-1小就直接输出了
0比1大,N-1比N-2大,那么0到N-1必定存在至少一个拐点
取中点M,看M-1和M-2位置比大小,如果最小直接输出
如果不是最小,那么比M小的一侧必有拐点,
一边小则在小的一边继续二分
两边小则随机取一边继续二分
体现了两种优化,数据状况,问题标准
1.6对数器的概念和使用
有一个想要测的方法a
实现复杂度不好但是容易实现的方法b
实现一个随机样本产生器
把方法a和方法b跑相同的随机样本,看看得到的结果是否一样
如果有一个随机样本使得对比结果不一致,打印样本进行人工干预,改对方法a或者方法b
当样本数量很多时比对测试依然正确,可以确定方法a已经正确
c++随机样本产生器
int randroom=rand()%999+2;
生成0+2到998+2的数值
// 对数器.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <vector>
#include <algorithm>
using namespace std;
//有一个你想要测试的算法,这里以归并排序为例
class Solution {
public:
static int reversePairs(vector<int>& nums) {
auto L = 0;
auto R = nums.size() - 1;
auto res = 0;
mergesort(nums, L, R);
return res;
}
//归并排序,从大到小排列(逆序)
static void mergesort(vector<int>& nums, int L, int R)
{
//递归终止条件
if (L >= R)
{
return;
}
//序列中心位置计算
auto mid = (L + ((R - L) >> 1));
//auto mid = (R + L) / 2;
//左右序列分别排序
mergesort(nums, L, mid);
mergesort(nums, mid + 1, R);
//归并两个排好序的序列
merge(nums, L, mid, R);
}
static void merge(vector<int>& nums, int L, int mid, int R)
{
//临时向量存储归并的结果
vector<int> tmp(R - L + 1);
auto pos = 0;
auto Lp = L;
auto Rp = mid + 1;
while ((Lp <= mid) && (Rp <= R))
{
tmp[pos++] = (nums[Lp] < nums[Rp]) ? nums[Lp++] : nums[Rp++];
}
while (Lp <= mid)
{
tmp[pos++] = nums[Lp++];
}
while (Rp <= R)
{
tmp[pos++] = nums[Rp++];
}
//将排序好部分拷贝至nums数组
copy(nums, tmp, L, R);
//nums = tmp;
}
//部分数组拷贝函数
static void copy(vector<int>& nums, vector<int>& tmp, int L, int R)
{
auto pos = 0;
for (auto i = L; i <= R; i++)
{
nums[i] = tmp[pos++];
}
}
};
//准备一个随机数组(样本)生成器
//函数名:generateRandomVector
//函数功能描述:随机数组(样本)生成器
//函数参数: size 生成数组最大尺寸
// value 数组每个元素的最大值
//返回值: vector<int> 生成的数组
//for test
vector<int> generateRandomVector(int size, int value)
{
//time 函数返回从 1970 年 1 月 1 日午夜开始到现在逝去的秒数,因此每次运行程序时,它都将提供不同的种子值。
srand((int)time(NULL));//为随机数生成器产生随机种子
//分配随机大小的数组,产生随机数的范围公式number = (rand()%(maxValue - minValue +1)) + minValue;
vector<int> result(rand() % (size + 1));
for (auto i = 0; i < result.size(); i++)
{
result[i] = rand() % (value + 1);
}
return result;
}
//大样本测试
//函数名:main
//函数功能描述:大样本测试
//函数参数: size 生成数组最大尺寸
// value 数组每个元素的最大值
//返回值: vector<int> 生成的数组
//for test
int main()
{
auto test_time = 50000;//测试次数,设置比较大,排除特殊情况
auto size = 10;//生成数组最大尺寸
auto value = 30;//生成数组每个元素的最大值
auto if_accept = true;//方法是否正确标志位
for(auto i = 0; i < test_time; i++)
{
//拷贝初始化,生成新的数组向量
vector<int> nums(generateRandomVector(size, value));
//生成两个临时数组拷贝
vector<int> nums1(nums);
vector<int> nums2(nums);
//绝对正确方法
sort(nums1.begin(), nums1.end());
//自己写的方法,想要测试的算法
Solution::reversePairs(nums2);
//判断两个向量是否相同,vector类已经重载了比较运算符,不用自己实现,不相同说明算法不正确
if(nums1 != nums2)
{
if_accept = false;
//输出结果不相等的原始向量
for(auto c: nums)
{
cout << c << " ";
}
break;
}
}
//输出结果
cout << (if_accept ? "nice!\n" : "false!\n");
}
1.7递归方法和master公式
1.7.1递归方法
目的:
递归行为和递归行为时间复杂度的估算
怎么用递归方法找一个数组中的最大值,系统是怎么操作的
递归基(base case):确定递归应该结束的条件,通常是问题规模达到最小的情况。
递归步骤(recursive step):将原问题分解为更小的子问题,并通过递归调用来解决这些子问题。
在使用递归时需要注意处理边界条件,避免无限递归和过深的递归栈
中点mid
mid=(L+R)/2,但是万一LR太大,可能会导致溢出,使结果变为负数出错
mid=L+(R-L)/2
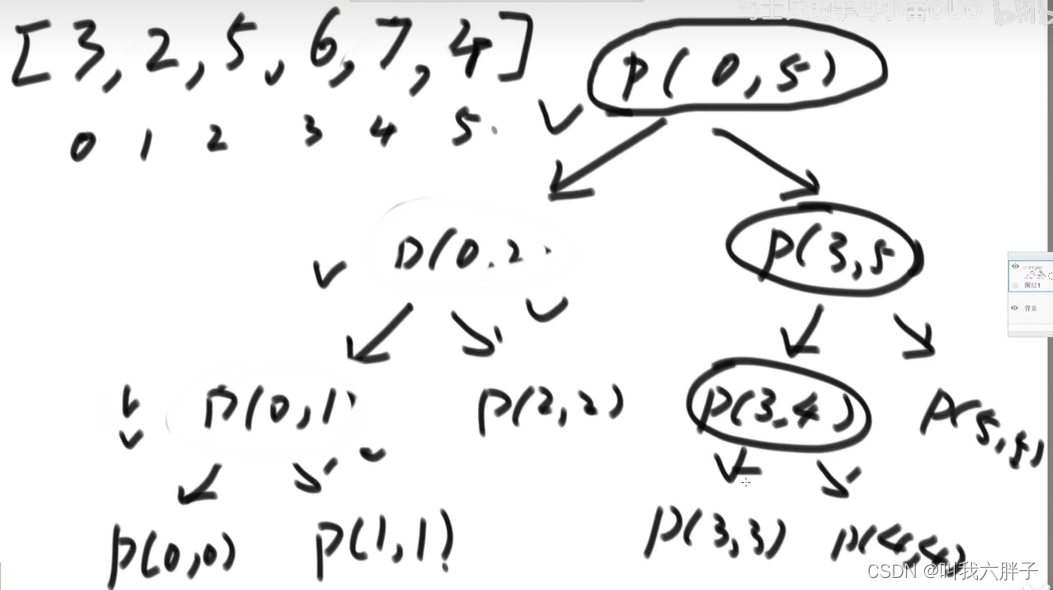
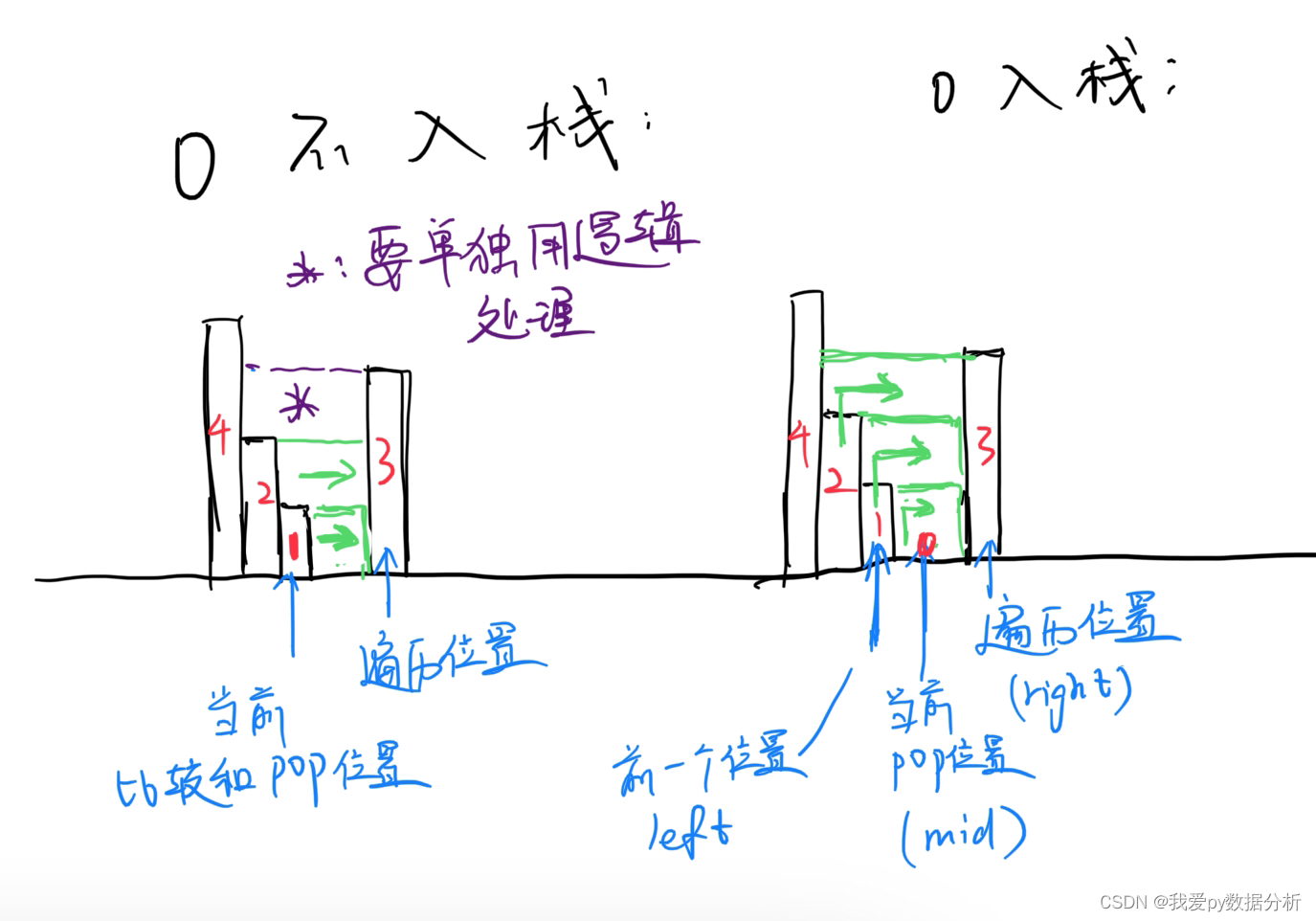
p(0,5)->p(0,2)->p(0,1)->p(0,0)-返回结果>p(0,1)->p(1,1)-返回结果>p(0,1)-返回结果,取消p(0,1)压栈>p(0,2)->p(2,2)-返回结果>p(0,2)-返回结果,取消p(0,2)压栈>p(0,5)->p(3,5)->p(3,4)->p(3,3)-返回结果>p(3,4)->p(4,4)-返回结果>p(3,4)-返回结果,取消p(3,4)压栈>p(3,5)->p(5,5)-返回结果>p(3,5)-返回结果,取消p(3,5)压栈>p(0,5)
1.7.2master公式
master公式
T(N)=a* T(N/b)+O(N^d)
log(b,a)>d -> 复杂度为 O(N^log(b,a))
log(b,a)=d -> 复杂度为 O(N^d *logN)
log(b,a)< d -> 复杂度为 O(N^d)
T(N)母问题的数据量是T(N)级别的有N个数据
T(N/b)子问题的规模
a为子问题调用次数
O(N^d)除去调用之外剩下的过程的时间复杂度
使用master公式 需要看子问题规模是不是等量的,等量才可以使用
三个值一旦确定即可找出时间复杂度
logba<d 的时间复杂度O(Nd)
logba>d 的时间复杂度O(N^logb a )
logba==d 的时间复杂度O(Nd * logN)