题目：

 

思路：

连通的部分加起来，然后总的 减去连通的部分。

但是很可惜 只能通过部分

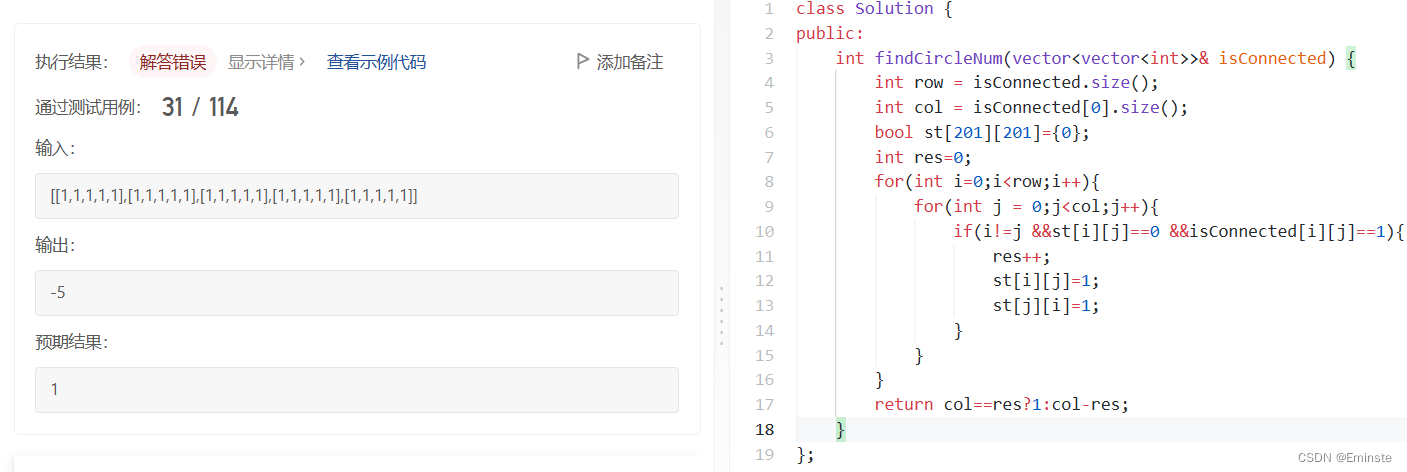
 似乎将st[i][j] st[j][i] 改变之后是可行的 但是实际上 1 2 连通后 2 1 确实是不会再加。 但是  2 3却还是在加一遍。

好吧。答案的思路是使用并查集。将连通的部分变为一个集合。然后数里面有几个集合。

 

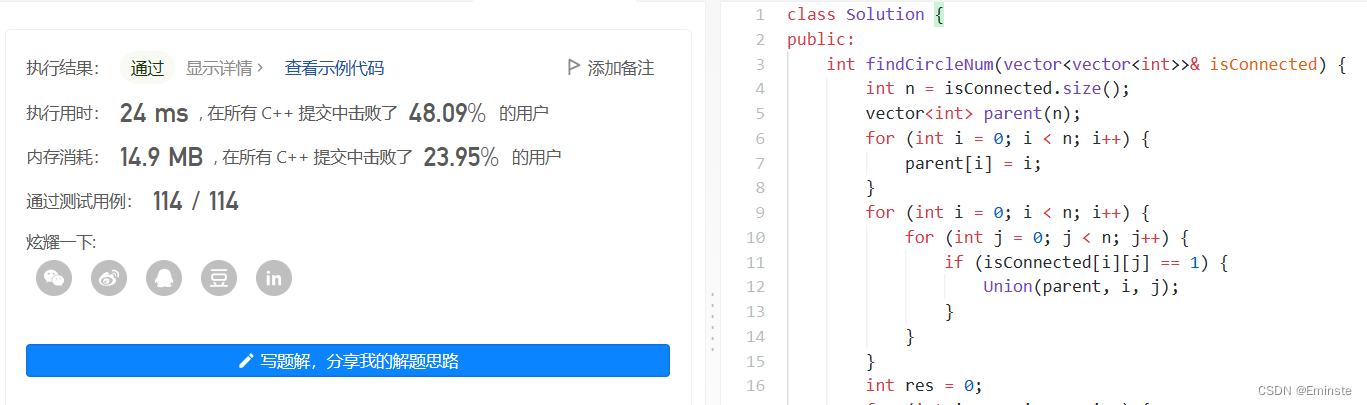
代码是：

//code
 
class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        int n = isConnected.size();
        vector<int> parent(n);
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (isConnected[i][j] == 1) {
                    Union(parent, i, j);
                }
            }
        }
        int res = 0;
        for (int i = 0; i < n; i++) {
            if (parent[i] == i) {
                res++;
            }
        }
        return res;
    }

private:
    int Find(vector<int>& parent, int i) {
        if (parent[i] == i) {
            return i;
        }
        parent[i] = Find(parent, parent[i]);
        return parent[i];
    }

    void Union(vector<int>& parent, int i, int j) {
        int pi = Find(parent, i);
        int pj = Find(parent, j);
        parent[pi] = pj;
    }
};

假设输入为：

[[1,1,0,0,0],
 [1,1,0,0,0],
 [0,0,1,1,0],
 [0,0,1,1,0],
 [0,0,0,0,1]]

运行过程如下：

1.  初始化parent数组为[0, 1, 2, 3, 4]，每个城市的父节点都是它自己。
2. 2遍历矩阵中的每一条边，当i=0,j=1时，发现城市0和城市1相连，将它们所在的集合合并，即将城市0的父节点设置为1，此时parent数组变为[1, 1, 2, 3, 4]；当i=1,j=0时，由于城市0已经和城市1相连，所以不需要再次合并它们所在的集合。
3.  继续遍历矩阵中的每一条边，当i=2,j=3时，发现城市2和城市3相连，将它们所在的集合合并，即将城市2的父节点设置为3，此时parent数组变为[1, 1, 3, 3, 4]；当i=3,j=2时，由于城市2已经和城市3相连，所以不需要再次合并它们所在的集合。
4. 继续遍历矩阵中的每一条边，当i=4,j=4时，发现城市4和城市4相连，因此不需要进行任何操作。
5. 最后，统计有多少个城市的父节点是它自己，发现有3个，因此省份的数量为3，返回结果。