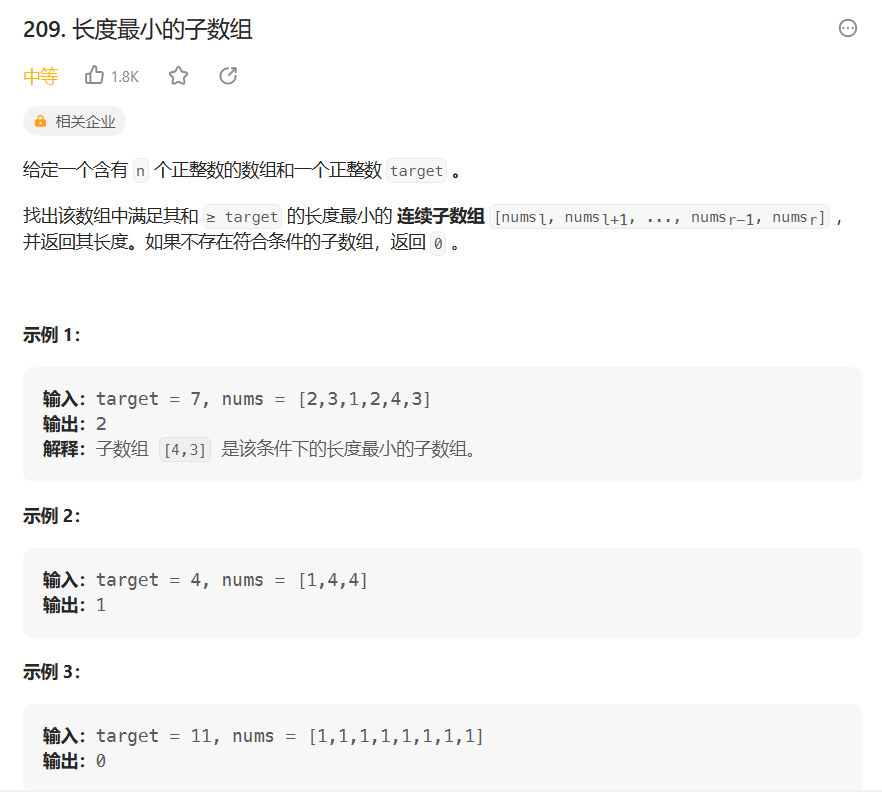
暴力破解：二次for循环遍历num[i]+...+num[j]，记录满足条件的最小长度

前缀和+二分：前缀和降低计算num[i]+...+num[j]的时间复杂度

                        对前缀和数组中的每个数进行遍历，找到距离这个数满足条件的最小长度

                        前缀和数组单调递增，此时查找可以使用二分查找

二分查找获取子数组 sum[0], sum[1], ..., sum[i] 上从右往左数第一个 sum[i] - sum[index] < target 的索引，那么sum[i] - sum[index-1] >= target，mid-1即为要找的索引位置，此时记录长度

i-(index-1)，将这个长度与之前存储的长度比较大小

 

为什么不找第一个sum[i]-sum[index]>=target的索引？

以第一个例子为例，前缀和数组在i=3时为sum:{2,5,6,8,0,0}，此时需要查找sum[i]-sum[index]>=target的索引，二分一直向前查找，没有找到，返回结果为最终的left=0，但是由于需要查找的数为大于等于的索引，此时记录的长度为i-index，导致记录的长度有误

总结：因为找sum[i]-sum[index]>=target不好找（好像废话）

代码

import org.junit.Test;

public class MinLengthSubarray {

    @Test
    public void test() {
        int target = 7, target1 = 4, target2 = 11;
        int[] nums = new int[]{2, 3, 1, 2, 4, 3};//2
        int[] nums1 = new int[]{1, 4, 4};//1
        int[] nums2 = new int[]{1, 1, 1, 1, 1, 1};//0
        System.out.println(minLengthSubarry(nums, target));
//        System.out.println(minLengthSubarry(nums1, target1));
//        System.out.println(minLengthSubarry(nums2, target2));
    }

    public static int minLengthSubarry(int[] nums, int target) {
        int res = Integer.MAX_VALUE;

        //创建前缀和数组
        int[] sum = new int[nums.length];
        sum[0] = nums[0];//给第一个数赋值，第一个数无法相加

        //sum[0]==nums[0]，只有一个数
        if (sum[0] >= target) {
            return 1;
        }

        for (int i = 1; i < nums.length; i++) {
            sum[i] = sum[i - 1] + nums[i];

            if (sum[i] > target) {//缩小查找范围，优化算法
                res = Math.min(res, i - lookForIndex1(sum, i, target) + 1);//找到最小长度
            }
        }
        return res == Integer.MAX_VALUE ? 0 : res;
    }

    //寻找第一个sum[i]-sum[mid]<target的索引
    //最终返回长度为i-(index-1)
    public static int lookForIndex1(int[] sum, int i, int target) {
        int left = 0, right = i;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (sum[i] - sum[mid] < target) {
                right = mid;//mid左移动，不减一因为mid可能是第一个sum[i]-sum[mid]<target的索引
            } else {//sum[i]-sum[mid] >= target
                left = mid + 1;//右移，因为要找第一个；加一因为mid不可能第一个sum[i]-sum[mid]<target的索引
            }
        }
        return left;
    }

}