写在前面的话：论文的证明和一些公式具有一定的跳跃性，而且可能我没有L1稀疏平滑相关的理论基础知识，导致这篇文章我看了很久，也只是看懂个大概，特别是lop关于二阶近似证明的后半部分。这篇论文是点云平滑中一个经典的算法，后续可能会根据源码再次理解论文细节。

lop

概要

在本文中，我们介绍了一种无参数化的局部投影算子（LOP:Optimal Projection operator）。它使用了更原始的投影机制，更稳健，并且在复杂场景中运行良好。此外，如果数据点是从光滑表面局部采样的，则算子提供二阶近似，从而得到采样表面的合理近似。新的投影算子是通过某个不动点迭代引入的，其中近似几何由其不动点组成。该方法的起源是 Weiszfeld 解决 Fermat-Weber 点位置问题的算法，也称为多元 L1 中值。这是一种统计工具，传统上全局应用于多元非参数点样本，以便在存在噪声和异常值的情况下为大量样本生成良好的代表。该问题最初被称为 Weber [1909] 的最优位置问题。任务是为工业场地找到一个最佳位置，最大限度地降低访问成本。在统计学中，这个问题被称为 L1 中位数 [Brown 1983；小1990]。 Weiszfeld [1937]提出了一个简单的迭代过程来计算 L1 中值。后来，Kuhn[1973]对Weiszfeld的算法进行了严格的处理，并指出这个问题可以追溯到17世纪初的费马。费马-韦伯（全局）点位置问题被视为空间中位数，因为如果仅限于单变量情况，它与单变量中位数一致，并且它在多变量设置中继承了它的几个属性。

lop定义

给定数据点集 P = {p j} j∈J，LOP 将任意点集 $X^{(0)}$ = {$x_i^{(0)}$ }i∈I投影到集合 P 上，其中 I, J表示索引集。我们通过最小化到 P 点的加权距离之和得到投影点集 Q = {qi}i∈I。此外，点Q不应彼此太靠近。该框架将所需点 Q 定义为方程（1）的不动点解：

$$Q=G(Q)\text{\hspace{1em}(1)}$$

G ( C ) = argmin ⁡ X = { x i } i ∈ I { E 1 ( X , P , C ) + E 2 ( X , C ) } , E 1 ( X , P , C ) = ∑ i ∈ I ∑ j ∈ J ∥ x i − p j ∥ θ ( ∥ c i − p j ∥ ) , E 2 ( X , C ) = ∑ i ′ ∈ I λ i ′ ∑ i ∈ I \ { i ′ } η ( ∥ x i ′ − c i ∥ ) θ ( ∥ c i ′ − c i ∥ ) . (2) \begin{aligned} & G(C)=\operatorname{argmin}_{X=\left\{x_i\right\}_{i \in I}}\left\{E_1(X, P, C)+E_2(X, C)\right\}, \\ & E_1(X, P, C)=\sum_{i \in I} \sum_{j \in J}\left\|x_i-p_j\right\| \boldsymbol{\theta}\left(\left\|c_i-p_j\right\|\right), \\ & E_2(X, C)=\sum_{i^{\prime} \in I} \lambda_{i^{\prime}} \sum_{i \in I \backslash\left\{i^{\prime}\right\}} \eta\left(\left\|x_{i^{\prime}}-c_i\right\|\right) \boldsymbol{\theta}\left(\left\|c_{i^{\prime}}-c_i\right\|\right) . \end{aligned}\tag{2} ​G(C)=argminX={xi​}i∈I​​{E1​(X,P,C)+E2​(X,C)},E1​(X,P,C)=i∈I∑​j∈J∑​∥xi​−pj​∥θ(∥ci​−pj​∥),E2​(X,C)=i′∈I∑​λi′​i∈I\{i′}∑​η(∥xi′​−ci​∥)θ(∥ci′​−ci​∥).​(2)

这里 θ ® 是一个快速递减的平滑权重函数，其支撑半径 h 定义了影响半径的大小，η® 是另一个惩罚 xi′ 的递减函数使得点之间不能靠的太近，而 {λi}i εI 是平衡项，我们用 Λ 表示。简而言之，E1 项驱动投影点 Q 逼近 P 的几何形状，而 E2 项则致力于保持点 Q 的分布均匀。
下面，我们逐一解释这两个术语，然后我们证明，假设数据是从 C2 表面采样的，适当的值 Λ 可以保证 LOP 算子的二阶逼近。
注解：根据下文的证明假设X=Q，因此把X和Q看成同一个变量即可。

L1 中位数:第一个代价函数 E1 与多元中位数（也称为 L1 中位数）密切相关。给定数据集 P，L1 中值定义为点 q，最小化到数据点的欧几里得距离之和：

$$q=\underset{x}{\mathrm{argmin}}\left\{\sum _{j\in J}\Vert p_j-x\Vert \right\}\text{\hspace{1em}(3)}$$

与平均值不同，“L1”中位数对数据中异常值的并不敏感。 E1 可以看作是 (3) 中代价函数的局部版本，其目的是从 P 中获得几何的局部近似值：我们不是寻找代表所有数据点 P 的一个点 q，而是寻找一组点 Q = {qi}i∈I 代表几何形状。我们使用具有有限支撑半径 h 的快速衰减权重函数 θ 来局部化代价函数（我们使用近似值 $\theta (r)=e^{-r^2/(h/4{)}^2}$）。等式

$$Q=\underset{X}{\mathrm{argmin}}{E}_1(X,P,Q)\text{\hspace{1em}(4)}$$

的解可以解释为集合 Q的局部分布中心.

正则化：(4) 的解对表面上的点产生了良好的近似，但所得点 Q 具有不规则的空间分布，并且倾向于聚集成簇。第二个代价函数 E2(X, Q) 通过结合局部排斥力来规范 Q 中的点。我们通常使用 η® = 1/3$r^3$ 形式的斥力函数。与涉及两个代价函数之和的其他最小化问题一样，为（2）中的参数 Λ 设置适当的值非常重要。小的 Λ 值可以实现良好的近似，但代价是分布较差。另一方面，较大的 Λ 值会赋予数据独立项以权重，该项力求点的均匀分布。正如我们接下来将要展示的，可以选择 Λ 来保证 LOP 具有 O(h2) 近似阶数，其中 h 是权重函数 θ 的支持大小。

lop的近似阶数:LOP 的近似阶数。 LOP 算子的一个重要特性是能够在没有任何局部方向信息或局部流形假设的情况下近似曲面。在LOP的应用中起主要作用的一个重要参数是h，即权重函数θ的支持大小。以下定理保证了当 h → 0 时渐近 lop具有O(h2) 近似阶数。作为近似阶数分析的额外成果，我们还应推导出计算 LOP 过程中平衡参数 Λ 的正确选择。

证明:In letting $h$ tend to zero we assume that the number of projected points, $I$, is fixed, while the number of input points, $J$, may grow. $G(C)$, as defined in (2), satisfies ${{\nabla }_X|}_{X=G(C)}\left(E_1(X,P,C)+E_2(X,C)\right)=0$. Therefore, the points Q = { q i } i ∈ I Q=\left\{q_i\right\}_{i \in I} Q={qi​}i∈I​ defined by Eq. (1) satisfying ${{\nabla }_X|}_{X=Q}\left(E_1(X,P,Q)+E_2(X,Q)\right)=0$, which leads to the relation:

∑ j ∈ J ( q i ′ − p j ) α j i ′ − λ i ′ ∑ i ∈ I \ { i ′ } ( q i ′ − q i ) β i i ′ = 0 , i ′ ∈ I , (5) \sum_{j \in J}\left(q_{i^{\prime}}-p_j\right) \alpha_j^{i^{\prime}}-\lambda_{i^{\prime}} \sum_{i \in I \backslash\left\{i^{\prime}\right\}}\left(q_{i^{\prime}}-q_i\right) \beta_i^{i^{\prime}}=0, \quad i^{\prime} \in I,\tag{5} j∈J∑​(qi′​−pj​)αji′​−λi′​i∈I\{i′}∑​(qi′​−qi​)βii′​=0,i′∈I,(5)
where ${\alpha }_j^{i^{\prime }}=\frac{\theta \left(\Vert q_{i^{\prime }}-p_j\Vert \right)}{\Vert q_{i^{\prime }}-p_j\Vert },j\in J$ and ${\beta }_i^{i^{\prime }}=\frac{\theta \left(\Vert q_{i^{\prime }}-q_i\Vert \right)}{\Vert q_{i^{\prime }}-q_i\Vert }\left|\frac{\partial \eta \left(\Vert q_{i^{\prime }}-q_i\Vert \right)}{\partial r}\right|$, i ∈ I \ { i ′ } i \in I \backslash\left\{i^{\prime}\right\} i∈I\{i′}. Note that we have used the fact that $\eta$ is decreasing, that is, its derivative is always negative. After rearranging and setting ${\lambda }_{i^{\prime }}=\mu \frac{{\sum }_{j\in J}{\alpha }_j^{i^{\prime }}}{{\sum }_{i\in I\backslash i^{\prime }\}}{\beta }_i^{i^{\prime }}},\mu >0$, we get
( 1 − μ ) q i ′ + μ ∑ i ∈ I \ { i ′ } q i β i i ′ ∑ i ∈ I \ { i ′ } β i i ′ = ∑ j ∈ J p j α j i ′ ∑ j ∈ J α j i ′ , i ′ ∈ I . (6) (1-\mu) q_{i^{\prime}}+\mu \sum_{i \in I \backslash\left\{i^{\prime}\right\}} q_i \frac{\beta_i^{i^{\prime}}}{\sum_{i \in I \backslash\left\{i^{\prime}\right\}} \beta_i^{i^{\prime}}}=\sum_{j \in J} p_j \frac{\alpha_j^{i^{\prime}}}{\sum_{j \in J} \alpha_j^{i^{\prime}}}, \quad i^{\prime} \in I .\tag{6} (1−μ)qi′​+μi∈I\{i′}∑​qi​∑i∈I\{i′}​βii′​βii′​​=j∈J∑​pj​∑j∈J​αji′​αji′​​,i′∈I.(6)
Viewing (6) as a system of equations for $Q$,
$$AQ=R\text{\hspace{1em}(7)}$$
请注意，A 和 R 也取决于 Q，然而，通过分析 $A^{-1}$ 和 R，我们在下面显示 $Q=A^{-1}R$ 是距表面 S 距离 O(h2) 的点。证明了每个qi’ 是表面上或附近点的平均值。我们将使用这样的观察：平面上的点的affine average也在该平面上，并且该表面可以用平面局部近似，近似误差为 O(h2)。证明略。

不动点迭代lop算法

The above leads to an iterative solution to (1) which guarantees an $O\left(h^2\right)$ approximation order: Fix a repulsion parameter $\mu \in [0,1/2)$. Next, define $X^{(1)}={\left\{x_i^{(1)}\right\}}_{i\in I}$ by
$$x_{i^{\prime }}^{(1)}=\frac{{\sum }_{j\in J}{p}_j\theta \left(\Vert p_j-x_{i^{\prime }}^{(0)}\Vert \right)}{{\sum }_{j\in J}\theta \left(\Vert p_j-x_{i^{\prime }}^{(0)}\Vert \right)},i^{\prime }\in I.$$
Then, at each iteration $k=1,2,3,\dots$ define for $i^{\prime }\in I$
$${\alpha }_j^{i^{\prime }}=\frac{\theta \left(\Vert x_{i^{\prime }}^{(k)}-p_j\Vert \right)}{\Vert x_{i^{\prime }}^{(k)}-p_j\Vert },{\beta }_i^{i^{\prime }}=\frac{\theta \left(\Vert x_{i^{\prime }}^{(k)}-x_i^{(k)}\Vert \right)}{\Vert x_{i^{\prime }}^{(k)}-x_i^{(k)}\Vert }\left|\frac{\partial \eta }{\partial r}\left(\Vert x_{i^{\prime }}^{(k)}-x_i^{(k)}\Vert \right)\right|$$
for i ∈ I \ { i ′ } i \in I \backslash\left\{i^{\prime}\right\} i∈I\{i′}. Then, by rearranging (6) we derive our fixed point iterations as
x i ′ ( k + 1 ) = ∑ j ∈ J p j α j i ′ ∑ j ∈ J α j i ′ + μ ∑ i ∈ I \ { i ′ } ( x i ′ ( k ) − x i ( k ) ) β i i ′ ∑ i ∈ I \ { i ′ } β i i ′ , x_{i^{\prime}}^{(k+1)}=\sum_{j \in J} p_j \frac{\alpha_j^{i^{\prime}}}{\sum_{j \in J} \alpha_j^{i^{\prime}}}+\mu \sum_{i \in I \backslash\left\{i^{\prime}\right\}}\left(x_{i^{\prime}}^{(k)}-x_i^{(k)}\right) \frac{\beta_i^{i^{\prime}}}{\sum_{i \in I \backslash\left\{i^{\prime}\right\}} \beta_i^{i^{\prime}}}, xi′(k+1)​=j∈J∑​pj​∑j∈J​αji′​αji′​​+μi∈I\{i′}∑​(xi′(k)​−xi(k)​)∑i∈I\{i′}​βii′​βii′​​,
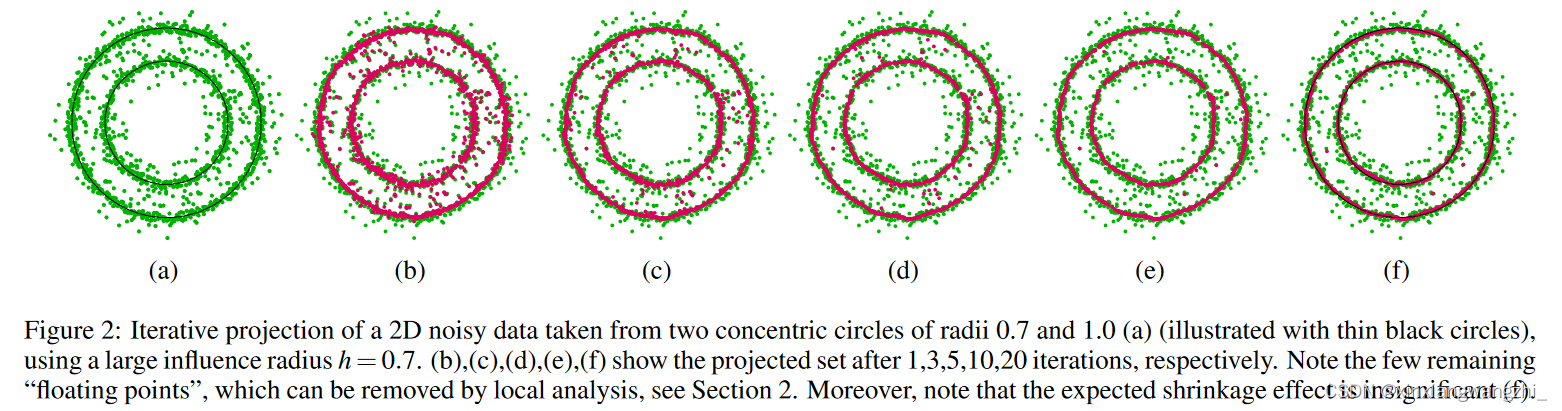
对于每个 i′ ∈ I。收敛时，极限满足必要条件（5），并且由定理 2.1 保证了近似阶数。图 2 显示了迭代过程。 有两种典型场景LOP 运算符可能无法按预期投影少数点：（i）点到表面的距离大于影响权重函数θ的支撑半径。 (ii) 该点恰好位于两个attractors的中间；例如，见图2(f)。

lop应用

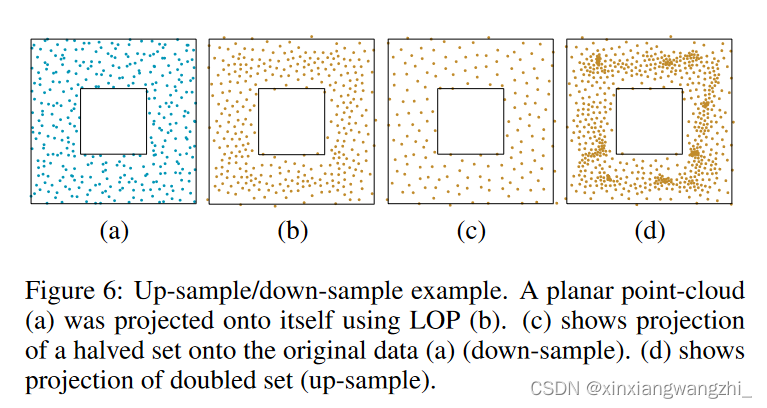
LOP 可用于将任意一组点 X(0) 投影到输入点云 P 上。我们观察到，采用少于 P 的点的 X(0) 会导致投影点的分布更加规则，见图 6 。基本原理是输入数据可以被视为由相同数据的多次观察组成，并且 LOP 能够很好地表示输入数据的简洁点集。从某种意义上说，它的运作就像多元中位数，它定义了一组样本的代表。

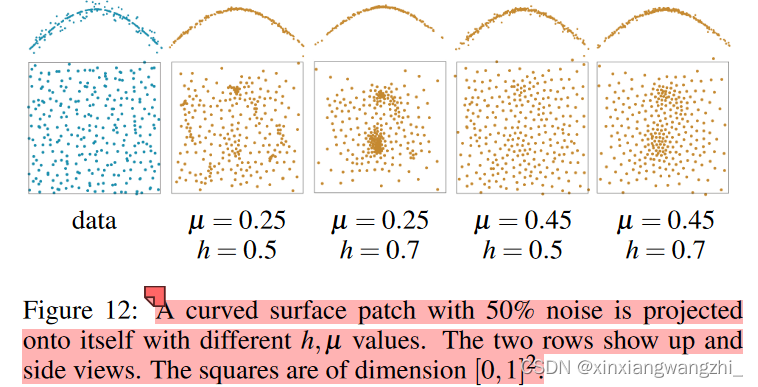
LOP算法由两个参数控制：h和μ。研究它们对投影集Q的性质的影响，见图12。h是算子的局部影响大小；通常最好以与预期异常值大小一样大的 h 开始迭代，然后随着迭代的进行而优化 h。类似地，可以从较小的μ开始，然后增加它。

lop算法实验结果

该算法通常需要 20 次平均迭代才能将点集投影到自身上。如果初始猜测 X(0) 非常粗略，并且该算法需要数百次迭代。
与mls对比的结果：比mls效果好很多

wlop

LOP 通常效果很好，但我们发现，当 r 较大时，正则化函数 η® = 1/3$r^3$ 可能下降得太快而无法保证足够的惩罚。这可能导致缺乏明确的收敛和不均匀的点分布。为此，我们建议使用新的斥力 η®=−r，它的减小更加平缓，并且在 r 较大时惩罚更多，从而产生更好的收敛性和更均匀的点分布。

LOP 优化标准中的第一项与多元中位数密切相关，也称为L1中位数，它导致投影点向局部分布中心移动。如果给定的点云不均匀，无论我们选择什么初始集X0，LOP的投影都倾向于遵循这种不均匀的趋势。在某些情况下，这可能是理想的，例如，允许形状特征附近有更高的点密度。在其他情况下，人们可能更喜欢各处的均匀点分布。为了点云分布的更加均匀，我们建议将局部自适应密度权重合并到LOP中，从而产生 WLOP。
让我们定义第 k 次迭代期间 P 中的每个点 pj 和 X 中的 xi 的加权局部密度： v j = 1 + ∑ j ′ ∈ J \ { j } θ ( ∥ p j − v_j=1+\sum_{j^{\prime} \in J \backslash\{j\}} \theta\left(\| p_j-\right. vj​=1+∑j′∈J\{j}​θ(∥pj​− $p_{j^{\prime }}\Vert )$ and w i k = 1 + ∑ i ′ ∈ I \ { i } θ ( ∥ δ i i ′ k ∥ ) , k = 0 , 1 , 2 … w_i^k=1+\sum_{i^{\prime} \in I \backslash\{i\}} \theta\left(\left\|\delta_{i i^{\prime}}^k\right\|\right), k=0,1,2 \ldots wik​=1+∑i′∈I\{i}​θ( ​δii′k​ ​),k=0,1,2… Then the projection for point $x_i^{k+1}$ finally becomes
x i k + 1 = ∑ j ∈ J p j α i j k / v j ∑ j ∈ J ( α i j k / v j ) + μ ∑ i ′ ∈ I \ { i } δ i i ′ k w i ′ k β i i ′ k ∑ i ′ ∈ I \ { i } ( w i ′ k β i i ′ k ) , x_i^{k+1}=\sum_{j \in J} p_j \frac{\alpha_{i j}^k / v_j}{\sum_{j \in J}\left(\alpha_{i j}^k / v_j\right)}+\mu \sum_{i^{\prime} \in I \backslash\{i\}} \delta_{i i^{\prime}}^k \frac{w_{i^{\prime}}^k \beta_{i i^{\prime}}^k}{\sum_{i^{\prime} \in I \backslash\{i\}}\left(w_{i^{\prime}}^k \beta_{i i^{\prime}}^k\right)}, xik+1​=j∈J∑​pj​∑j∈J​(αijk​/vj​)αijk​/vj​​+μi′∈I\{i}∑​δii′k​∑i′∈I\{i}​(wi′k​βii′k​)wi′k​βii′k​​,
where ${\alpha }_{ij}^k=\frac{\theta \left(\Vert {\xi }_{ij}^k\Vert \right)}{\Vert {\xi }_{ij}^k\Vert }$ and ${\beta }_{i{i}^{\prime }}^k=\frac{\theta \left(\Vert {\delta }_{i{i}^{\prime }}^k\Vert \right)|{\eta }^{\prime }\left(\Vert {\delta }_{i{i}^{\prime }}^k\Vert \right)|}{\Vert {\delta }_{i{i}^{\prime }}^k\Vert }$. 因此，给定集合 P 中点簇的吸引力通过第一项中的加权局部密度 v 得到缓解，而来自密集区域中的点的排斥力通过第二项中的加权局部密度 w 得到加强。请注意，通过将所有密度权重设置为 1，具有新斥力项的 LOP 是 WLOP 的特殊情况。在这种情况下，可以显示假设解附近的定点迭代的收缩。
参考文献：
《Parameterization-free Projection for Geometry Reconstruction》
《Consolidation of Unorganized Point Clouds for Surface Reconstruction》
不动点迭代