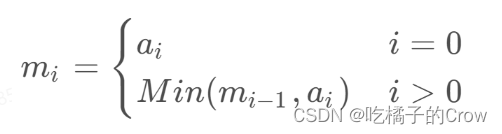针对极端学生化偏差(Extreme Studentized Deviate,ESD)算法只能对单变量数据进行异常检测,难以对多变量数据进行异常行为度量,提出一种复杂微服务系统异常行为分析与定位(Multivariate Seasonal Hybrid ESD,M.S-H-ESD)算法。首先,对云平台的微服务运维日志数据进行提取,将多元日志数据进行加权归一得到一元数据。然后,对此一元数据采用多元周期混合ESD(Seasonal Hybrid ESD,S-H-ESD)算法对每个服务的异常度进行度量,进而获得异常度最高的服务,根据置信度和异常上限的设置,定位微服务系统异常的根因服务。实验结果表明,M.S-H-ESD算法对时间序列多维数据的异常行为检测具有较高的精确度、召回率和F1值,能够准确定位微服
务系统中的异常服务。
目录
1 M.S - H - ESD 算法
1.1 数据处理
1.2 异常行为分析与定位
1 M.S - H - ESD 算法
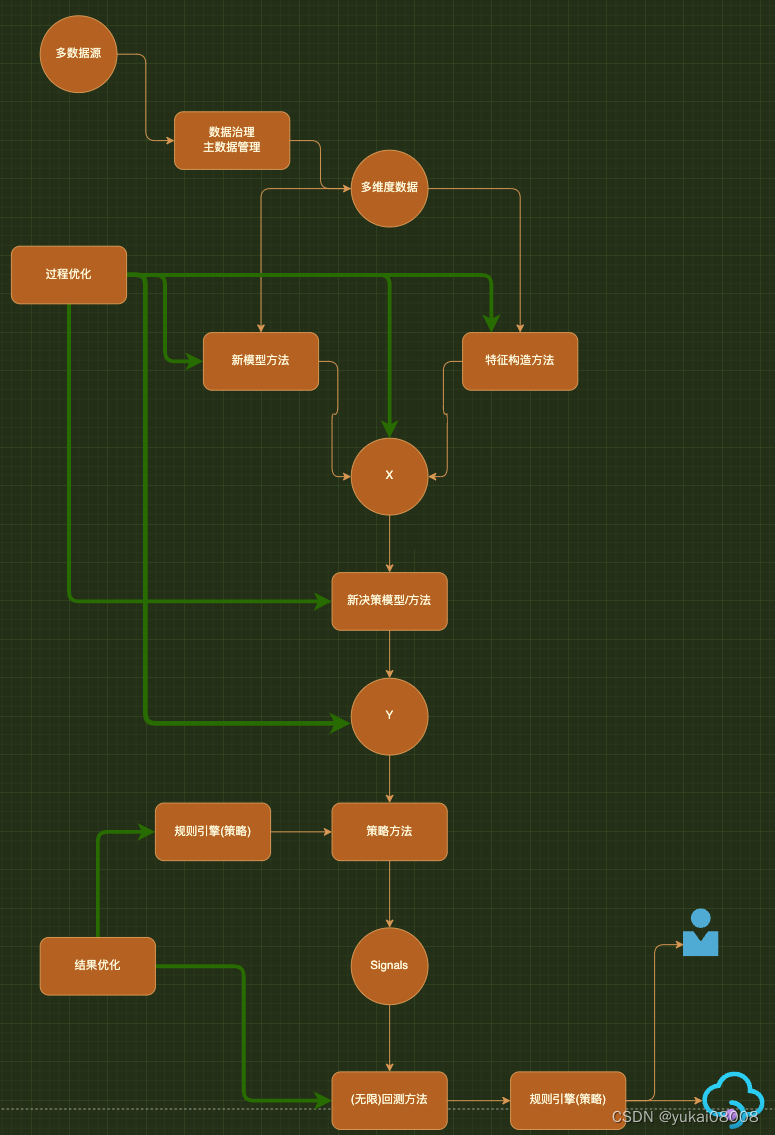
基于多元微服务日志的根因服务异常分析方法主要包含多元数据处理、模型训练和异常评分、模型评估以及故障修复等4个部分,具体过程示意图如图1所示。
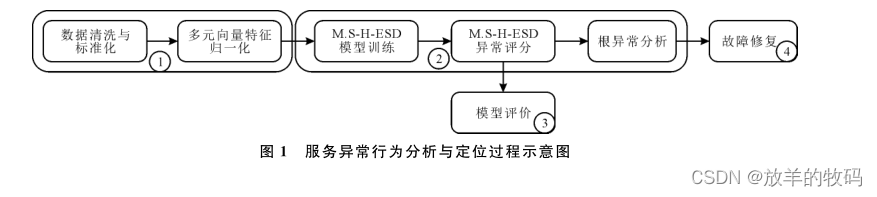
1 )多元数据处理。基于微服务系统的半结构化日志,通过正则表达式或自动抽取工具抽取相关的重要信息,将半结构化的日志信息转变为结构化的数据。对结构化数据清洗和标准化后,提取多元数据的特征值和特征根,求出每一维度数据的贡献度,对多元数据进行加权归一处理。
2 )模型训练和异常评分。对获取的服务数据按调用方式分组,对每组服务使用 M.S - H -
ESD算法计算每个服务为其他服务调用的服务评分。根据设置的阈值得到根服务的异常和定位结果,其中异常得分的上限越高,得到的异常根因服务越紧致,反之得到的异常根因服务越松弛。最后,按照得分结果进行排序,最有可能发生异常的根因服务就 在其 中,排 序 愈 靠 前,发 生 异 常 的 可 能 性越大。
3 )模型评价。常用的评价指标有准确率、查全率和 F1 值。准确性是最常见的评价指标,精确度越高,分类器越好,在对非均衡分布数据集的召回率和 F1 值的应用中,其是更客观地反映分类器在评价方面的指标。
4 )故障修复。根据根因服务的异常分析结果进行故障修复,故障修复包括人工修复或系统自愈。
1.1 数据处理
对多元微服务日志数据某一实体属性的研究涉及 p 个指标,分别用 x 1 , x 2 ,…, xp 表示,则 p 个指标组成的 p 维随机向量 x = ( x 1 , x 2 ,…, xp )T 。设随机向量 x 的均值为 μ ,协方差矩阵为 Ψ 。 x 的线性变换可以形成一个新的合成变量 y ,即新的合成变量 y 可以用原变量线性表示为:

算法步骤如下:
步骤1:读取输入,并对输入数据采用 minmax方法标准化,将初步处理后的数据记为 D 。
步骤2:利用主成分分析 [30 ] (Principal Compo -nents Analysis , PCA )模型得到 D 的协方差矩阵 Ψ的特征向量 X 、特征值 θ 和方差贡献率 υ 。
步骤3:计算成分得分系数矩阵 K 。
步骤4:计算 D 中每个属性的权重。
步骤5:返回每一条记录的加权归一化数据。
步骤6:根据原始数据调用服务和被调服务对一元数据 F i 进行分组。
1.2 异常行为分析与定位
利用 ESD 算法获取一元数据的异常点,具体步骤如下:
步骤1:计算均值的数据序列应先删除上一轮最大残差样本数据,均值偏离最远残差的表达式为:
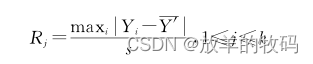
步骤2: 计算临界值:
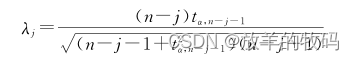
式中:n 为数据集的样本数; α 为置信度。
步骤3: 对比均值偏离最远残差与临界值大小,若 R i > λj ,则原假设 H 0 不成立,该样本点为异常点。
步骤4:重复以上步骤 k 次至算法结束。
ESD算法在处理原始数据的时候,并未考虑微服务日志数据本身具有时间序列的特征,为了更好地提取特征,在原有一元数据的基础上,对数据进行去周期和趋势。
基于 Loess的周期趋势分解( Seasonal- TrendDecompositionProcedure based on Loess , STL )将时间序列数据分解为趋势分量、周期分量和余项分量。将ESD 算法运用于 STL 分解后的余项分量中,即可得到时间序列上的异常点,但在余项分量中存在着部分假异常点。为了解决这种假阳性降低准确率的问题,采用中位数( median )替换趋势分量。设原时间序列数据为 T , STL分解后的周期分量 S T ,则残差余项分量的计算表达式为:

考虑到个别异常值会极大地拉伸均值和方差,导致式中的余项分量计算未能很好地捕获到部分异常点,召回率偏低。绝对中位差的计算表达式为:
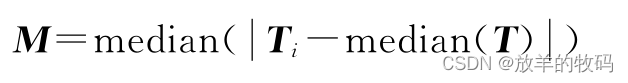
以上两式子代入后:

设某调用服务 i 发生的异常数为 a ,被调用服务发生的异常数为 b ,调用服务异常得分为:
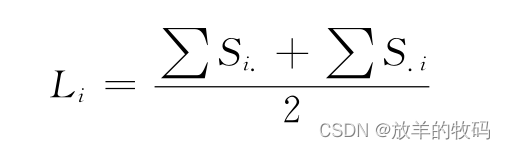
由调用服务异常得分 L i 得到调用服务加权异常得分的表达式为:

M.S - H - ESD算法具体步骤如下:
步骤1: 读取结构化日志数据。
步骤2: 利用对读取数据进行加权并归一化得到一元数据。
步骤3: 根据调用服务和被调服务对一元数据进行分组提取。
步骤4: 将每条数据利用计算均值偏离最远残差 R j 和临界值 λj 。若 R j > λ j ,则 H 0原假设不为真,采样点为异常点。调整置信度 α 和异常得分的上限 u ,会得到不同服务下异常得分的值。记录该所有采样点,即分组的调用服务和被调服务的异常得分矩阵 S 。
步骤5: 根据调用服务和被调用服务矩阵的异常得分 S ,加权得到每个服务的异常度得分 G i 。
步骤6: 对微服务的异常度得分 G 进行排序,即为获取根本原因异常服务,且异常可能性顺序递减。