概念
枚举:就是把满足题目条件的所有情况都列举出来,然后一一判断寻找最优解的过程
1.最值问题
1.两个数的最值问题
两个数的最小值,利用Java的运算符就可以实现
int Min(int a,int b){
return a<b?a:b;
}2.n个数的最值问题
当有n个数时Ai时,我们可以首先取前两个数,计算最小值;然后再拿这个最小值和第三个数去比较,得到的最小值再去和第四个数进行比较,一次类推,就可以计算出n个数中最小的值
假设前i个数的最小值为min,则有递推公式如下:
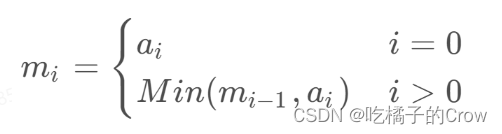
所以将这个递推公式翻译成java代码是这样的:
public int min(int a,int b){
return a<b?a:b;
}
public int findMin(int[] num){
int min=num[0];
for(int i=1;i<num.length;i++){
min=min(min,num[i]);
}
return min;
}3.最值问题的下标
有些时候我们求的并不是一个最小的数,而是要求出这个数组中最小数的下标,那么可以直接记录下标,并且比较的时候直接通过下标去索引到值,然后再进行比较,像这样:
public int findMin(int[] num){
int minIndex=0;
for(int i=1;i<num.length;i++){
if(num[i]<num[minIndex]){
minIndex=i;
}
}
return minIndex;
}2.最值问题的进阶
1.第三大的数
有时候,我们求最大的数不够,想要求次大的,或者是第三大的数,我们应该怎么做呢?这样的问题,核心思路就是先把最大的求出来,然后忽略最大数的情况下,再去求最大的,这时候就得到次大的了,再把次大的忽略掉,再次求最大的,就是第三大值了
2.数组中两元素的最大乘积
要求找到数组中两个元素的最大乘积,数组元素一定是正数,那么我们知道最大的元素相乘一定是最大的,所以就是找到最大值和次大值,但是这个问题和第三大的数稍微有点区别,相同的数会被计算进去,所以我们找到最大值以后,可以将它的下标忽略掉,然后再去找最大的值,这样找到的一定是两个可重复的最大元素和次大元素,将两者相乘即可。
3.降维思想
一些统计类问题,第一个思路就是枚举所有的情况,然后再次考虑是不是能够某些O(n)降为O(1),这就是降维思想,具体看
统计上升四元组的数目
1.O(n^4):
最坏的时间复杂度就是枚举i、j、k、l四个变量,然后判定nums四个数的关系,进行统计累加,但是这种做法在范围很大的时候势必超时
2.O(n^2)
- 首先,我们枚举j和k,然后对所有满足nums[i]>nums[j]的下标对,执行下一步
- 那么只要我们找到数组下标为0~j-1的数中,小于nums[k]的个数,记作a(也就是所有满足条件的i);找到数组下标为k+1~n-1的数中,大于nums[j]的个数,记作b(也就是所有满足条件的);将a*b就是所有满足条件的(i,l)对,把所有的(i,l)累加,就是我们要求出的答案
- 问题就转换为找到数组下标0~i-1的数中,小于nums[k]的个数和找到数组下标为k+1~n-1的数中,大于nums[i]的个数
Leetcode题单:
K个元素的最大和
class Solution {
public int maximizeSum(int[] nums, int k) {
if(nums==null||nums.length==0){
return 0;
}
int ans=0;
//执行k次循环
while(k!=0){
//保存最大值的下标
int maxIndex=0;
for(int i=0;i<nums.length;i++){
if(nums[i]>nums[maxIndex]){
maxIndex=i;
}
}
ans+=nums[maxIndex];
nums[maxIndex]+=1;
k--;
}
return ans;
}
}第三大的数
class Solution {
public int thirdMax(int[] nums) {
if(nums==null||nums.length==0){
return -1;
}
int[] s=Arrays.stream(nums).distinct().sorted().toArray();
if(s.length<3){
return s[s.length-1];
}
return s[s.length-3];
}
}统计上升四元组
class Solution {
public long countQuadruplets(int[] nums) {
// 初始化四元组的数量
long quadruplets = 0;
// 数组的长度
int n = nums.length;
// 记录每个数字的后面比它小的数字的个数
int[][] lessCount = new int[n][n + 1];
// 记录每个数字的前面比它大的数字的个数
int[][] greaterCount = new int[n][n + 1];
// 计算lessCount数组
getLess(nums, n, lessCount);
// 计算greaterCount数组
getGreater(nums, n, greaterCount);
// 遍历数组,计算满足条件的四元组数量
for (int j = 1; j < n - 2; ++j) {
for (int k = j + 1; k < n - 1; ++k) {
if (nums[k] < nums[j]) {
// 更新四元组数目
quadruplets += (long) (lessCount[j - 1][nums[k]] * greaterCount[k + 1][nums[j]]);
}
}
}
// 返回结果
return quadruplets;
}
// 计算lessCount数组
void getLess(int[] nums, int n, int[][] lessCount) {
// 遍历数组,计算每个数字的后面比它小的数字的个数
for (int i = 0; i < n; ++i) {
if (i != 0) {
// 复制上一行的数组值
lessCount[i] = Arrays.copyOf(lessCount[i - 1], n + 1);
}
// 统计后面比当前数字小的数字的个数
for (int j = nums[i]; j < n; ++j) {
++lessCount[i][j];
}
}
}
// 计算greaterCount数组
void getGreater(int[] nums, int n, int[][] greaterCount) {
// 遍历数组,计算每个数字的前面比它大的数字的个数
for (int i = n - 1; i >= 0; --i) {
if (i != n - 1) {
// 复制下一行的数组值
greaterCount[i] = Arrays.copyOf(greaterCount[i + 1], n + 1);
}
// 统计前面比当前数字大的数字的个数
for (int j = 1; j < nums[i]; ++j) {
++greaterCount[i][j];
}
}
}
}
/*
在给定的Java代码中,我们使用两个二维数组 lessCount 和 greaterCount 分别记录每个数字的后面比它小的数字的个数和前面比它大的数字的个数。
在 getLess 方法中,我们遍历数组 nums,对于每个数字 nums[i],我们复制上一行的数组值到当前行(即 lessCount[i] = Arrays.copyOf(lessCount[i - 1], n + 1))。然后,我们统计后面比当前数字小的数字的个数,即从 nums[i] 到 n-1,并将对应位置的计数器加1(++lessCount[i][j])。
在 getGreater 方法中,我们逆向遍历数组 nums,对于每个数字 nums[i],我们复制下一行的数组值到当前行(即 greaterCount[i] = Arrays.copyOf(greaterCount[i + 1], n + 1))。然后,我们统计前面比当前数字大的数字的个数,即从 1 到 nums[i] - 1,并将对应位置的计数器加1(++greaterCount[i][j])。
接下来,在 countQuadruplets 方法中,我们遍历 nums 数组的中间两个数字,即 j 和 k。我们检查 nums[k] 是否小于 nums[j],如果是,意味着满足题目要求的四元组 (nums[i], nums[j], nums[k], nums[l])。此时,我们可以利用之前计算的 lessCount 和 greaterCount 数组来获取符合条件的数量,即 lessCount[j - 1][nums[k]] 表示在 nums[j - 1] 之前比 nums[k] 小的数字的个数,而 greaterCount[k + 1][nums[j]] 表示在 nums[k + 1] 之后比 nums[j] 大的数字的个数。我们将这两个值相乘,并将其加到 quadruplets 中。
最后,我们返回 quadruplets,即满足题目要求的四元组的总数。
*/