图像增强

图像增强的方法是通过一定手段对原图像附加一些信息或变换数据，有选择地突出图像中感兴趣的特征或者抑制(掩盖)图像中某些不需要的特征，使图像与视觉响应特性相匹配。

图像对比度

图像对比度计算方式如下：
$$C=\sum _{\delta }\delta (i,j)P_{\delta }(i,j)$$
其中，$\delta (i,j)=|i-j|$，即相邻像素间的灰度差；$P_{\delta }(i,j)$为相邻像素灰度差为$\delta$的像素分布概率。可以是四邻域，也可以是八邻域。具体过程如下：
原始图像为：
$$L=\left[\begin{array}{ccc}1& 3& 5\\ 2& 1& 3\\ 3& 6& 0\end{array}\right]$$
按照四邻域进行计算，对比度$C_L=[(1^2+2^2)+(2^2+2^2+2^2)+(1^2+1^2+1^2)+(2^2+2^2+1^2+5^2)+(2^2+2^2+3^2)+(1^2+3^2)+(5^2+3^2+6^2)+(3^2+6^2)/22$。22就是平方的个数。

1.对比度展宽

对比度展宽的目的是通过增强图像的亮暗对比程度而改善画质，使图像的显示效果更加清晰。

线性对比度展宽

通过抑制非重要信息的对比度来腾出空间给重要信息进行对比度的展宽。

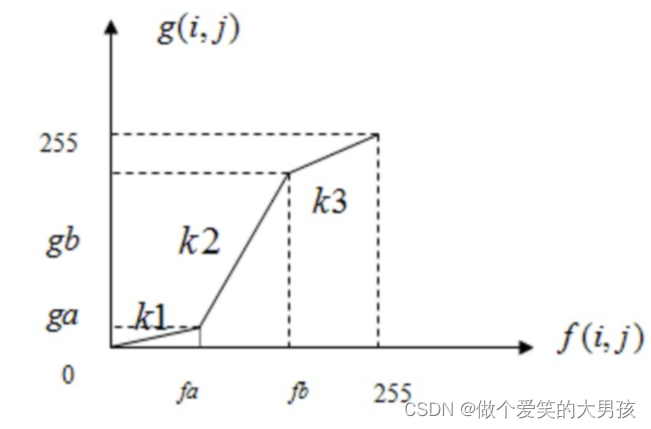
原图的灰度为$f(i,j)$，处理后的图像灰度为$g(i,j)$。原图中的重要景物的灰度分布假设分布在$[f_a,f_b]$的范围内，则对比度线性展宽的目的是使处理后图像的重要景物的灰度分布在$[g_a,g_b]$的范围内，当$\Delta f=(f_b-f_a)<\Delta g=(g_b-g_a)$，则可达到对比度展宽的目的。
计算方式如下：
$$g(i,j)=\{\begin{array}{ll}\alpha f(i,j)& 0\le f(i,j)<a\\ \beta (f(i,j)-a)+g_a& a\le f(i,j)<b\\ \gamma (f(i,j)-b)+g_b& b\le f(i,j)<255\end{array}$$
其中，$\alpha =\frac{g_a}{f_a},\beta =\frac{g_b-g_a}{f_b-f_a},\gamma =\frac{255-g_b}{255-f_b}$。
C++代码如下：

    cv::Mat image = cv::imread("Lena.bmp");
    cv::Mat grayImage(image.size(), CV_8UC1);
    cv::Mat dstImage(grayImage.size(), CV_8UC1);
    cv::cvtColor(image, grayImage, CV_BGR2GRAY);
    int fa = 50, fb = 100;
    float ga = 30, gb = 120;
    for (int row = 0; row < grayImage.rows; row++)
    {
        uchar *currentData = grayImage.ptr<uchar>(row);
        for (int col = 0; col < grayImage.cols; col++)
        {
            if (*(currentData + col) >= 0 && *(currentData + col) < fa)
            {
                dstImage.at<uchar>(row, col) = uchar(ga / fa * (*(currentData + col)));
            }
            if (*(currentData + col) >= fa && *(currentData + col) < fb)
            {
                dstImage.at<uchar>(row, col) = uchar((gb-ga) / (fb-fa) * (*(currentData + col)-fa)+ga);
            }
            if (*(currentData + col) >= fb && *(currentData + col) < 255)
            {
                dstImage.at<uchar>(row, col) = uchar((255-gb) / (255-fb) * (*(currentData + col)-fb)+gb);
            }
        }
        //currentData++;
    }

结果如下：

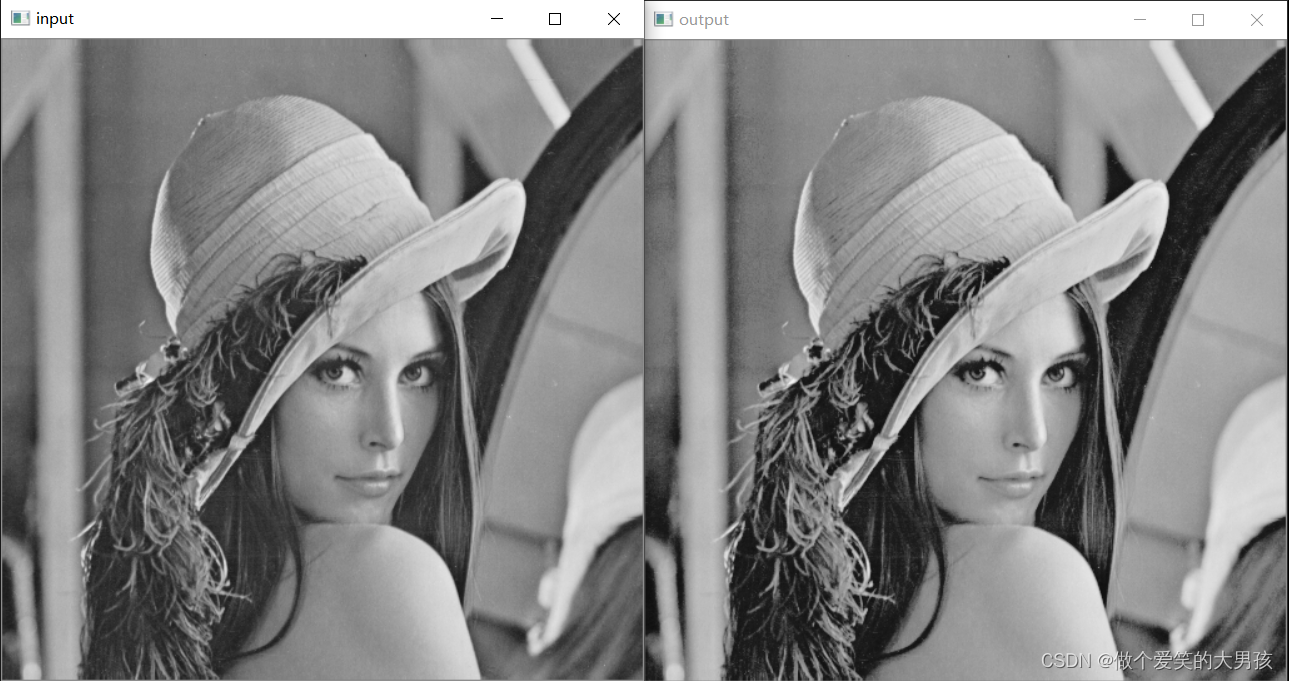
非线性对比度展宽

通过一个光滑的映射曲线，使得处理后图像的灰度变化比较光滑。计算公式如下：
$$g(i,j)=c\cdot lg(1+f(i,j))$$
实际上完成的作用是，抑制高亮度区域，扩展低亮度区域。

2.直方图均衡化

在信息论中有这样一个结论：当数据的分布接近均匀分布的时候，数据所承载的信息量（熵）为最大。
灰度直方图的基本原理是：对在图像中像素个数多的灰度级（即对画面起主要作用的灰度值）进行展宽，而对像素个数少的灰度值（即对画面不起主要作用的灰度值）进行归并。
直方图均衡化方法的具体步骤如下：

1. 求出原图$f(i,j{)}_{M\times N}$的灰度直方图，设用256维的向量$h_f$表示；
2. 有$h_f$求原图的灰度分布概率，记作$p_f$，则有$$p_f(i)=\frac{1}{N_f}\cdot h_f(i),i=0,1,\dots ,255$$
   其中，$N_f=M\times N$（$M,N$分别为图像的长和宽）为图像的总像素个数；
3. 计算图像各个灰度值的累计分布概率，记作$p_a$，则有$$p_a(i)=\sum _{k=0}^i{p}_f(k),i=1,2,\dots ,255$$
   其中，令$p_a(0)=0$。
4. 进行直方图均衡化计算，得到处理后图像的像素值$g(i,j)$为：$$g(i,j)=255\cdot p_a(k)$$

C++代码如下所示：

    cv::Mat image = cv::imread("Lena.bmp");
    cv::Mat src(image.size(), CV_8UC1);
    //转为灰度图像
    cv::cvtColor(image, src, CV_BGR2GRAY);

    cv::Mat dst(image.size(), CV_8UC1);
    float hf[256] = { 0 };
    for (int row = 0; row < src.rows; row++)
    {
        uchar *currentData = src.ptr<uchar>(row);
        for (int col = 0; col < src.cols; col++)
        {
            hf[*(currentData + col)] += 1;
        }
    }
    float pf[256] = { 0 };
    for (int i = 0; i < 256; i++)
    {
        pf[i] = hf[i] / (src.rows*src.cols);
    }
    float pa[256] = { 0 };
    for (int i = 1; i < 256; i++)
    {
        float sumNumber = 0;
        for (int j = 0; j < i+1; j++)
        {
            sumNumber += pf[j];
        }
        pa[i] = sumNumber;
    }
    for (int row = 0; row < dst.rows; row++)
    {
        uchar * currentData = dst.ptr<uchar>(row);
        for (int col = 0; col < dst.cols; col++)
        {
            *(currentData + col) = uchar(255 * pa[src.at<uchar>(row, col)]);
        }
    }

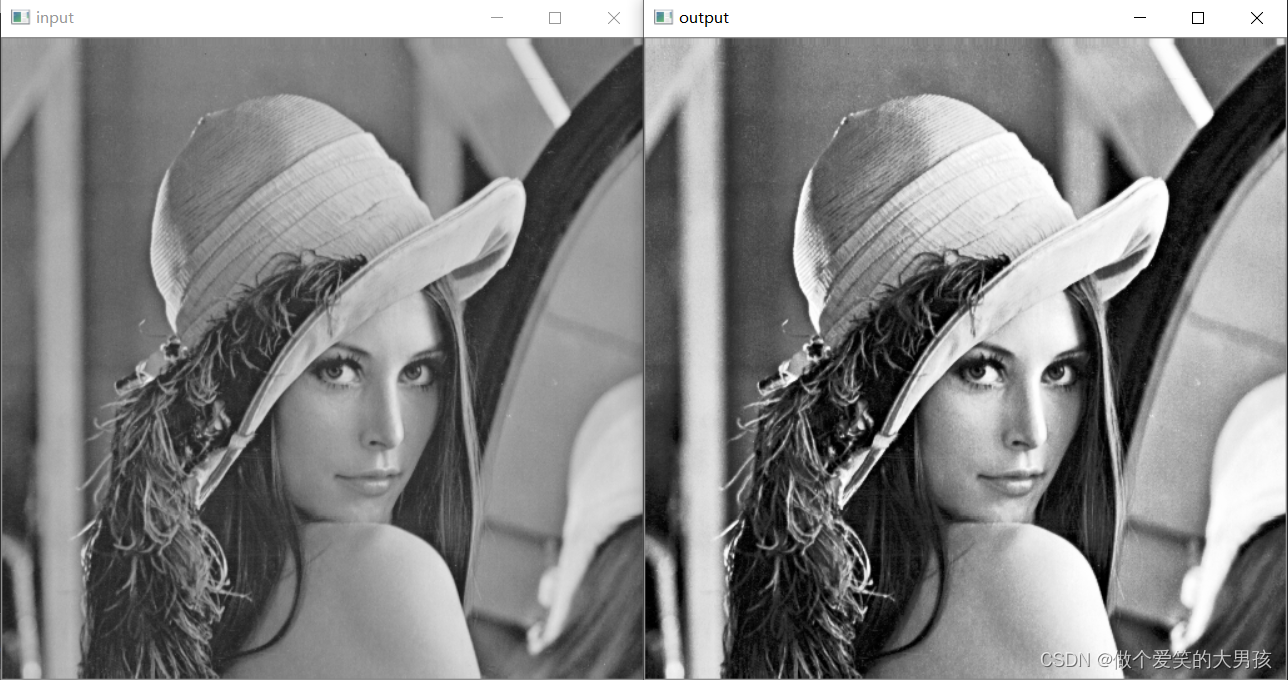
结果展示：