题目

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的大小，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1：

输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3 输出：4

解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ，因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意，因为它含 4
个 1 ，大于 n 的值 3 。

示例 2： 输入：strs = [“10”, “0”, “1”], m = 1, n = 1 输出：2 解释：最大的子集是 {“0”,
“1”} ，所以答案是 2 。

提示：

1 <= strs.length <= 600 1 <= strs[i].length <= 100 strs[i] 仅由 ‘0’ 和
‘1’ 组成 1 <= m, n <= 100

思路

本题仍然是01背包问题，因为strs数组里的元素，相当于就是物品，每个物品的个数都是一个，而m和n相当于是一个背包，两个维度的背包，不同的字符串长度就是不同大小的待装物品

典型的背包问题，只不过物品的重量有了两个维度

动规五部曲：

1. 确定dp数组和下标的含义
   dp[i][j]表示最多有 i 个0和 j 个 1 的 strs 的最大子集的大小为dp[i][j]
2. 确定递推公式
   dp[i][j] 可以从前一个strs里的字符串推导出来，strs里的字符串有zeros个0，有ones个1
   那么dp[i][j]就可以是dp[i - zeros][j - ones] + 1
   然后在遍历的时候，取dp[i][j]的最大值

dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1)

这里实际上是三维，还有一个维度是第几个字符串，dp[i-1][][]，dp[i][][]，但是可以用滚动数组的思想，去掉这一维，类似于01背包的一维公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

3. dp数组初始化
   01背包的dp数组初始化为 0 就可以，因为物品价值不会是负数，初始为0，可以保证递推的时候不会被dp[i][j]不会被初始值（0）覆盖，或者换个说法，保证一定会被背包价值覆盖
4. 确定遍历顺序
   01背包一维公式遍历顺序，外层遍历物品，内层倒序遍历背包大小
5. 举例推导dp数组
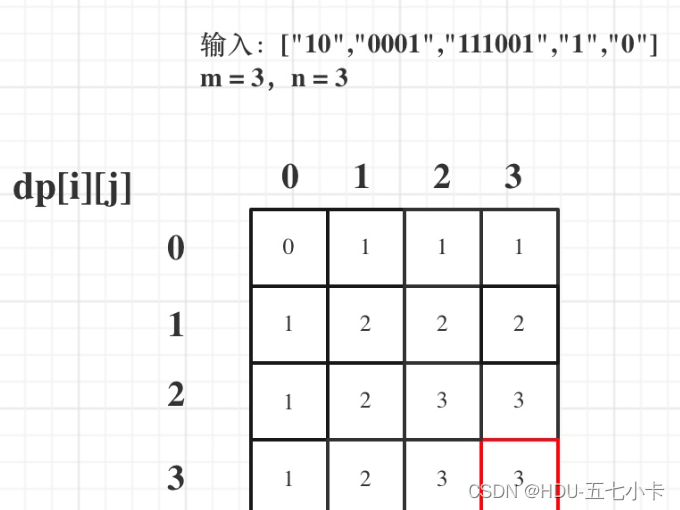
   以输入：[“10”,“0001”,“111001”,“1”,“0”]，m = 3，n = 3为例
   最后dp数组的状态如下所示：
   
   java代码如下：

class Solution{
	public int findMaxFornm(String[] s,int m, int n){
		//dp[i][j]表示i个0和j个1时的最大子集
		int[][] dp= new int[m+1][n+1];
		int ones,zeros;
		for(String str : strs){//遍历字符串数组中的每一个字符串，这里相当于遍历物品
			ones = 0;
			zeros = 0;
			for(char ch : str.toCharArray()){//将字符串str转化成字符数组，并用ch来遍历每一个字符
				if(ch == '0'){
					zeros++;
				} else {
					ones++;
				}
			}
			//倒序遍历背包容量，这里有两个维度表示容量
			for(int i = m; i >= zeros; i--){
				 for(int j = n; j >= ones; j--){
				 	dp[i][j] = Matn.max(dp[i][j], dp[i-zeros][j - ones] + 1);
				 }
			}
		}
		return dp[m][n];
	} 
}