PS：softmax回归损失函数梯度下降，求导部分没使用指示函数和向量，直接针对单变量进行推导。网上其他资料都比较抽象，找了很久没找到容易理解的，硬刚了几天终于整出来了。

一、前言

前面一篇文章《机器学习 逻辑回归(1)二分类》主要用于解决是与否的问题，有两种可能结果。

假设结果有多种可能，比如说，识别手写数字有0~9十种可能，怎么处理呢？

二分类与多分类的区别：

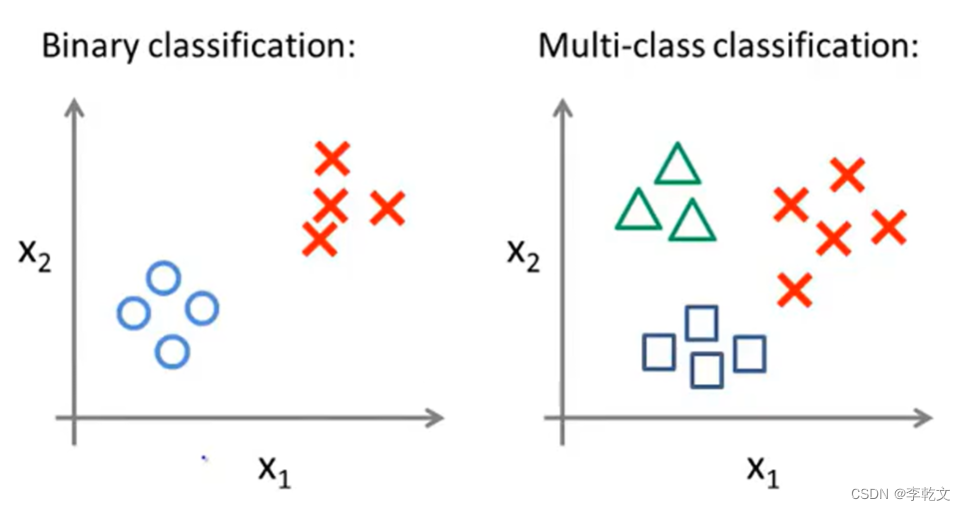
接下来让我们开始逻辑回归多类别分类的学习。

有一种方法，可以把N种类别取出一种，剩下的类别统一归为一类，当成二分类问题；然后换成另一类，剩下的归为一类，如此遍历，将多类别分类转成很多个二分类问题，这种方法叫一对余，在此只做简单介绍，我们不用这种方法。

我们使用softmax方法，也叫softmax回归。

二、假设函数

在二分类中，得到的是一个类似于概率的预测值。试想一下，如果得到的是每种类别的概率，那我们只需要取最大概率的类别就行了。

$x=\left[\begin{array}{cccc}{x}_0^{(1)}& x_0^{(2)}& ...& x_0^{(m)}\\ x_1^{(1)}& x_1^{(2)}& ...& x_1^{(m)}\\ x_2^{(1)}& x_2^{(2)}& ...& x_2^{(m)}\\ ⋮& ⋮& ...& ⋮\\ x_n^{(1)}& x_n^{(2)}& ...& x_n^{(m)}\end{array}\right]$

在此我们对$w$进行扩展，假设有k个类别，它也变成了一个k行n列的矩阵：
$w=\left[\begin{array}{ccccc}{w}_0^{(1)}& w_1^{(1)}& w_2^{(1)}& ...& w_n^{(1)}\\ w_0^{(2)}& w_1^{(2)}& w_2^{(2)}& ...& w_n^{(2)}\\ ...& ...& ...& ...& ...\\ w_0^{(k)}& w_1^{(k)}& w_2^{(k)}& ...& w_n^{(k)}\end{array}\right]$

第$i$个实例的预测结果为：

$h(x^{(i)})=w{x}^{(i)}=\left[\begin{array}{c}{w}^{(1)}{x}^{(i)}\\ w^{(2)}{x}^{(i)}\\ ⋮\\ w^{(k)}{x}^{(i)}\end{array}\right]$

这是个k行1列的矩阵，对应k个类别的预测值。

参考《softmax函数及其代码实现》，将k个预测值代入softmax函数，形成总和为1的概率分布。假设函数就成了
$$\begin{array}{r}h(x^{(i)})=softmax(w{x}^{(i)})\end{array}$$

def softmax(x):
    ex=np.exp(x)
    return ex/ex.sum()

先将矩阵里的每个值通过$f(x)=e^x$函数转化成非负数
$$\left[\begin{array}{c}{e}^{w^{(1)}{x}^{(i)}}\\ e^{w^{(2)}{x}^{(i)}}\\ ⋮\\ e^{w^{(k)}{x}^{(i)}}\end{array}\right]$$

再将其转成概率分布
$$\left[\begin{array}{c}\frac{e^{w^{(1)}{x}^{(i)}}}{{\sum }_{j=1}^k{e}^{w^{(j)}{x}^{(i)}}}\\ \frac{e^{w^{(2)}{x}^{(i)}}}{{\sum }_{j=1}^k{e}^{w^{(j)}{x}^{(i)}}}\\ ⋮\\ \frac{e^{w^{(k)}{x}^{(i)}}}{{\sum }_{j=1}^k{e}^{w^{(j)}{x}^{(i)}}}\end{array}\right]$$

这时候比较每个值，取最大值的下标则作为预测类别。

$h(x^{(i)}{)}_j$指的是第$j$个值，如$$h(x^{(i)}{)}_2=\frac{e^{w^{(2)}{x}^{(i)}}}{{\sum }_{j=1}^k{e}^{w^{(j)}{x}^{(i)}}}$$

三、One-Hot 独热编码

上面是One-Hot独热编码呢？举个栗子就一目了然。
假设类别有[鸡，鸭，狗] 3种动物：

值	编码
鸡	100
鸭	010
狗	001

实例$y=[3,1,2,3,\dots ]$，即 [ 狗，鸡，鸭，狗，… ]，用独热编码矩阵表示为：
$Y=\left[\begin{array}{ccc}0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ ⋮& ⋮& ⋮\end{array}\right]$

$Y_{y^{(i)}}^{(i)}=1$

如当$i=3$ 时，$Y_2^{(3)}=1$。

这样用假设函数求出各种类别的概率后，就能结合独热编码矩阵，计算出误差代价。

四、代价函数

在这里引入了交叉熵公式，softmax回归的代价函数是

$L=-{\sum }_{j=1}^k{Y}_j^{(i)}\ln (h(x^{(i)}{)}_j)$（一个实例样本）

由于经过softmax计算，$h(x^{(i)}{)}_j$的取值范围为$(0,1)$，L的函数图像为：

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0.0001, 1, 0.0001) #起点，终点，间距
y = -np.log(x)
plt.plot(x, y)
plt.show()

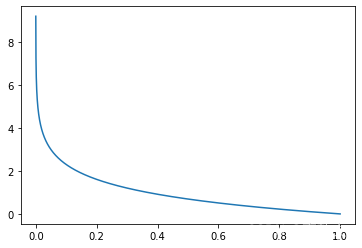
由此可见，当$Y_j^{(i)}=1$时，预测值$h(x^{(i)}{)}_j$越接近1，误差损失就越小。

那么总的代价函数则为
$$J=\frac{1}{m}\sum _{i=1}^{m}L=-\frac{1}{m}\sum _{i=1}^m\sum _{j=1}^k{Y}_j^{(i)}\ln (h(x^{(i)}{)}_j)$$

五、梯度下降

前面文章《逻辑回归(1)二分类》中已经说明：

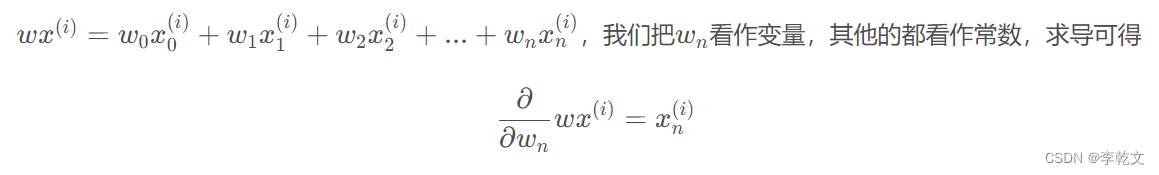
在此处，由于$w$是一个k行n列的矩阵，$w^{(c)}$对应对的就是上面的$w$，那么就有：

$$\frac{\partial }{\partial w_n^{(c)}}{w}^{(c)}{x}^{(i)}=x_n^{(i)}$$

下面用到的公式有：
$\ln \frac{M}{N}=\ln M-\ln N$
$\ln e^x=x$
$(\ln x{)}^{\prime }=\frac{1}{x}$
$(e^x{)}^{\prime }=e^x$

$$\begin{array}{rl}\frac{\partial J}{\partial w_n^{(c)}}& =-\frac{1}{m}\frac{\partial J}{\partial w_n^{(c)}}\sum _{i=1}^m\sum _{j=1}^k{Y}_j^{(i)}\ln (h(x^{(i)}{)}_j)\\ & =-\frac{1}{m}\frac{\partial J}{\partial w_n^{(c)}}\sum _{i=1}^m\sum _{j=1}^k{Y}_j^{(i)}\ln (\frac{e^{w^{(j)}{x}^{(i)}}}{{\sum }_{j=1}^k{e}^{w^{(j)}{x}^{(i)}}})\\ & =-\frac{1}{m}\frac{\partial J}{\partial w_n^{(c)}}\sum _{i=1}^m\sum _{j=1}^k{Y}_j^{(i)}(w^{(j)}{x}^{(i)}-\ln \sum _{j=1}^k{e}^{w^{(j)}{x}^{(i)}})\\ & =-\frac{1}{m}\frac{\partial J}{\partial w_n^{(c)}}\sum _{i=1}^m(\sum _{j=1}^k{Y}_j^{(i)}{w}^{(j)}{x}^{(i)}-\sum _{j=1}^k{Y}_j^{(i)}\ln \sum _{j=1}^k{e}^{w^{(j)}{x}^{(i)}})\\ & =-\frac{1}{m}\frac{\partial J}{\partial w_n^{(c)}}\sum _{i=1}^m(Y_1^{(i)}{w}^{(1)}{x}^{(i)}+Y_2^{(i)}{w}^{(2)}{x}^{(i)}+\cdots +Y_c^{(i)}{w}^{(c)}{x}^{(i)}+\cdots +Y_k^{(i)}{w}^{(k)}{x}^{(i)}-Y_1^{(i)}\ln \sum _{j=1}^k{e}^{w^{(j)}{x}^{(i)}}+Y_2^{(i)}\ln \sum _{j=1}^k{e}^{w^{(j)}{x}^{(i)}}+\cdots +Y_k^{(i)}\ln \sum _{j=1}^k{e}^{w^{(j)}{x}^{(i)}})\\ & =-\frac{1}{m}\sum _{i=1}^m(Y_c^{(i)}{x}_n^{(i)}-Y_1^{(i)}\frac{1}{{\sum }_{j=1}^k{e}^{w^{(j)}{x}^{(i)}}}{e}^{w^{(c)}{x}^{(i)}}{x}_n^{(i)}-Y_2^{(i)}\frac{1}{{\sum }_{j=1}^k{e}^{w^{(j)}{x}^{(i)}}}{e}^{w^{(c)}{x}^{(i)}}{x}_n^{(i)}-\cdots -Y_k^{(i)}\frac{1}{{\sum }_{j=1}^k{e}^{w^{(j)}{x}^{(i)}}}{e}^{w^{(c)}{x}^{(i)}}{x}_n^{(i)})\\ & =-\frac{1}{m}\sum _{i=1}^m(Y_c^{(i)}{x}_n^{(i)}-\frac{e^{w^{(c)}{x}^{(i)}}}{{\sum }_{j=1}^k{e}^{w^{(j)}{x}^{(i)}}}{x}_n^{(i)}(Y_1^{(i)}+Y_2^{(i)}+\cdots +Y_k^{(i)}))\\ & =-\frac{1}{m}\sum _{i=1}^m(Y_c^{(i)}{x}_n^{(i)}-\frac{e^{w^{(c)}{x}^{(i)}}}{{\sum }_{j=1}^k{e}^{w^{(j)}{x}^{(i)}}}{x}_n^{(i)})\\ & =-\frac{1}{m}\sum _{i=1}^m{x}_n^{(i)}(Y_c^{(i)}-\frac{e^{w^{(c)}{x}^{(i)}}}{{\sum }_{j=1}^k{e}^{w^{(j)}{x}^{(i)}}})\end{array}$$

六、原生代码实现

这次我们使用鸢尾花数据集

6.1 加载并查看数据

from sklearn import datasets  # 导入库
dataset = datasets.load_iris()  # 导入鸢尾花数据
print(dataset.data.shape,dataset.target.shape)  # (150, 4) (150,)
print(dataset.feature_names)  # [花萼长，花萼宽，花瓣长，花瓣宽]
print(dataset.target_names)
# print(iris.DESCR) #查看数据集描述

运行结果：
可以看到有[花萼长，花萼宽，花瓣长，花瓣宽]4个特征，以及['setosa' 'versicolor' 'virginica']三个类别。

(150, 4) (150,)
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
['setosa' 'versicolor' 'virginica']

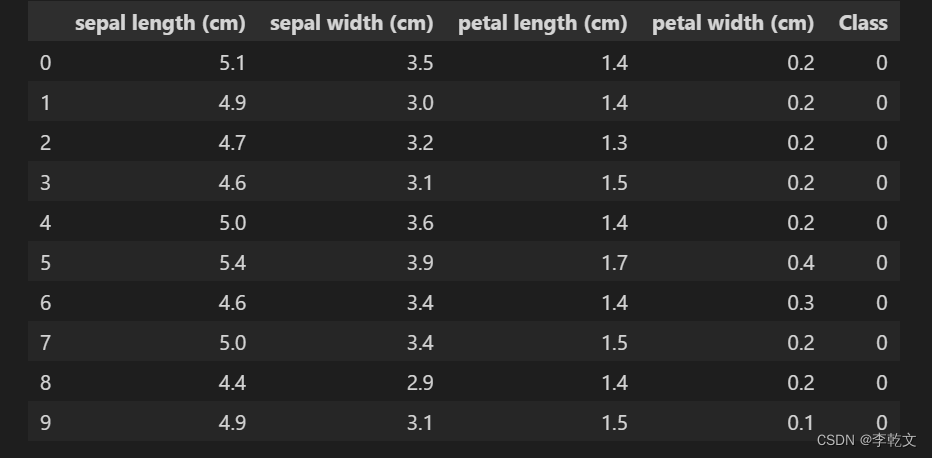
查看前10条数据

import pandas as pd
data_df = pd.DataFrame(dataset.data, columns=dataset.feature_names)
data_df['Class'] = dataset.target
data_df.head(10) #查看前10条数据

运行结果：

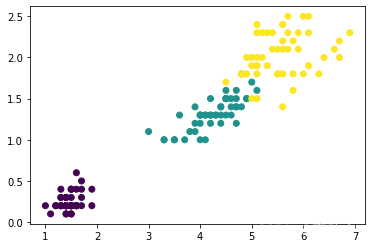
我们以花瓣长度和宽度作为x和y变量，大致查看一下分布：

import matplotlib.pyplot as plt
plt.scatter(
    data_df['petal length (cm)'], #x坐标
    data_df['petal width (cm)'], #y坐标
    c=data_df['Class'],#颜色
)
plt.show()

运行结果：

6.2 添加前置与数据分割

添加x0=1的前置，然后将数据分割成训练数据与验证数据。

import numpy as np
np.set_printoptions(suppress=True) #numpy不使用科学计数法
from sklearn.model_selection import train_test_split

X, Y = datasets.load_iris(return_X_y=True)

#添加前置 x0=1
temp = np.ones([X.shape[0],X.shape[1]+1])
temp[:,1:] = X #第[0]行到最后一行的(第[1]列到最后一列)赋值为X
X = temp

# 将数据分割为训练和验证数据，都有特征和预测目标值
# 分割基于随机数生成器。为random_state参数提供一个数值可以保证每次得到相同的分割
X_train, X_test, y_train, y_test = train_test_split(X, Y, random_state = 0)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

运行结果：

(112, 5) (38, 5) (112,) (38,)

6.3 迭代训练

#独热编码函数
def one_hot(y): 
    one_hot = np.zeros((m, k))
    one_hot[np.arange(m), y.T] = 1
    return one_hot

#softmax函数
def softmax(scores):
    sum_exp = np.sum(np.exp(scores), axis=0)
    softmax = np.exp(scores) / sum_exp
    return softmax

#损失函数
def loss(y_one_hot,probs):
    return (-1/m)*np.sum(y_one_hot*np.log(probs))


learn_rate=0.1 #学习率
m=X_train.shape[0]
n=X_train.shape[1] #由于添加了前置，这里的n等于文章中的n+1
k=data_df['Class'].unique().shape[0] #种类数量

np.random.seed(1)
w=(np.random.random([k,n])-0.5)*2 #初始化参数w，k行n列，取值范围[-1,1)
# y_train=y_train.reshape([1,m])

count=0 #迭代次数
plt_epoch=[]
plt_loss=[]

# 计算 one-hot 矩阵
y_one_hot = one_hot(y_train)
y_one_hot=y_one_hot.T # k行m列

#迭代
for i in range(10000):

    scores=w.dot(X_train.T) # 分数矩阵，k行m列，由于数据集是m行n列，这里的X_train.T就是文章中的x
    probs=softmax(scores) #进行softmax计算,k行m列

    w_C=(-learn_rate/m)*(y_one_hot-probs).dot(X_train) #k行n列
    
    
    if count%100==0:
        # 每迭代100次则输出误差值
        ls=loss(y_one_hot,probs)
        print('epoch:',count,'loss:',ls)
        plt_epoch.append(count)
        plt_loss.append(ls)

    #若w变化不大，则暂停迭代，模型训练完成
    if (np.abs(w_C)<0.001).all():
        print('最终w变化量：',w_C)
        break
    count+=1
    w-=w_C

print('迭代次数：',count)
print('w权重：',w)

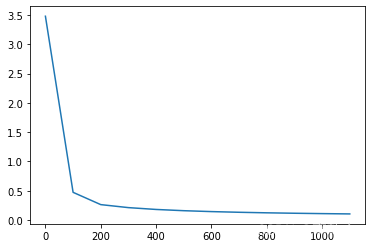
#绘制迭代次数与损失函数的关系
plt.plot(plt_epoch,plt_loss)

运行结果：

epoch: 0 loss: 3.4770110920562307
epoch: 100 loss: 0.47362291421521374
epoch: 200 loss: 0.2642328678118655
epoch: 300 loss: 0.21304305853900296
epoch: 400 loss: 0.18173915290674772
epoch: 500 loss: 0.1605547956098286
epoch: 600 loss: 0.14522407403143245
epoch: 700 loss: 0.13357920108443666
epoch: 800 loss: 0.1244066715794026
epoch: 900 loss: 0.11697518958289194
epoch: 1000 loss: 0.11081781173685108
epoch: 1100 loss: 0.1056222274323396
最终w变化量： [[-0.00012538 -0.00029019 -0.00061384  0.00080699  0.00038747]
 [-0.00039937 -0.00030874  0.00001068  0.00019287  0.00054193]
 [ 0.00052475  0.00059893  0.00060315 -0.00099986 -0.0009294 ]]
迭代次数： 1109
w权重： [[ 0.23633112  1.30617392  1.0862866  -3.09701251 -1.94803157]
 [ 0.01764411  0.83869538 -0.68038914 -0.27560502 -1.39762578]
 [-1.396865   -1.96126088 -2.30564276  3.52705249  1.77157779]]

6.4 验证数据

y_predict = np.argmax(softmax(w.dot(X_test.T)), axis=0)

print('预测：',y_predict)
print('实际：',y_test)
print('误差：',y_predict-y_test)

运行结果：

预测： [2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 2 0 2 2 1 0 2]
实际： [2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0 1]
误差： [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1]

七、sklearn代码实现

from sklearn.linear_model import LogisticRegression
import joblib

#初始化模型
lr_model = LogisticRegression()
#训练
lr_model.fit(X_train, y_train)

#保持模型
joblib.dump(lr_model, './LogisticRegression.model')

#加载模型，在实际应用中直接加载已训练好的模型
lr_model = joblib.load('./LogisticRegression.model')
 
#预测
y_pred = lr_model.predict(X_test)

print("Prediction on test set:", y_pred)
print("Score on test set:", lr_model.score(X_test, y_test))

运行结果：

Prediction on test set: [2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0 2]
Score on test set: 0.9736842105263158

八、参考资料

《softmax回归推导及python实例分析》
《Softmax 回归原理与实现》