文章目录
- 二叉搜索树
- 1. 概念
- 2. 模拟实现二叉搜索树
- 2.1 准备工作 创建类
- 2.2 查找方法
- 2.3 插入方法
- 2.4 删除方法
- 3. 性能分析
二叉搜索树
前言 :
1. 概念
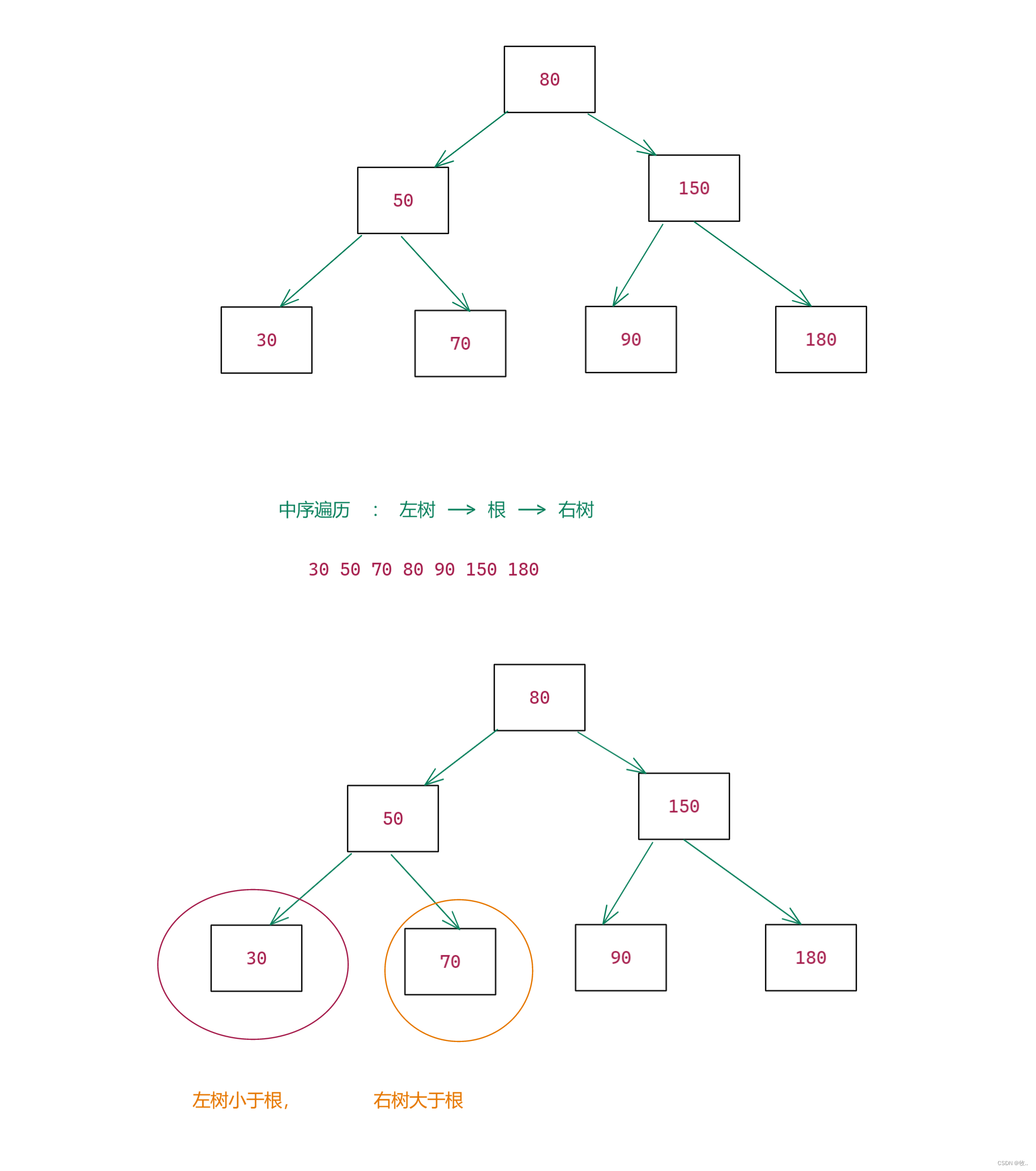
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
概念啥的看看就行了,之前二叉树的时候可能就已经见过了, 下面我们直接来实现我们自己的二叉搜索树
2. 模拟实现二叉搜索树
2.1 准备工作 创建类
这里我们创建一个 BinarySearchTree 和 内部类 TreeNode
2.2 查找方法
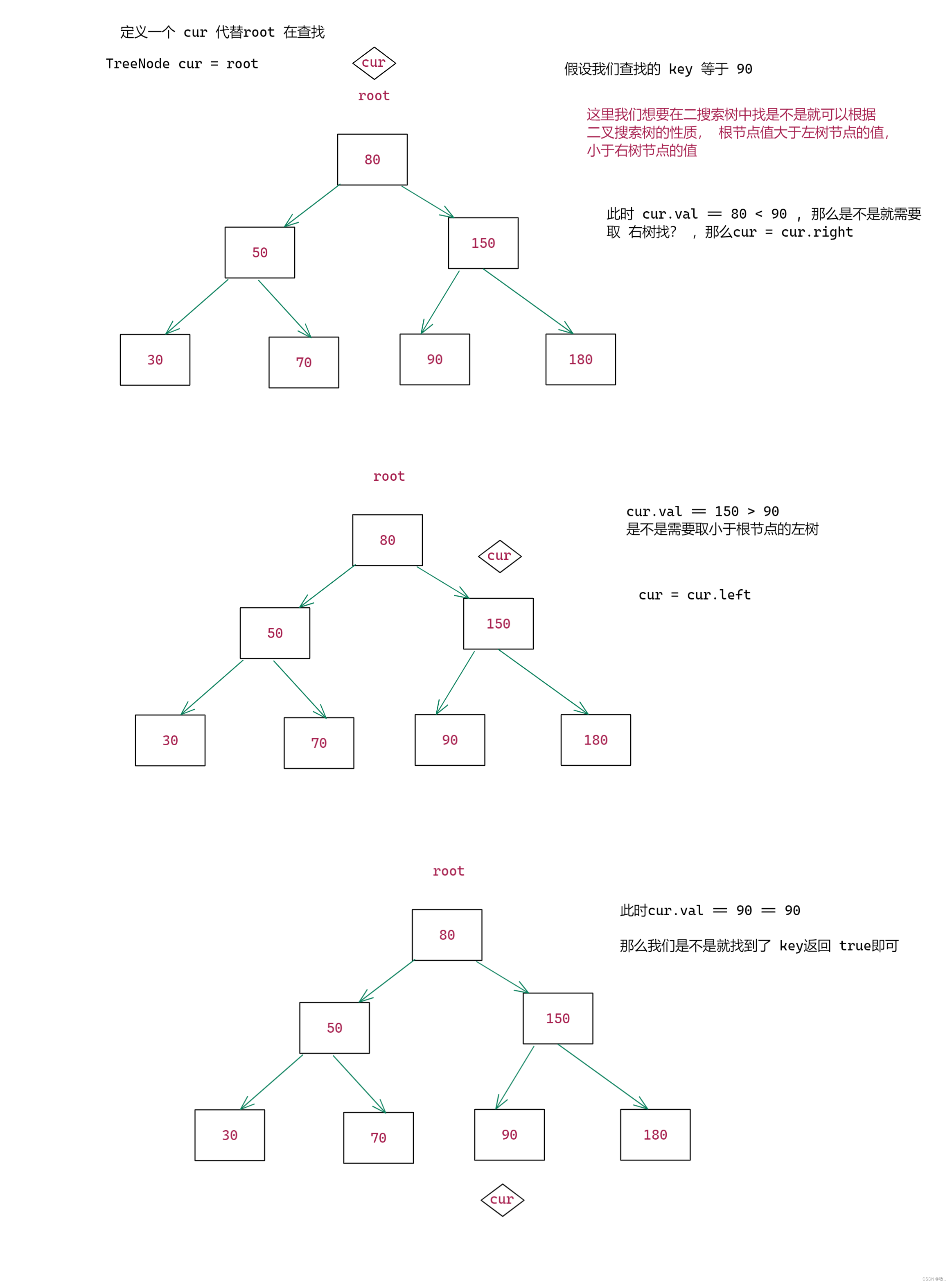
代码实现 :

查找功能就完成了,下面完成插入方法
2.3 插入方法
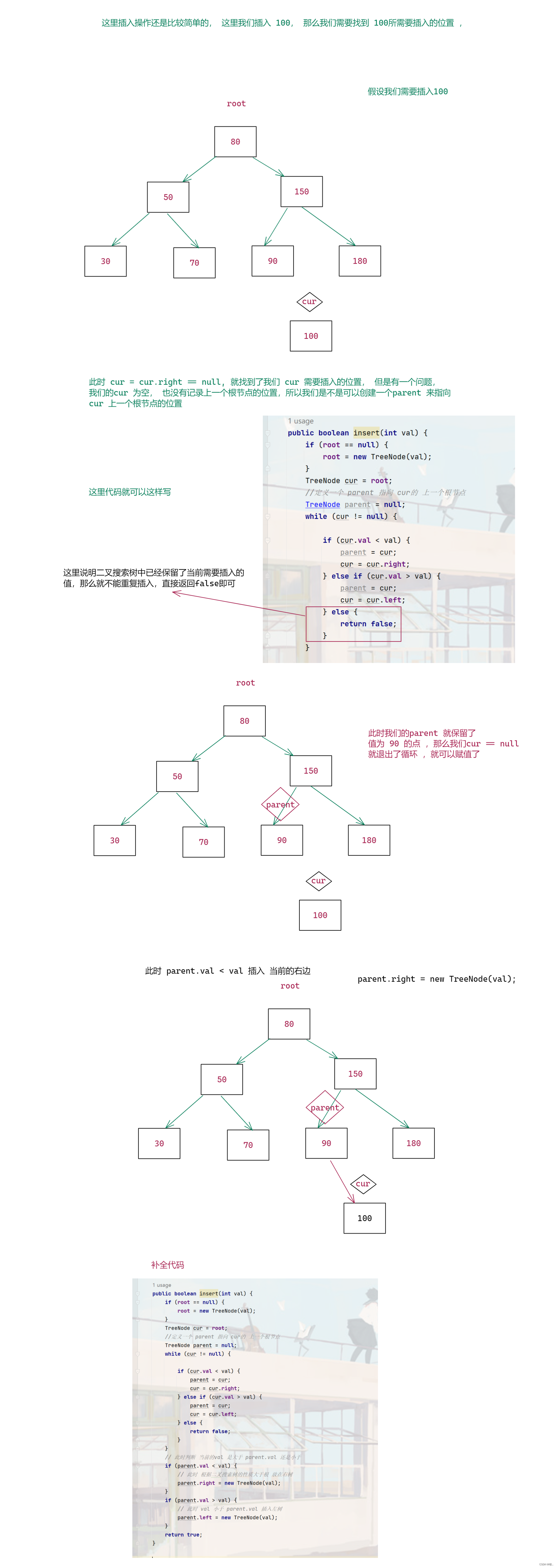
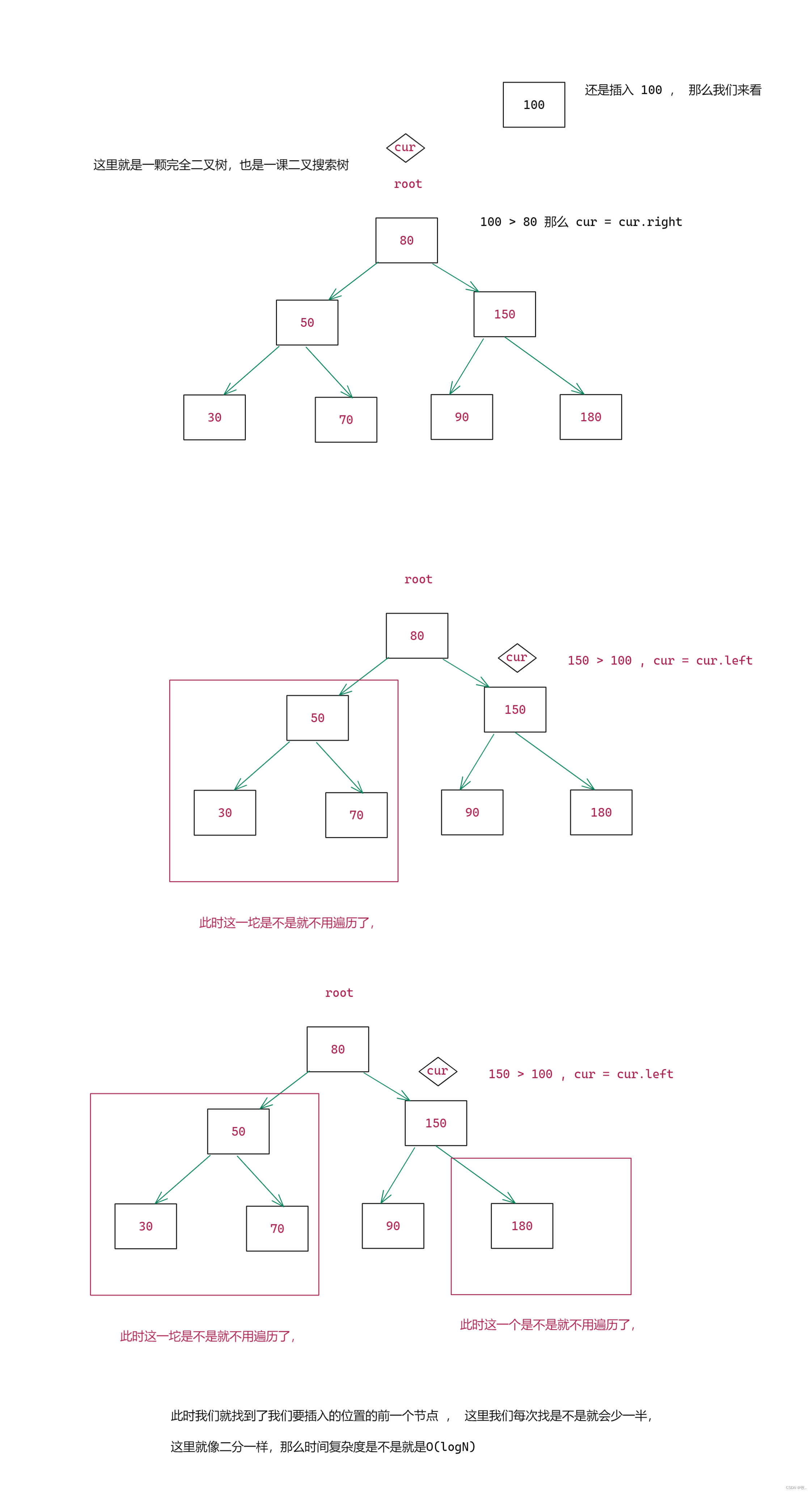
补充: 这里我们 假设我们的二叉搜索树是一颗完全二叉树,那么这里我们插入的时间复杂度是不是就是O(logN)
单分支的情况 加 了解 AVL 树
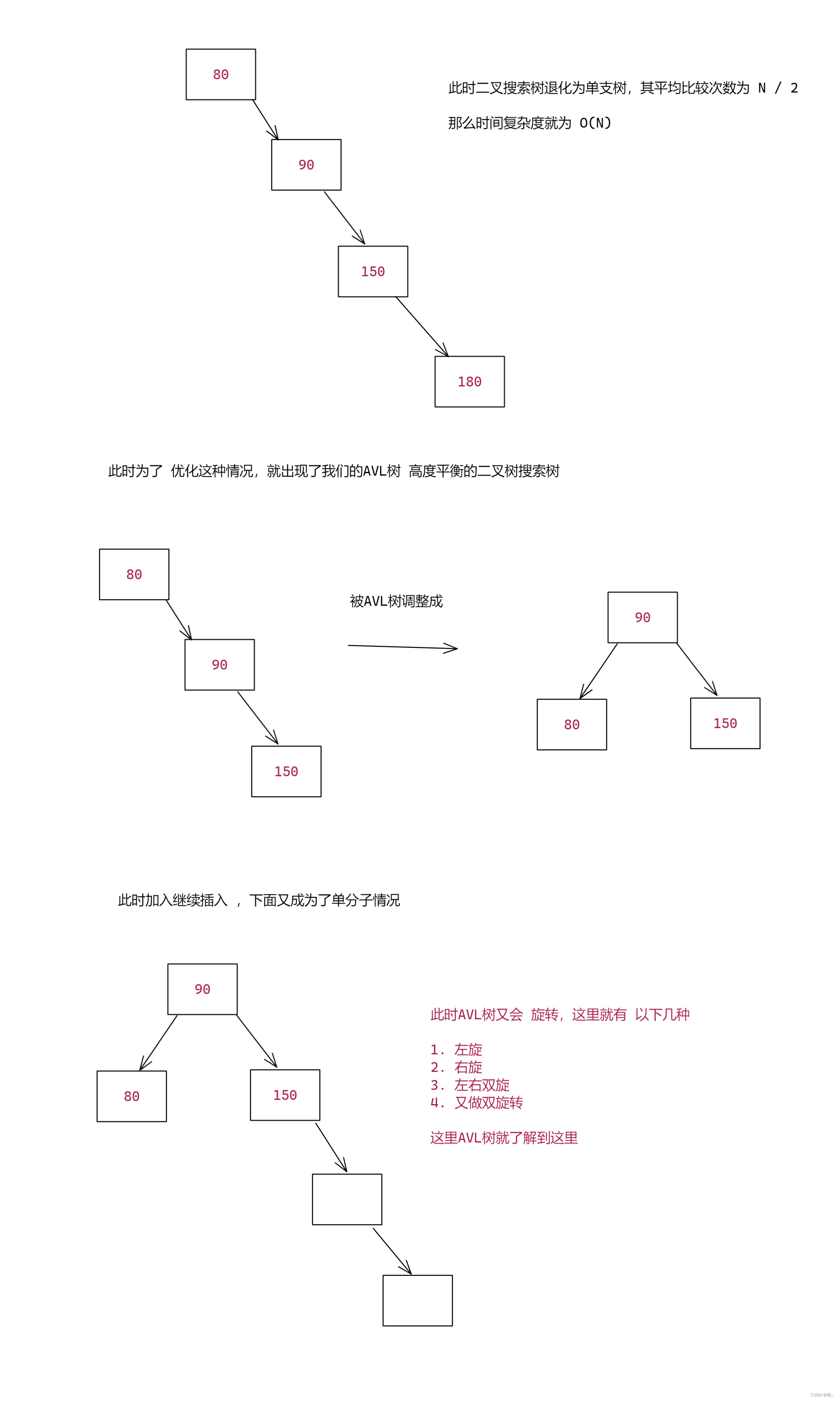
补充 : 这里忘记 讲 了 这里 二叉搜索树是空树的情况,那么我们直接让 root = new TreeNode(val) 即可,创建第一个节点
最终代码 :
public boolean insert(int val) {
if (root == null) {
root = new TreeNode(val);
}
TreeNode cur = root;
//定义一个 parent 指向 cur的 上一个根节点
TreeNode parent = null;
while (cur != null) {
if (cur.val < val) {
parent = cur;
cur = cur.right;
} else if (cur.val > val) {
parent = cur;
cur = cur.left;
} else {
return false;
}
}
// 此时判断 当前的val 是大于 parent.val 还是小于
if (parent.val < val) {
// 此时 根据二叉搜索树的性质大于根 放在右树
parent.right = new TreeNode(val);
}
if (parent.val > val) {
// 此时 val 小于 parent.val 插入左树
parent.left = new TreeNode(val);
}
return true;
}
下面就来学习一下,二叉搜索树中难一点的方法删除
2.4 删除方法
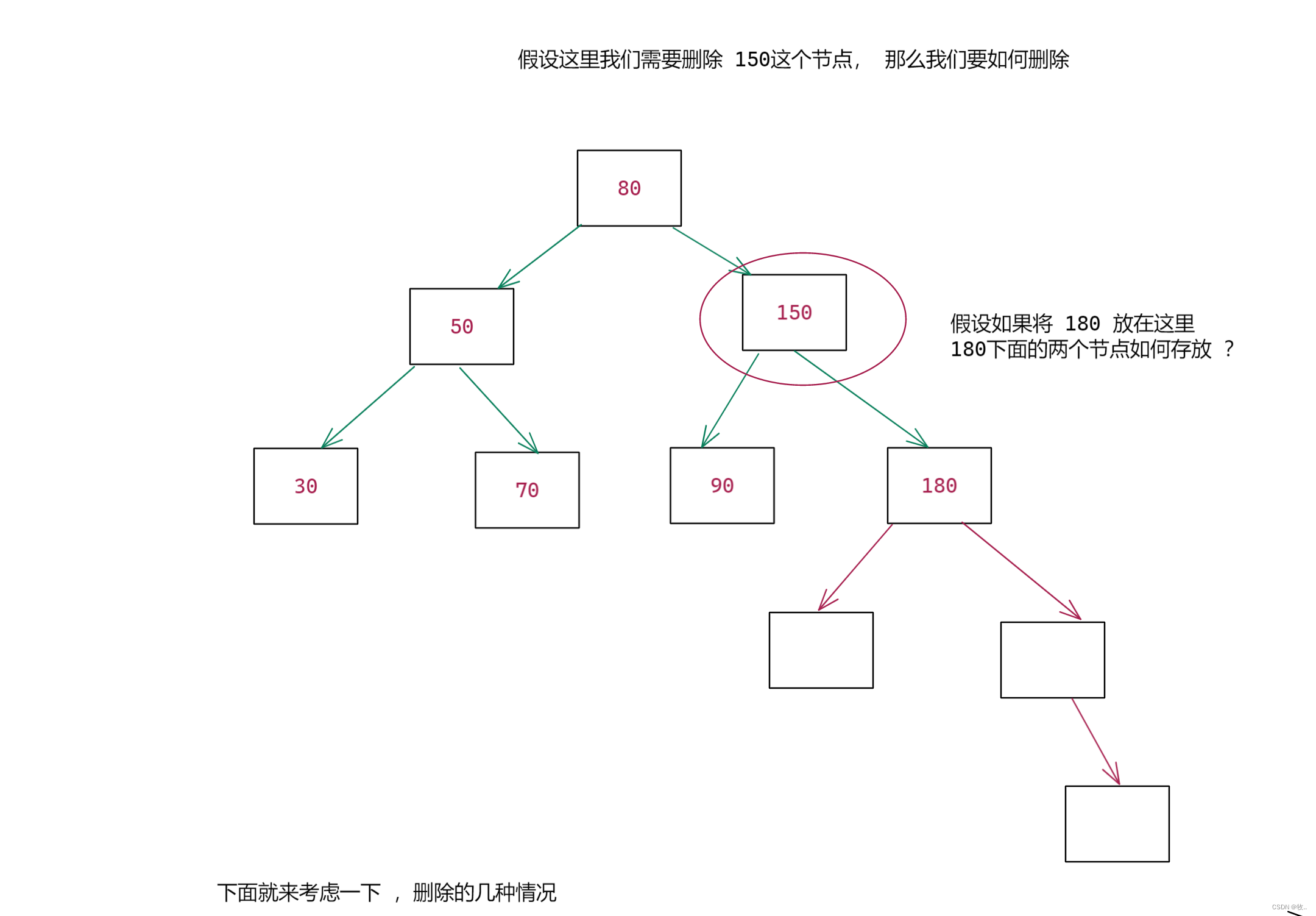
删除操作,算我们实现二叉搜索树中唯一难一点的操作这里需要分三种情况
图一:
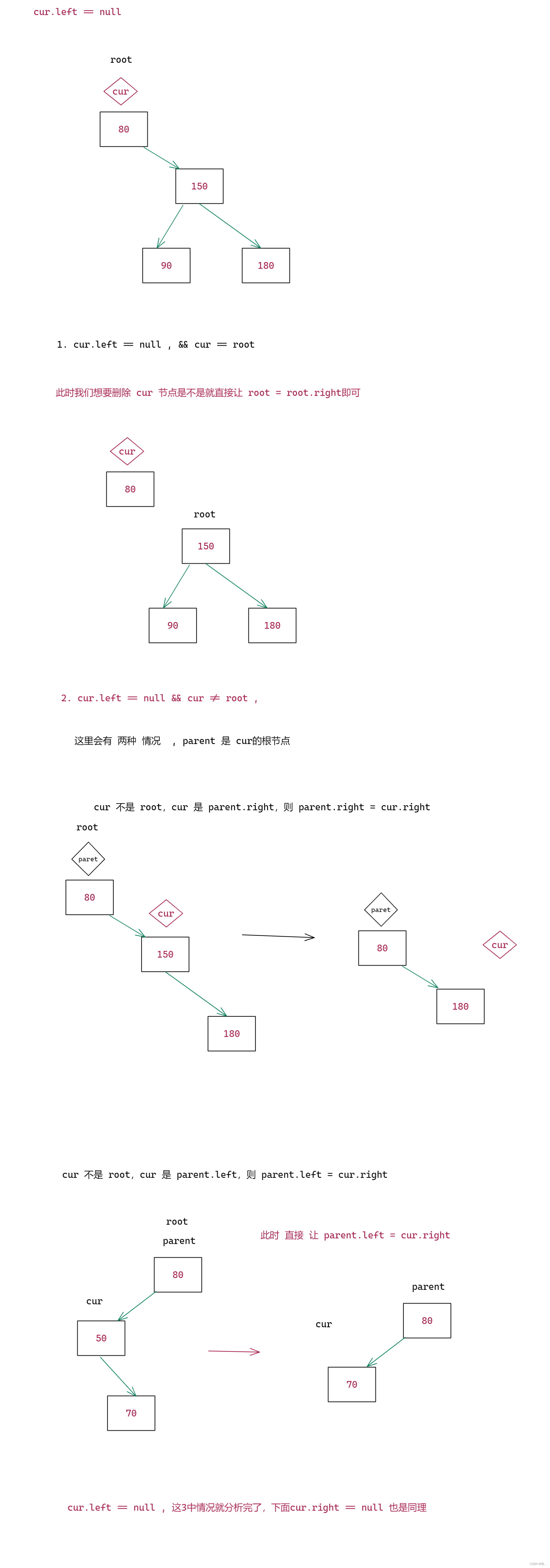
图二 : cur.left == null
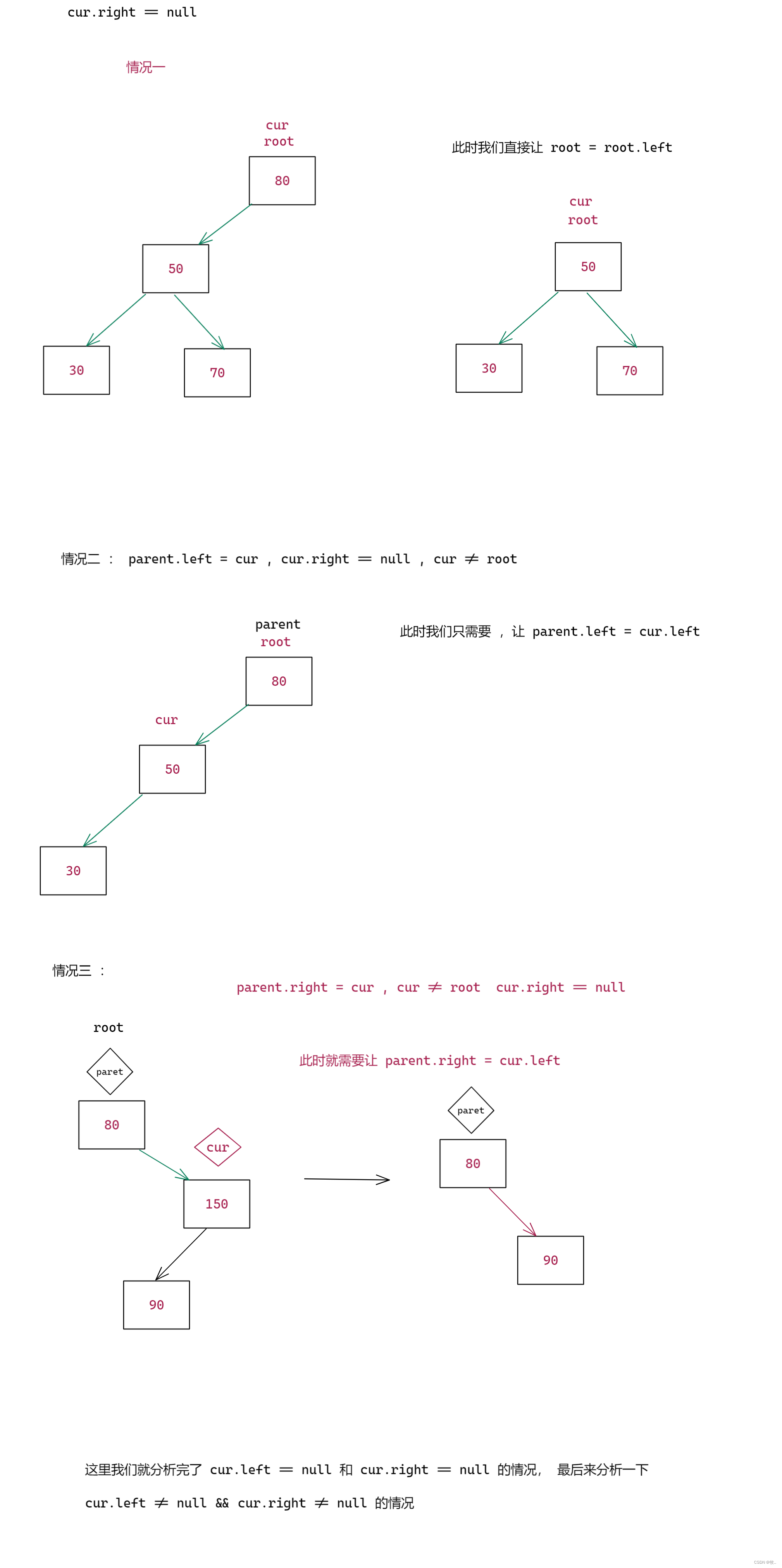
图三 : cur.right == null
图四 : cur.left != null && cur.right != null
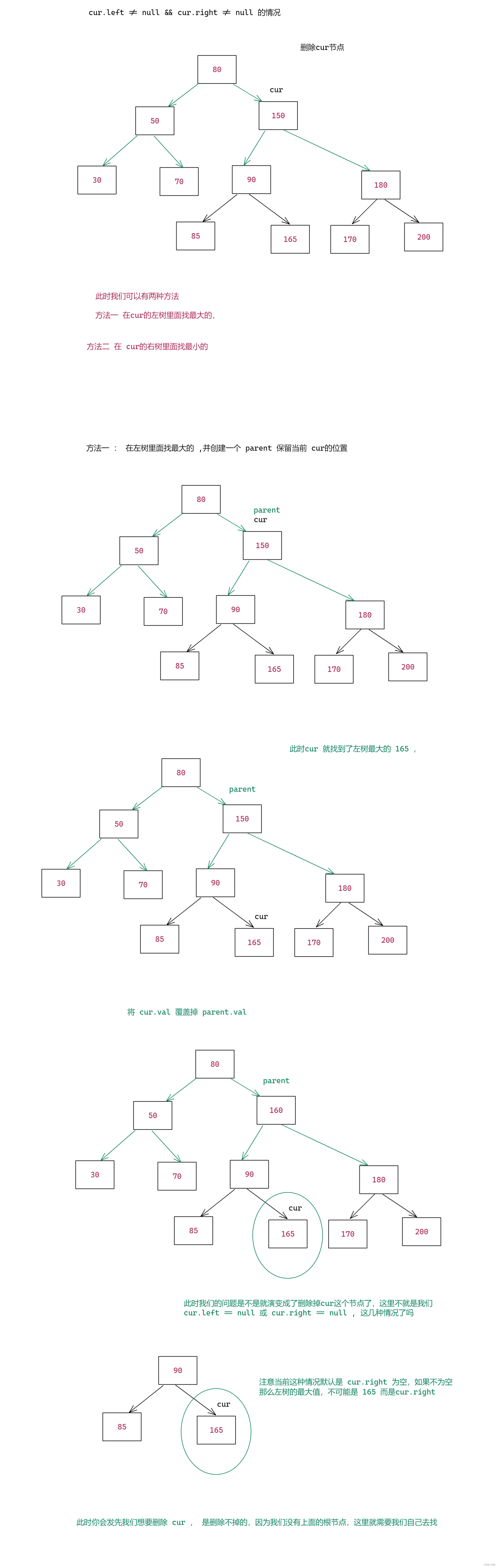
这里在右树中找最小的 可以自己画图分析 ,因为是一样的, 这里就留一个作业, 或者看下面的代码实现, 我们图是以找左树最大的,代码以找右树最小的 。
图一 :
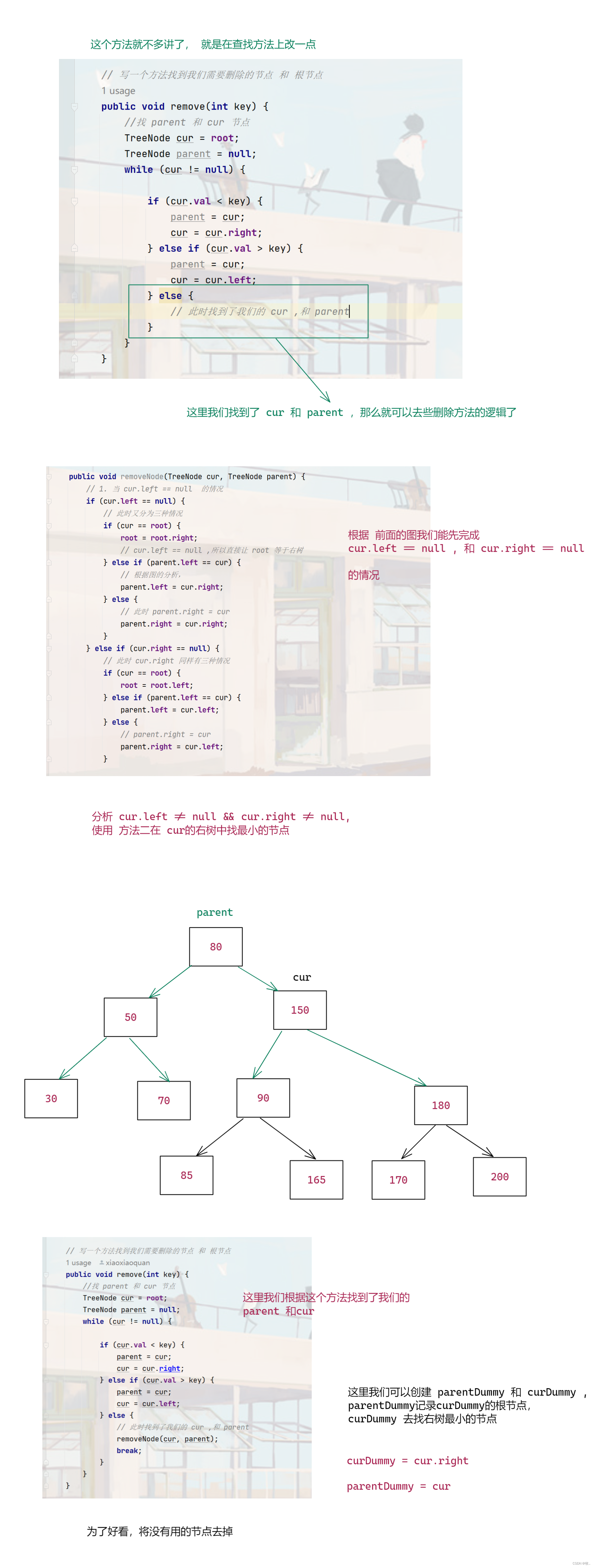
图二 :
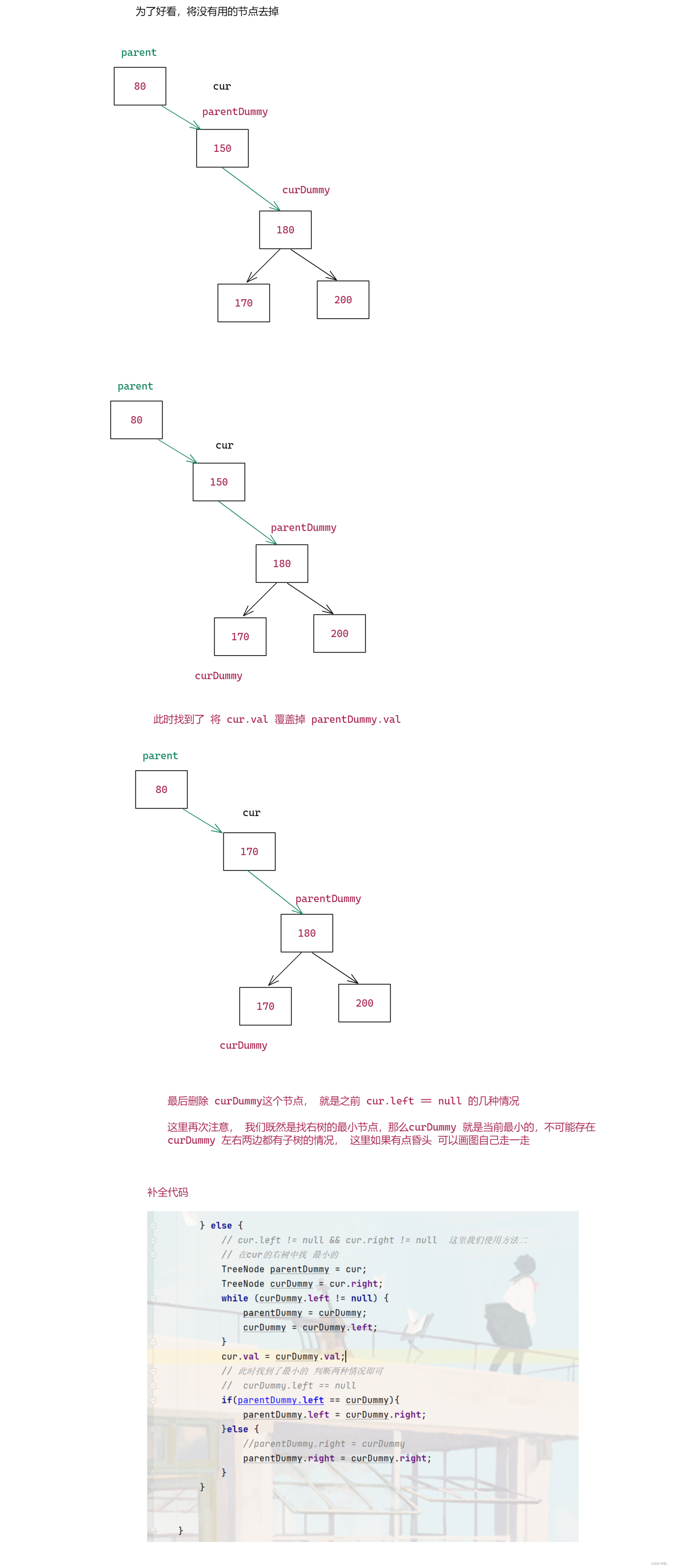
删除总代码:
// 写一个方法找到我们需要删除的节点 和 根节点
public void remove(int key) {
//找 parent 和 cur 节点
TreeNode cur = root;
TreeNode parent = null;
while (cur != null) {
if (cur.val < key) {
parent = cur;
cur = cur.right;
} else if (cur.val > key) {
parent = cur;
cur = cur.left;
} else {
// 此时找到了我们的 cur ,和 parent
removeNode(cur, parent);
break;
}
}
}
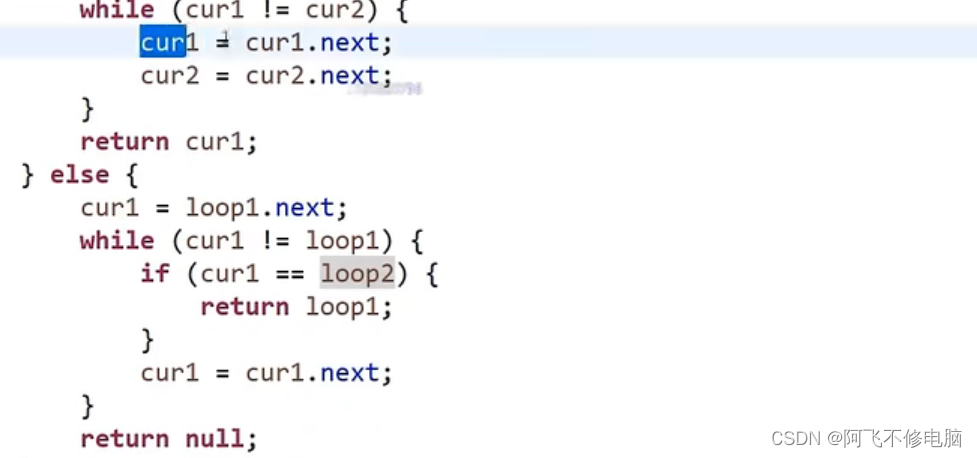
public void removeNode(TreeNode cur, TreeNode parent) {
// 1. 当 cur.left == null 的情况
if (cur.left == null) {
// 此时又分为三种情况
if (cur == root) {
root = root.right;
// cur.left == null ,所以直接让 root 等于右树
} else if (parent.left == cur) {
// 根据图的分析,
parent.left = cur.right;
} else {
// 此时 parent.right = cur
parent.right = cur.right;
}
} else if (cur.right == null) {
// 此时 cur.right 同样有三种情况
if (cur == root) {
root = root.left;
} else if (parent.left == cur) {
parent.left = cur.left;
} else {
// parent.right = cur
parent.right = cur.left;
}
} else {
// cur.left != null && cur.right != null 这里我们使用方法二
// 在cur的右树中找 最小的
TreeNode parentDummy = cur;
TreeNode curDummy = cur.right;
while (curDummy.left != null) {
parentDummy = curDummy;
curDummy = curDummy.left;
}
cur.val = curDummy.val;
// 此时找到了最小的 判断两种情况即可
// curDummy.left == null
if (parentDummy.left == curDummy) {
parentDummy.left = curDummy.right;
} else {
//parentDummy.right = curDummy
parentDummy.right = curDummy.right;
}
}
}
此时我们的二叉搜索的 查找新增删除方法就完成了.
附上代码:
public class BinarySearchTree {
static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public TreeNode root;
public TreeNode search(int key) {
TreeNode cur = root;
while (cur != null) {
if (cur.val < key) {
// 此时 key 大于 根进入 右树找
cur = cur.right;
} else if (cur.val > key) {
// 此时 ken 小于 根进入 左树找
cur = cur.left;
} else {
// 此时说明找到了 返回 当前节点地址;
return cur;
}
}
// 此时说明没有找到
return null;
}
public boolean insert(int val) {
if (root == null) {
root = new TreeNode(val);
}
TreeNode cur = root;
//定义一个 parent 指向 cur的 上一个根节点
TreeNode parent = null;
while (cur != null) {
if (cur.val < val) {
parent = cur;
cur = cur.right;
} else if (cur.val > val) {
parent = cur;
cur = cur.left;
} else {
return false;
}
}
// 此时判断 当前的val 是大于 parent.val 还是小于
if (parent.val < val) {
// 此时 根据二叉搜索树的性质大于根 放在右树
parent.right = new TreeNode(val);
}
if (parent.val > val) {
// 此时 val 小于 parent.val 插入左树
parent.left = new TreeNode(val);
}
return true;
}
// 写一个方法找到我们需要删除的节点 和 根节点
public void remove(int key) {
//找 parent 和 cur 节点
TreeNode cur = root;
TreeNode parent = null;
while (cur != null) {
if (cur.val < key) {
parent = cur;
cur = cur.right;
} else if (cur.val > key) {
parent = cur;
cur = cur.left;
} else {
// 此时找到了我们的 cur ,和 parent
removeNode(cur, parent);
break;
}
}
}
public void removeNode(TreeNode cur, TreeNode parent) {
// 1. 当 cur.left == null 的情况
if (cur.left == null) {
// 此时又分为三种情况
if (cur == root) {
root = root.right;
// cur.left == null ,所以直接让 root 等于右树
} else if (parent.left == cur) {
// 根据图的分析,
parent.left = cur.right;
} else {
// 此时 parent.right = cur
parent.right = cur.right;
}
} else if (cur.right == null) {
// 此时 cur.right 同样有三种情况
if (cur == root) {
root = root.left;
} else if (parent.left == cur) {
parent.left = cur.left;
} else {
// parent.right = cur
parent.right = cur.left;
}
} else {
// cur.left != null && cur.right != null 这里我们使用方法二
// 在cur的右树中找 最小的
TreeNode parentDummy = cur;
TreeNode curDummy = cur.right;
while (curDummy.left != null) {
parentDummy = curDummy;
curDummy = curDummy.left;
}
cur.val = curDummy.val;
// 此时找到了最小的 判断两种情况即可
// curDummy.left == null
if (parentDummy.left == curDummy) {
parentDummy.left = curDummy.right;
} else {
//parentDummy.right = curDummy
parentDummy.right = curDummy.right;
}
}
}
public void inorder(TreeNode root) {
if (root == null) {
return;
}
// 中序遍历 左 -> 根 -> 右
inorder(root.left);
System.out.print(root.val + " ");
inorder(root.right);
}
}
下面我们测试一下
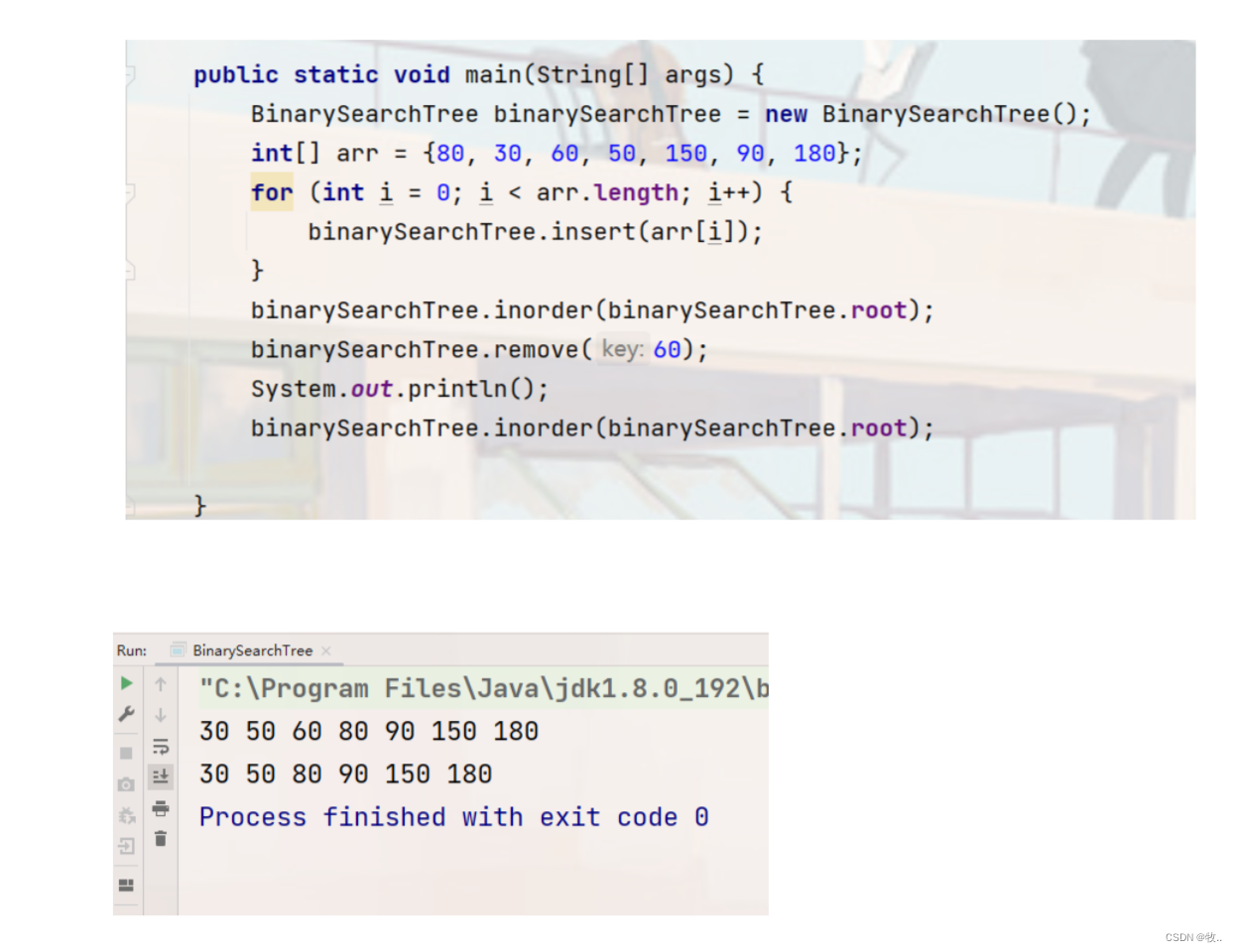
完美
3. 性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树
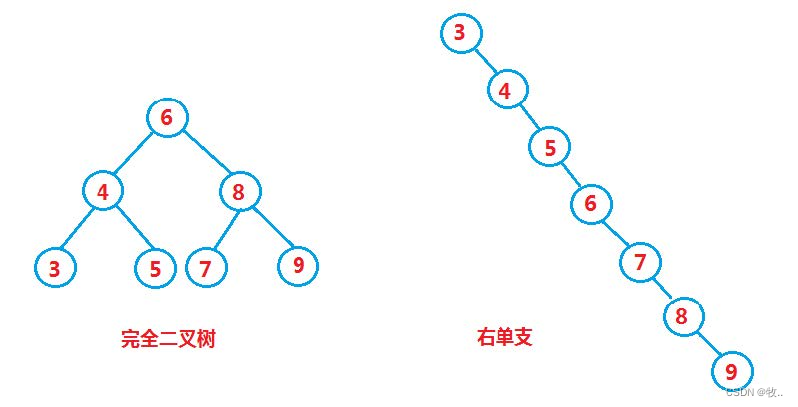
最优情况下,二叉搜索树为完全二叉树,其平均比较次数为:
最差情况下,二叉搜索树退化为单支树,其平均比较次数为:
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,都可以
是二叉搜索树的性能最佳?
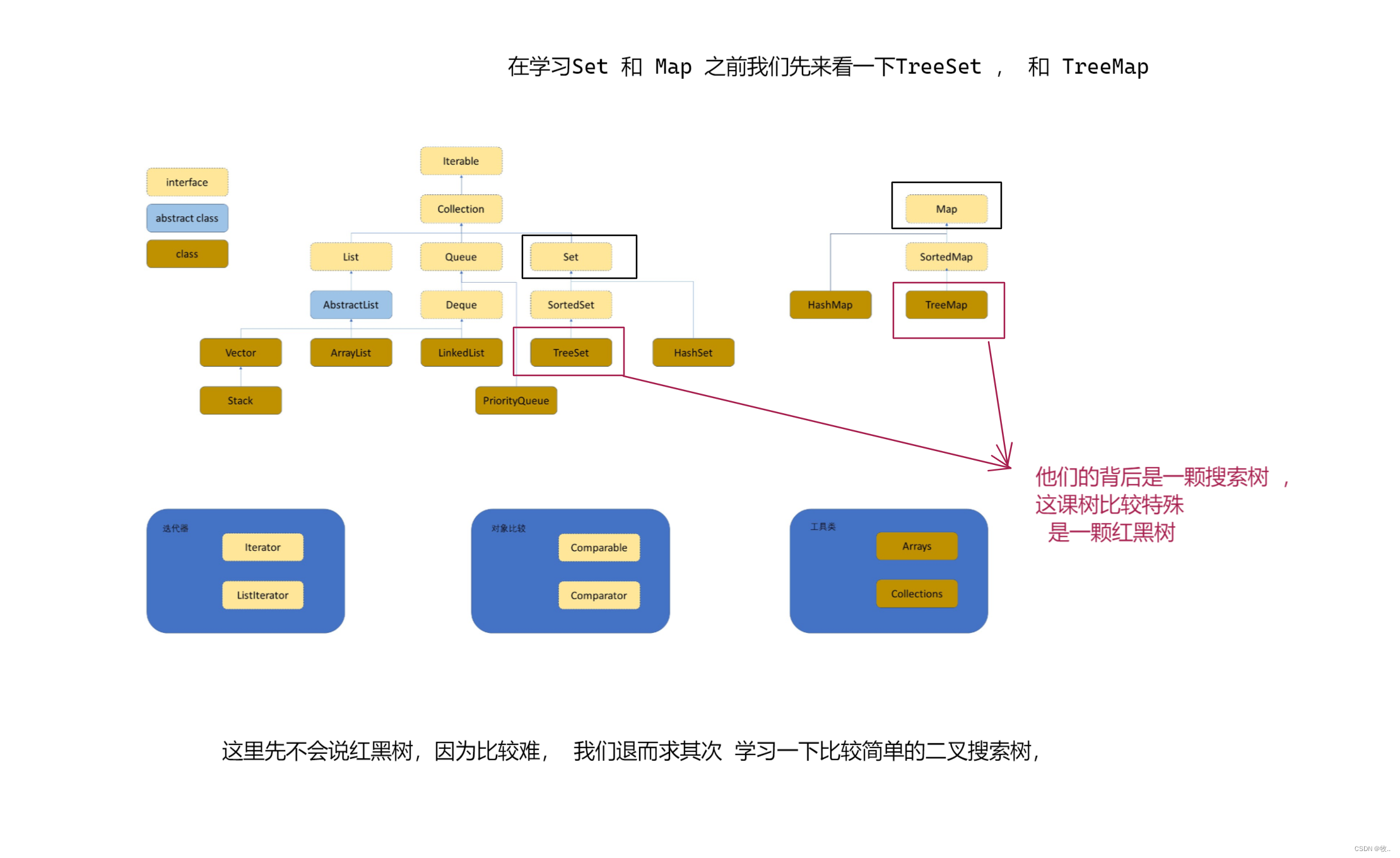
这里学习二叉搜索树 ,主要是为下文的 Set 和 Map 做准备
TreeMap 和 TreeSet 即 java 中利用搜索树实现的 Map 和 Set;实际上用的是红黑树,而红黑树是一棵近似平衡的
二叉搜索树,即在二叉搜索树的基础之上 + 颜色以及红黑树性质验证,这里红黑树比较难,需要我们知识的沉淀 ,那么再后续再来说我们的AVL树和红黑树…
下文 : Map 和 Set