目录

介绍：

实现原理：

简答来说：

例子

模板（C++）

---

介绍：

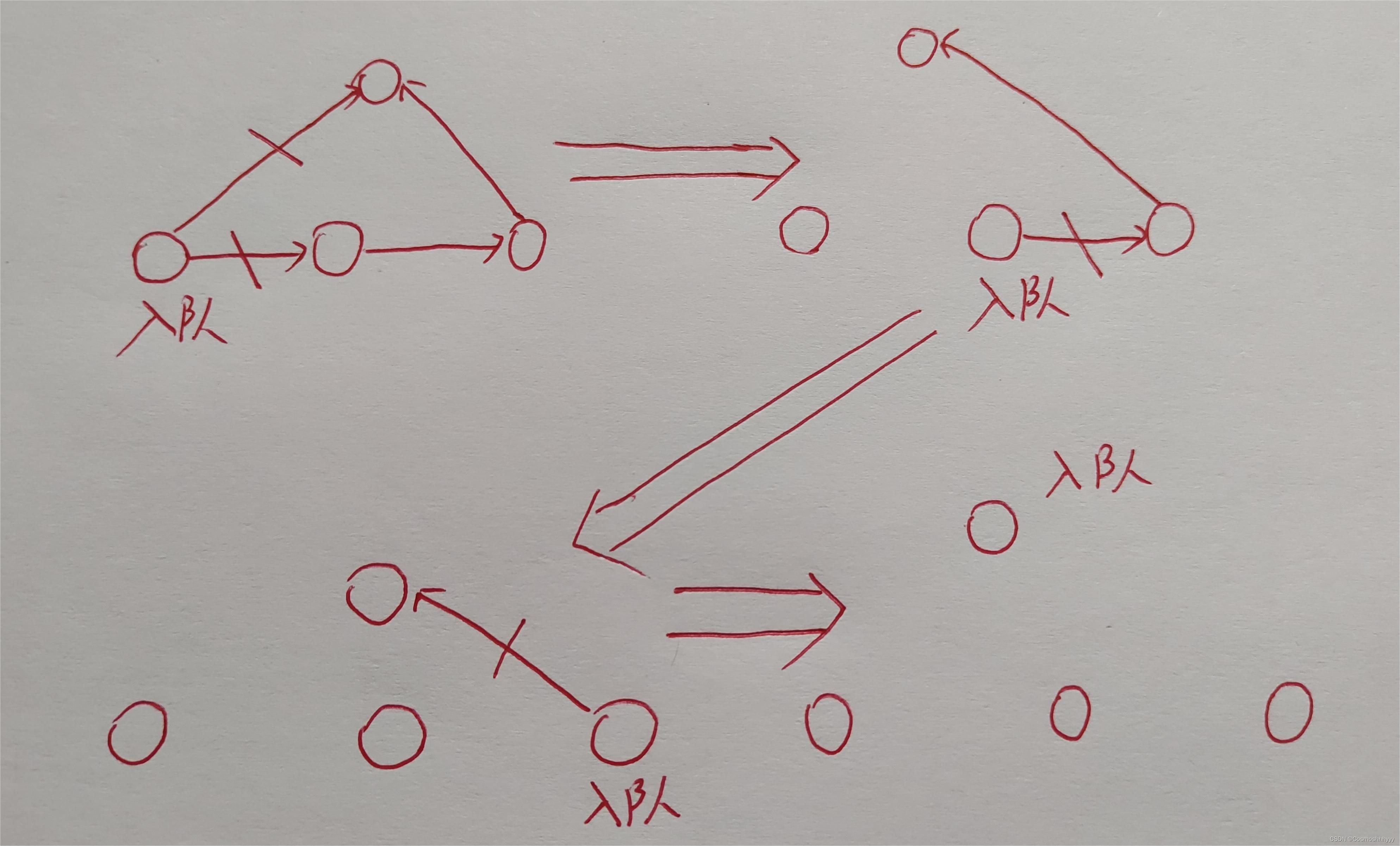
        拓扑排序（Topological Sorting）是一种针对有向无环图（DAG）的节点进行排序的算法。DAG是一个图，其中所有边都是有向的，并且不存在任何环路（即没有循环）。拓扑排序可以将这种图中的节点线性排序，使得所有的有向边从排在前面的节点指向排在后面的节点。

实现原理：

1. 找到入度为0的节点：入度是指有向图中指向某个节点的边的数量。在开始排序之前，首先找到所有入度为0的节点。这些节点是图中没有其他节点指向它们的节点，因此它们可以作为排序的起点。

2. 从图中删除入度为0的节点：将入度为0的节点从图中删除，并将与这些节点相连的边去掉，即将这些相连节点的入度减1。

3. 重复上述步骤：重复执行步骤1和步骤2，直到所有节点都被删除。每次找到入度为0的节点，并删除它们，直到没有节点剩余为止。

4. 排序结果：排序完成后，被删除的节点按照删除的顺序，从头到尾组成了一个拓扑排序序列。

        拓扑排序的结果不是唯一的，因为可能存在多个入度为0的节点。在实际应用中，如果图中存在环路（非DAG），则无法进行拓扑排序，因为无法满足拓扑排序的条件。

简答来说：

        其实就是简单的bfs，但是拓扑排序中每次都要以入度为0的结点开始bfs，所以相较于普通的bfs多了一个记录每个结点入度的d[N]数组，然后每次将删除边后，读入为0的结点入队。

        入队的结点顺序，就是拓扑排序的结果，我们用top[N]数组来记录。若最后入队过的结点小于总结点数，说明有环，返回false，可以判断此图是否可以拓扑排序。

例子

模板（C++）

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;

const int N = 100010;
int h[N], e[N], ne[N], idx; // 邻接表
int d[N], top[N]; // 每个节点入度，排序结果
int cnt = 0; // 记录top数组末尾位置
int n, m; // 结点个数，边数

// 邻接表连边方法
void add(int a, int b)
{
    e[idx] = b; ne[idx] = h[a]; h[a] = idx++;
}

// 拓扑排序
bool topsort()
{
    queue<int> q; // 队列
    
    for (int i = 1; i <= n; i++)
        if (d[i] == 0) q.push(i); // 入度为 0的入队
        
    while(q.size())
    {
        int t = q.front();
        top[cnt++] = t; // 记录入队顺序
        q.pop();
        // bfs
        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            d[j]--; // 此节点入度减一
            if(d[j] == 0) q.push(j); // 若入度减为0，入队
        }
    }
    if (cnt < n) return 0; // 入队的结点小于总结点数
    else return 1;
    
}

int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h); // 初始化表头
    // 建图
    while(m--)
    {
        int x, y; 
        cin >> x >> y;
        add(x, y);
        d[y] ++; // 入度++
    }
    if (topsort() == 0) cout << "-1"; // 若不能排序，输出-1
    else
    {
         for (int i = 0; i < n; i++)  cout << top[i] <<" "; // 输出排序结果
    }
    
    return 0;
}