前缀和
前缀和:一段序列里的前n项和
给出n个数,在给出q次问询,每次问询给出L、R,快速求出每组数组中一段L至R区间的和
给出一段数组,每次问询为求出l到r区间的和
普通方法:L到R进行遍历,那么在每次求区间和的过程中时间复杂度为O(n),q次问询时间复杂度为O(q*n)
前缀和:建立前缀和数组,sum[i]=sum[i-1]+arr[i]。(i-1存在越界的问题,所以i从1开始遍历)
计算L到R的区间和,包括arr[L]和arr[R]两个值(边界值),区间和=arr[R]-arr[L-1]
时间复杂度从O(q*n)降至O(q*1)
二维前缀和
二维前缀和数组是原数组它本身位置的数及其左上角全部的数
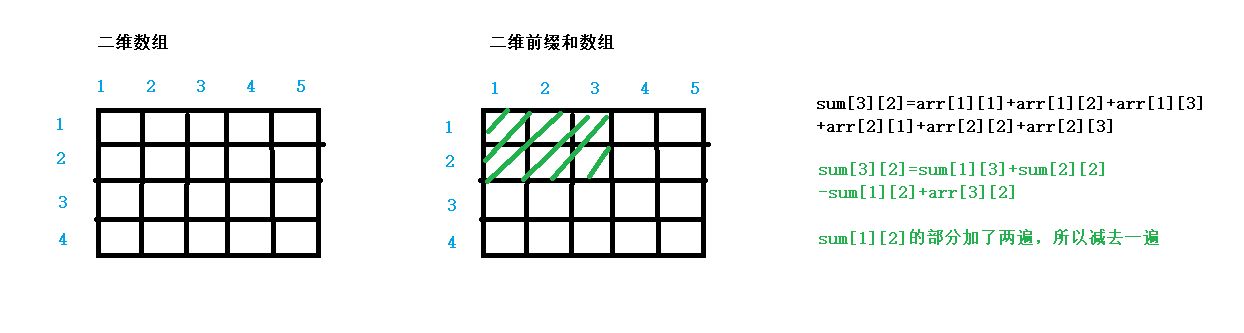
二维前缀和的应用:求二维数组中arr[x1][y1]到arr[x2][y2]区间内的数之和
差分
给出n个数,再给出q次问询,每次问询给出L、R、X,要求在L到R上每一个值都加上X,直到最后输出这个数组
普通方法:遍历,时间复杂度为O(q*n)
差分:建立差分数组,difference[i]=arr[i]-arr[i-1],arr[i]=difference[i]+arr[i-1]。
(同样i从1开始遍历)
时间复杂度从O(q*n)降至O(q*1)
数组arr
| 1 | 1 | 1 | 1 | 1 | 1 |
差分数组difference
| 1 | 0 | 0 | 0 | 0 | 0 |
此时,L=2,R=4,X=1
操作方式:difference[L]=difference[L]+X,影响L之后的数字
difference[R+1]=difference[R+1]-X,避免影响R+1以及之后的数字
操作后的差分数组difference
| 1 | 1 | 0 | 0 | -1 | 0 |
还原后的数组arr
| 1 | 2 | 2 | 2 | 1 | 1 |
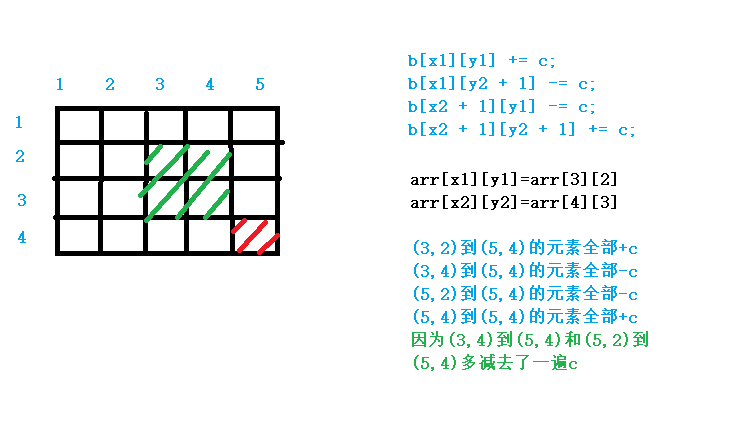
二维差分
一维差分修改差分数组中的某个数,影响的是原数组它本身及其之后的数
二维差分修改差分数组中的某个数,影响的是原数组它本身及其右下角全部的数
二维差分的应用:对以 x1, y1 为左上角, x2, y2 为右下角的矩阵插入一个值 / 修改值