二叉搜索树(Binary Search Tree)
特性
任意一个节点的所有左子树都比它小,所有右子树都比它大;
复杂度
当我们查找某个节点的时候,先从根节点开始比较,如果比根节点大走右子树,如果比根节点小走左子树。可以看到查询的复杂度呢,是完全依赖于树的深度。 写入某个节点的时候同理; 所以二叉搜索树的读和写的复杂度都是 O(log n)。search O(log n)。
缺点
当我们插入连续自增和自减的数据时,它就会变成一条连续的左子树或者连续的右子树。从而树型结构变成了线性结构。线性结构的复杂度依赖的还是树的深度,查询和插入复杂度从原来树型结构O(log n)变成了O(n)。BST表现性能会退化,一般常见的语言中,使用的存储结构会发现正真使用原生的BST的会非常少,都是经过一些优化的数据结构。
平衡二叉树(AVL)
全称为“平衡二叉搜索树”,它是由苏联数学家Adelson-Velsky 和 Landis 提出来的,因此平衡二叉树又叫AVL树。
特性
任意节点的左子树和右子树的深度差 <= 1,条件是比较苛刻的,自平衡和优化也需要浪费一些时间;
复杂度
查询、读和写的复杂度都是 O(log n),是继承至 BST 算比较好的优化;
红黑树(Red Black Tree)
特性
有人说红黑树也是自平衡二叉树的一种,不过对于“平衡”的标准比自平衡二叉树来说要严格的多。
- 红黑代表某个节点要么是红节点,否则就是黑节点。
- root节点是个黑节点。
- 叶子节点是黑节点,也可以是 null 节点,所以 null 节点 也是黑节点 。
- 红节点的子节点必须是黑节点。
从以上4个特性可以看到,红节点生存非常恶劣。
- 新插入节点是红节点,但是可能会经过红黑的自平衡和优化变成黑节点。
- 任意节点到叶子结点路径上黑节点的个数相同。上界:路径上黑节点个数相同(n)。下界:关注红节点出现的苛刻条件,节点数差一倍(2n)。
红黑树一系列特性要实现的终极效果:左右子树的深度差一倍以内,相较于AVL来说条件会宽松很多。所以插入节点时的变化要少很多。写的性能会高很多。
面试题
Java8中HashMap实现,每一个桶是一个链表,当链表长度达到8以上了,那么这个链表就会变成红黑树,为什么要选择红黑树的这种存储结构,而不是 BST 或 AVL,题目也可以改成:TreeMap 底层是红黑树而非 BST 或 AVL。
- 当我们插入连续自增和自减的数据时,它就会变成一条连续的左子树或者连续的右子树。从而树型结构变成了线性结构,从而退化成链表。
- 红黑树相比于 AVL 树,它心目中的“平衡”条件是更加宽松的,使得在节点插入的时候,整颗树的变动会小很多。那么红黑树的复杂度也是 O(log n)?我们知道树的复杂度依赖于树的深度。
复杂度
n个节点 = Nr(n个红节点) + Nb(n个黑节点),当我遮住红节点时,它就是一颗 AVL 树。当显露出红节点时,任意节点到叶子结点,最复杂的结构就是红黑相间,节点数相差一倍。最差情况复杂度为 O(2 x log Nb) = O(2 x log n),Nb = n。常量 2 可以约掉,最后红黑树的复杂度时 O(log n)。
插入流程
| 父节点 | 叔节点 | 类型 | 操作 |
|---|---|---|---|
| 黑 | 无需操作 | ||
| 红 | 红 | 父节点和叔节点都变黑,祖父变红。祖父变成当前节点,递归这个规则。 | |
| 红 | 黑 | 左左 | 右旋 + 变色 |
| 红 | 黑 | 右右 | 左旋 + 变色 |
| 红 | 黑 | 左右 | 先左旋,再右旋 + 变色 |
| 红 | 黑 | 右左 | 先右旋,再左旋 + 变色 |
-
父节点比较好理解,就是当前节点的父节点。
-
叔节点,就是父节点同一层的兄弟节点。
插入 0001 根节点
插入节点都是红节点,而红黑树的特性根节点是黑节点,红节点直接变成黑节点就可以了。
0001根节点
插入 0002 子节点
遵循 BST 的特性。父节点是根节点,叔节点是 null 节点,无需操作。
0002节点
插入 0003 节点
父节点 0002 是红节点,叔节点 null 节点是 0001 节点的左子节点, 等价于黑节点。父叔节点满足:红黑。
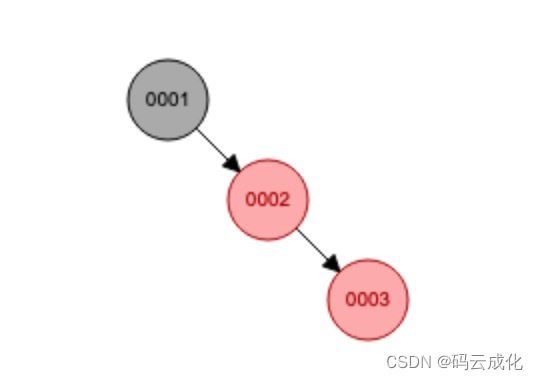
0003节点
类型是:右右,也就是祖父节点的右右节点。左旋:祖父节点变为父节点的左子节点,父亲与祖父辈分颠倒。
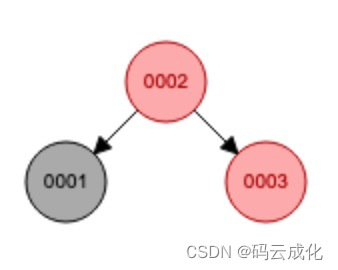
0003节点,左旋
变色:父节点是根节点,红色显然是不行的,遵循红黑树特性。根节点(任意节点)至叶子节点路径中黑节点个数相同,父节点和祖父节点发生颜色变化,红变黑,黑变红。
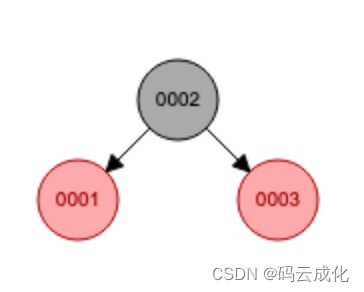
0003节点,变色
插入 0004 节点
父节点 0003 是红节点,叔节点 0001 是红节点,父叔节点满足:红红,类型:无。

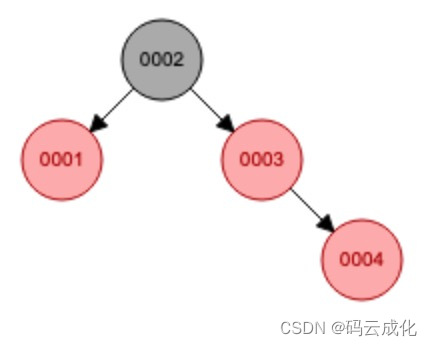
0004节点
父叔节点都变黑,祖父变红。
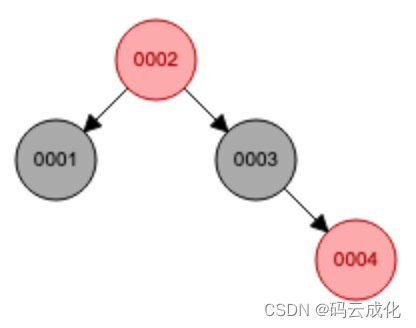
0004节点,变色
祖父节点变成当前插入的节点,递归父叔节点都是红节点的规则。遵循红黑树特性,祖父节点是根节点必须为黑节点,变色为黑节点。
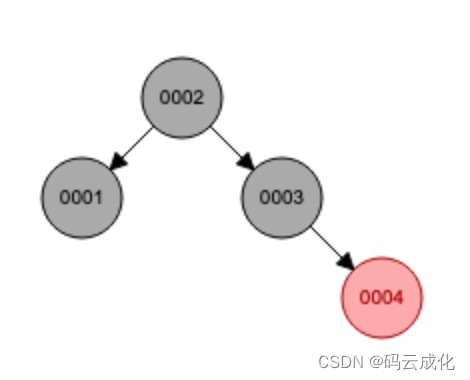
0004节点,变色
插入 0010 节点
父叔:红黑,类型:右右,祖父节点的右右节点(没有叔节点)。
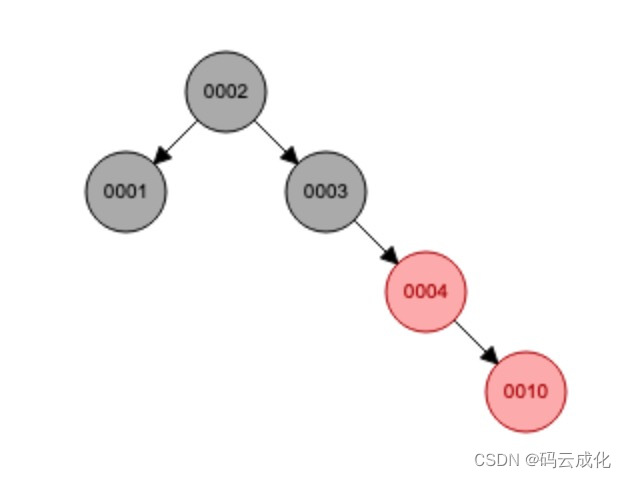
0010节点
先左旋。
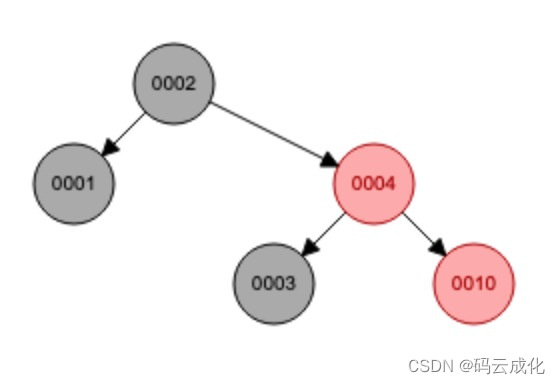
0010节点,左旋
后变色,遵循红黑树特性,父节点(任意节点)至叶子节点路径中黑色节点个数相同,父节点和祖父节点发生颜色变化,红变黑,黑变红。
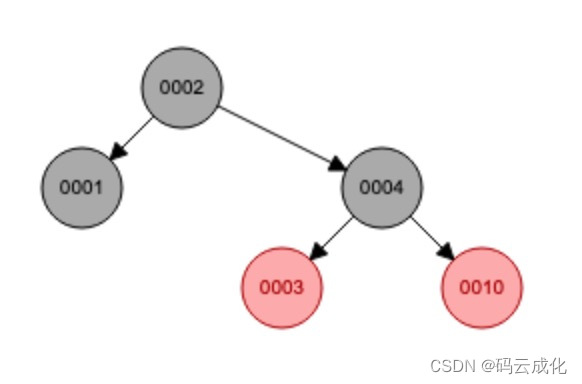
0010节点,变色
插入 0015 节点
类型:红红。
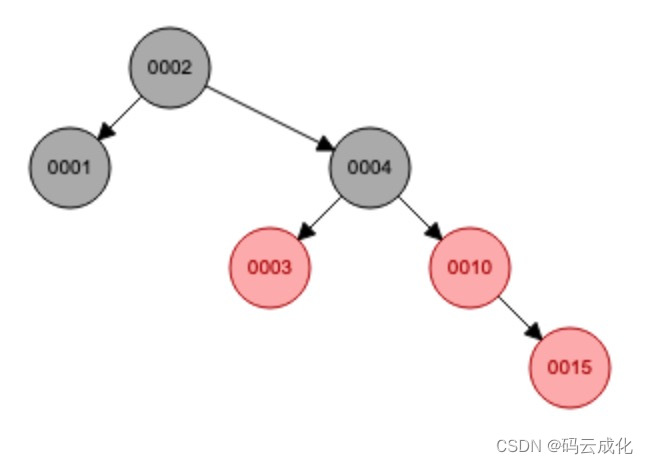
0015节点
变色:父叔节点变黑,祖父节点变红。祖父节点作为当前节点,继续递归类型:红红规则。

0015节点,变色
插入 0012 节点
遵循 BST 特性。 类型:右左,祖父节点的右左节点。
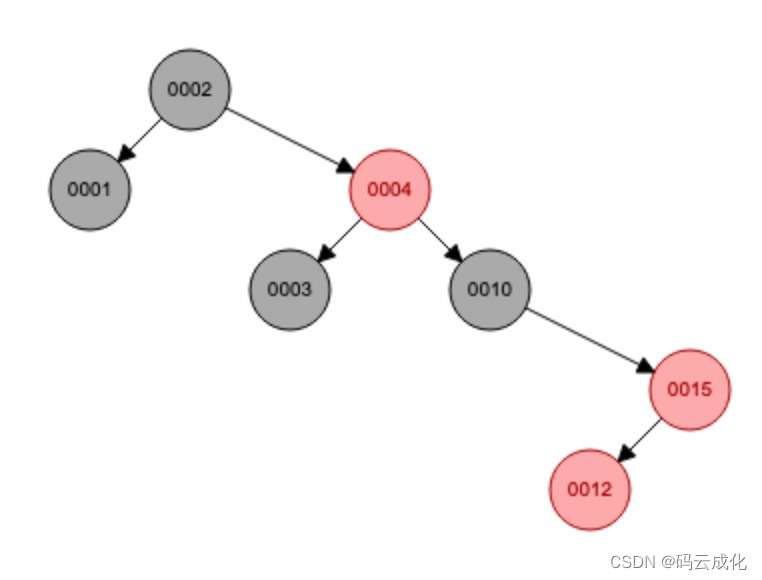
0012节点
先右旋:当前节点变为父节点,父节点变为右子节点,父子颠倒。
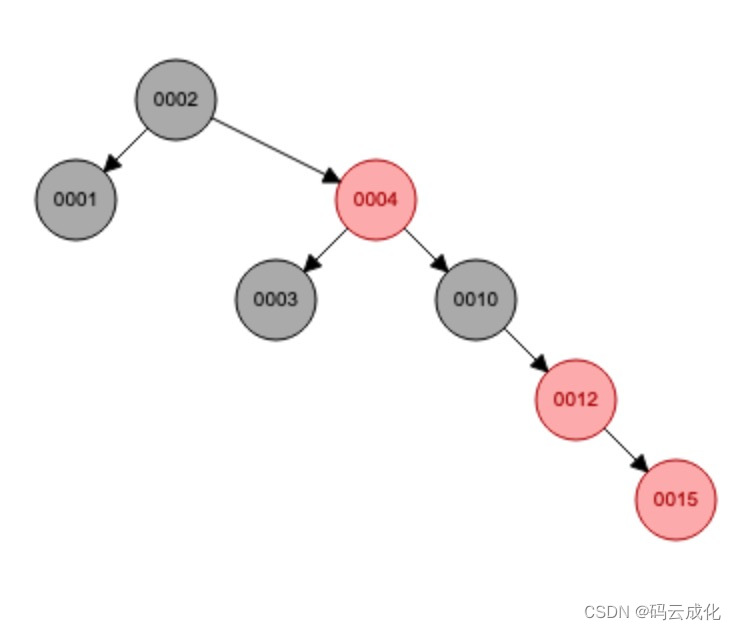
0012节点,右旋
再左旋 + 变色。
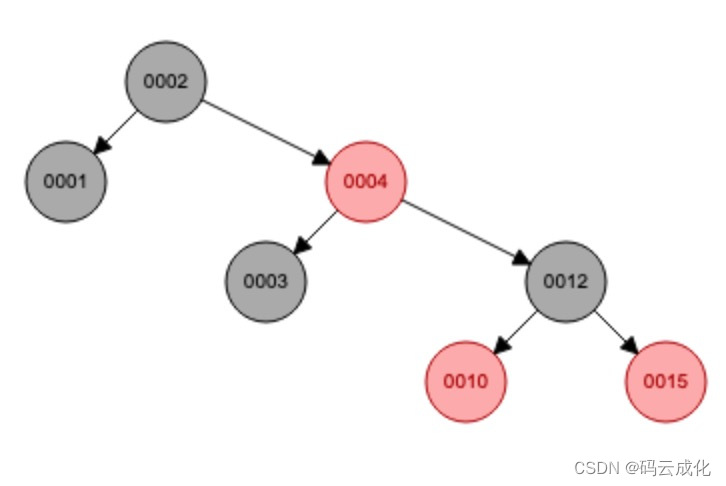
0012节点,左旋 + 变色
微信公众号:码云成化
关注可了解更多的教程及排版技巧。问题或建议,请公众号留言;
如果你觉得阿云对你有帮助,欢迎赞赏
希望可以帮到你!相互取暖,共同进步。