一、SPFA算法回顾：

我们在第18章中利用dijkstra算法推导出了SPFA算法，如果大家没有看过上一篇文章的话，建议大家先去看作者是如何推导出SPFA算法的，再来看本章节。
传送门：第十八章 SPFA算法以及负环问题

那么今天的Bllman-Ford算法其实就是暴力版本的SPFA

二、Bellman-Ford算法

1、算法推导：

在SPFA算法中，我们利用了队列。另外，我们还使用了一个st数组，这个数组的作用就是标记当前点是否在队里，如果不在队里，我让他入队，如果在队里，我不让它入队。我们通过控制点的入队来避免重复的松弛。那么假设你不明白，那我不管三七二十一，我就让点入队，不管别的，反正最后的结果也只是多重复了几遍，但是结果依旧是正确的。

那么我们在这里思考一下，我们的点最多入队多少次呢？

一个点入队，说明这个点被松弛成功了一次，换句话说我们想知道一个点最多入队多少次，其实就是想知道我们求出一个最短路最多成功松弛多少次。
我们看下面的式子：
在这里插入图片描述

我们知道n个点的最短路，最多含有n-1条边。
假设我们想完成松弛：d[n]<d[n-1]+w，那么我就得先知道d[n-1]，想知道d[n-1]，就得知道d[n-2]…以此类推。我们发现，我们最多需要松弛n-1次。也就是说，我们的每个点最多入队n-1次。

那么既然这样的话，我们根本没必要去用队列了。直接写一个循环就好了。

1、算法模板：

void Bellman-Ford()
{
	memset(dist, 0x3f, sizeof dist);
	dis[1]=0;
	for(int i=0;i<n-1;i++)
	{
		for(int x=1;<=n;x++)
		{
			for(int y=h[x];y!=-1;y++)
			{
				if(dis[y]>dis[x]+w[y])
				{
					dis[y]=dis[x]+w[y];
				}
			}
		}
	}
}

在这里插入图片描述

以上就是邻接表版本的Bellman-Ford算法。
但是这个代码在形式上，还是有点复杂的。那么我们如何在形式上进行简化呢？我们看下面这个图。
在这里插入图片描述

将最里面的两层循环放在一起看的话，我们发现其实就是访问了每一条边。因此，我们创建一个结构体数组，这个数组存储所有的边。

const int N = 510, M = 10010;
int n, m;
int dist[N];

struct Edge
{
    int a, b, c;
}edges[M];

void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for (int i = 0; i < n-1; i ++ )
    {
        for (int j = 0; j < m; j ++ )
        {
            auto e = edges[j];
            dist[e.b] = min(dist[e.b], dist[e.a] + e.c);
        }
    }
}

在这里插入图片描述
我们发现，在最坏情况下，我们循环n-1次，也能找到边数为n-1的最短路（如果存在这样的最短路。）。那么我们延申一下，如果我们循环1次，那么在最坏情况下，我们也能得到边数为1的最短路。

所以，最外层的循环中，我们循环k次的含义就是，我们在最坏情况下也能找到边数为k-1的最短路。

因此，我们看下面这道题：

三、例题：

1、问题：

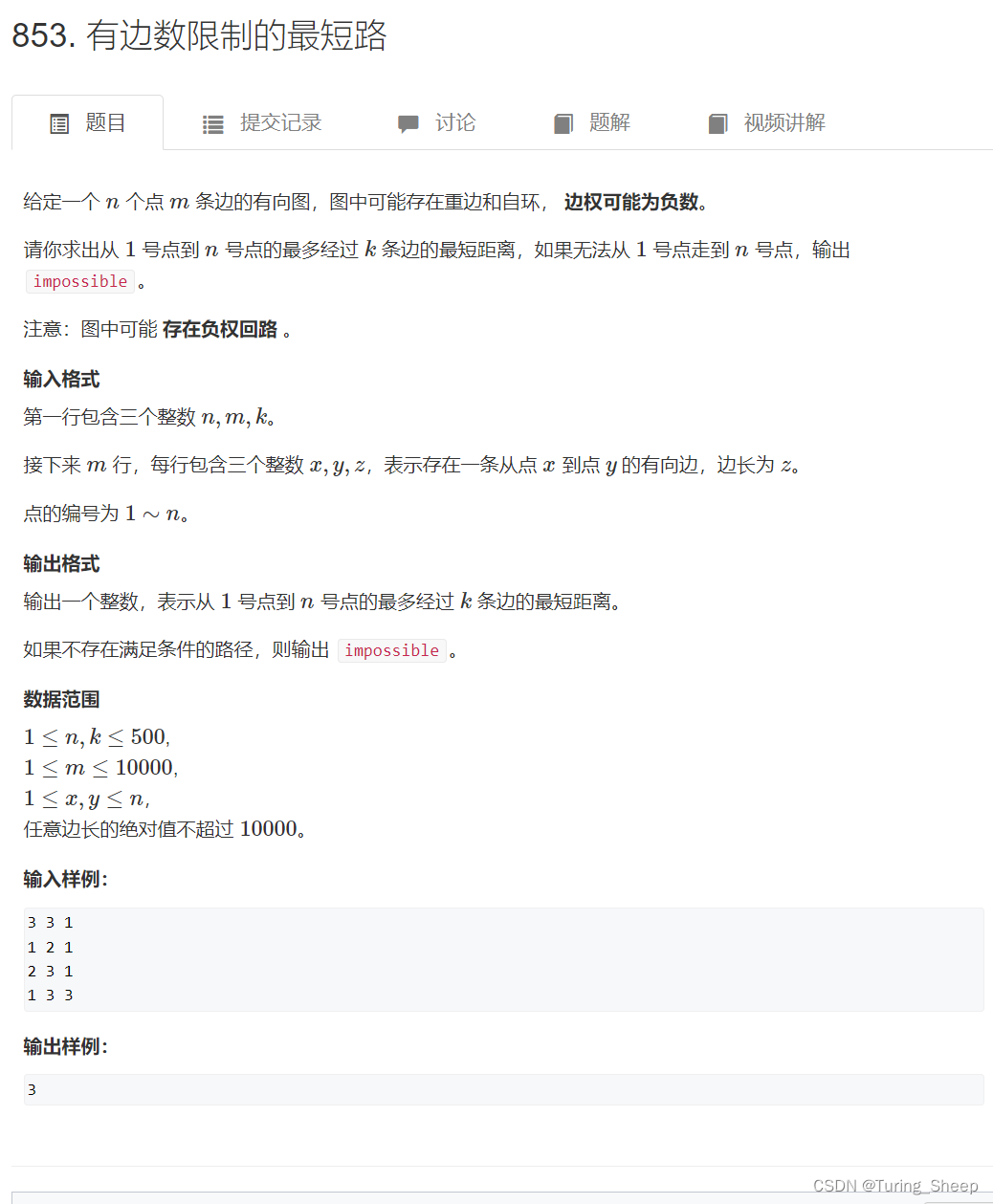
在这里插入图片描述
当遇到这种有边数限制的最短路问题的时候，我们要想到使用我们的BF算法。

那么我们将该算法的最外层循环设置为k次，那么我们就能保证，即使在最坏的情况下，我们也能找到所有边数小于等于k的最短路。
但是，我们也能找到部分大于等于k的最短路：
为什么呢？
我们看一下极端情况：
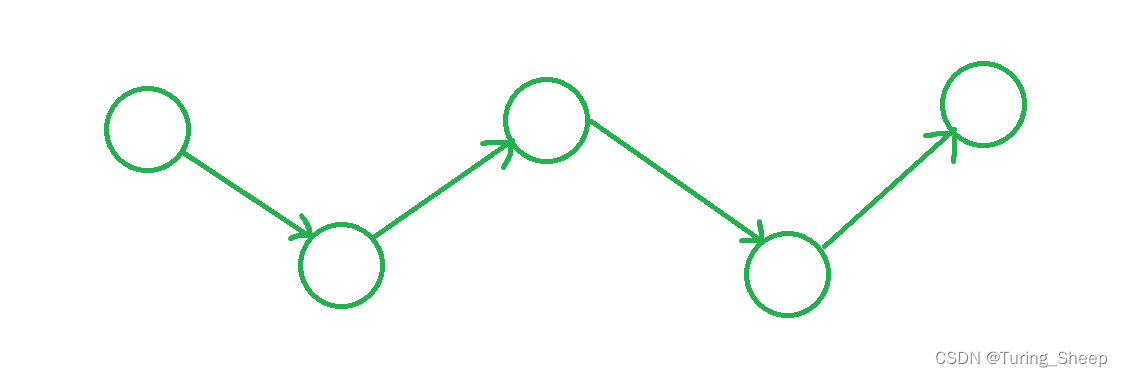
在这里插入图片描述

假设我们松弛边的顺序为：从右到左遍历。那么我在第一次循环中就能找到边数为n-1的最短路。
那么在最坏情况下：我们从左到右遍历，那么我在第一次循环中只能找到边数为1的最短路。

那么在这道题中，我们很明显要避免掉边数大于k的最短路。

那么怎么办呢？

我们还是以刚才的例子为例：

在最好的情况下，我们之所以能实现连锁反应，是因为我们的上一次成功了。但是如果我们不上一次的结果，那么它就不会成功。

因此，我们松弛本次的时候，只要使用上上次的松弛结果即可。

所以，我们需要加上一个备份的变量。

2、模板：

#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, M = 10010;
struct Edge
{
    int a, b, c;
}edges[M];
int n, m, k;
int dist[N];
int last[N];
void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for (int i = 0; i < k; i ++ )
    {
        memcpy(last, dist, sizeof dist);
        for (int j = 0; j < m; j ++ )
        {
            auto e = edges[j];
            dist[e.b] = min(dist[e.b], last[e.a] + e.c);
        }
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i < m; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        edges[i] = {a, b, c};
    }
    bellman_ford();
    if (dist[n] > 0x3f3f3f3f / 2) puts("impossible");
    else printf("%d\n", dist[n]);
    return 0;
}