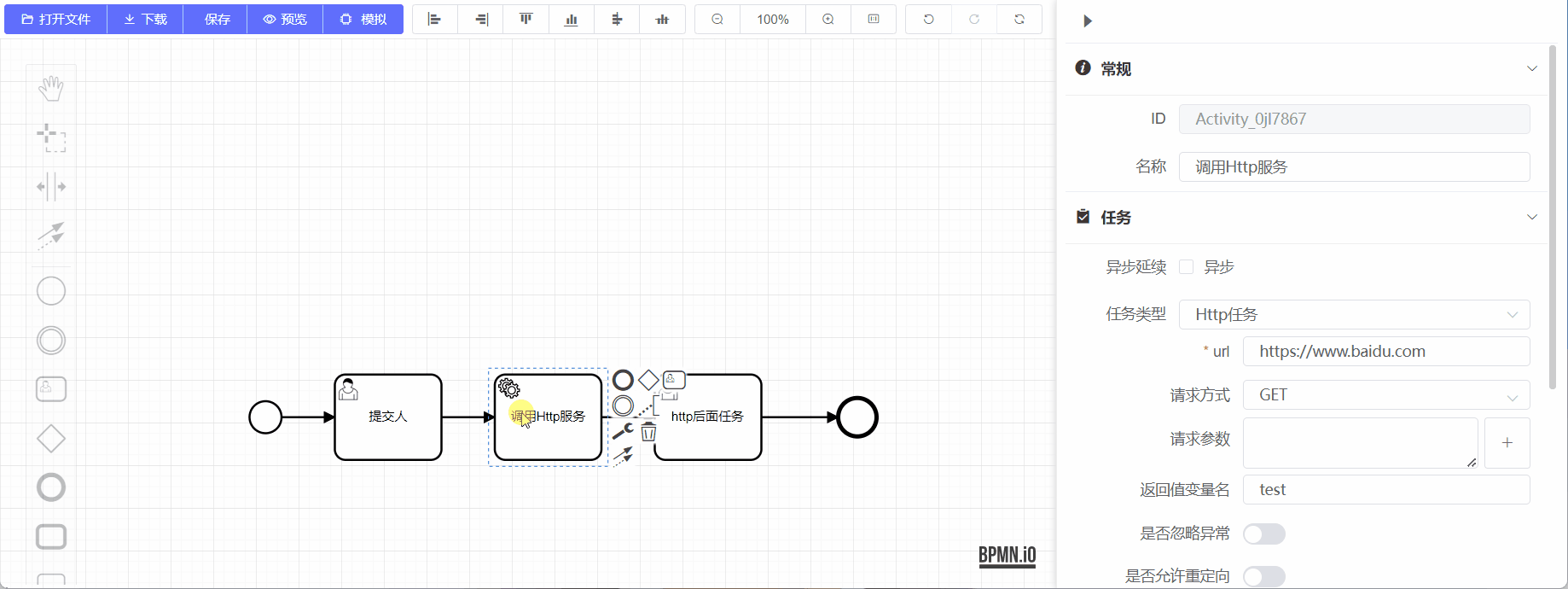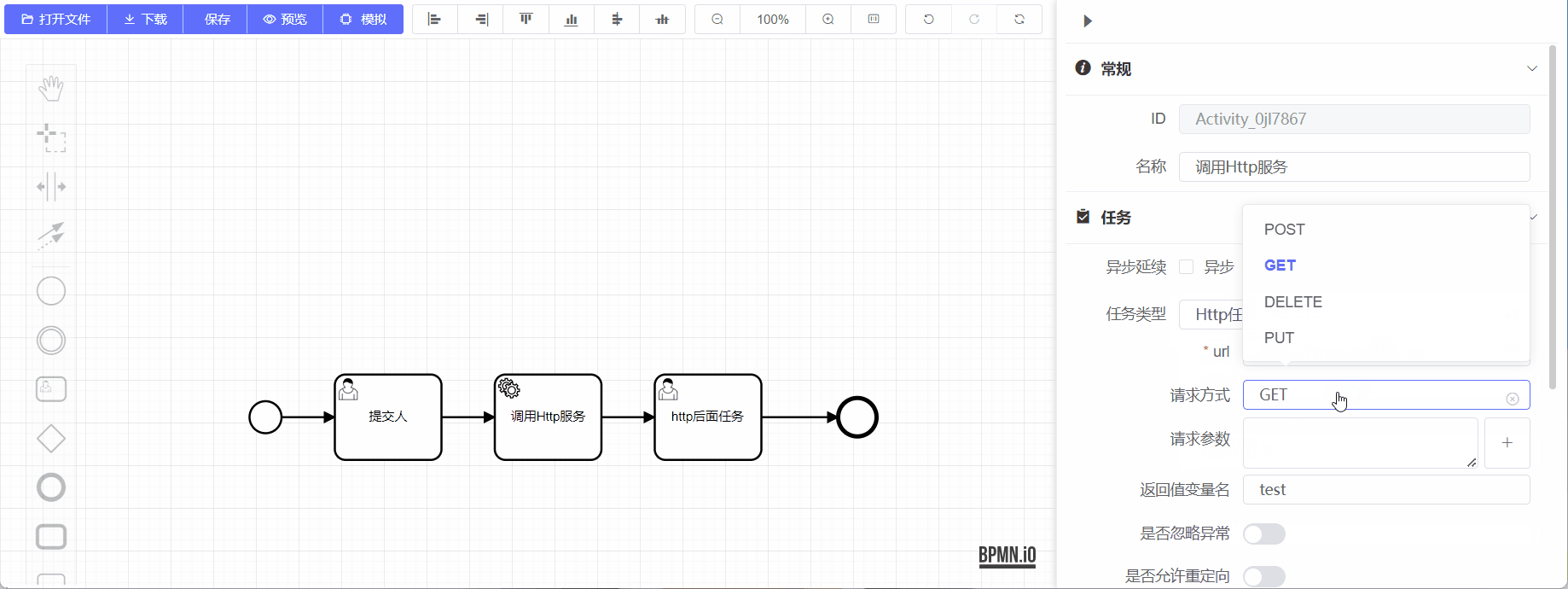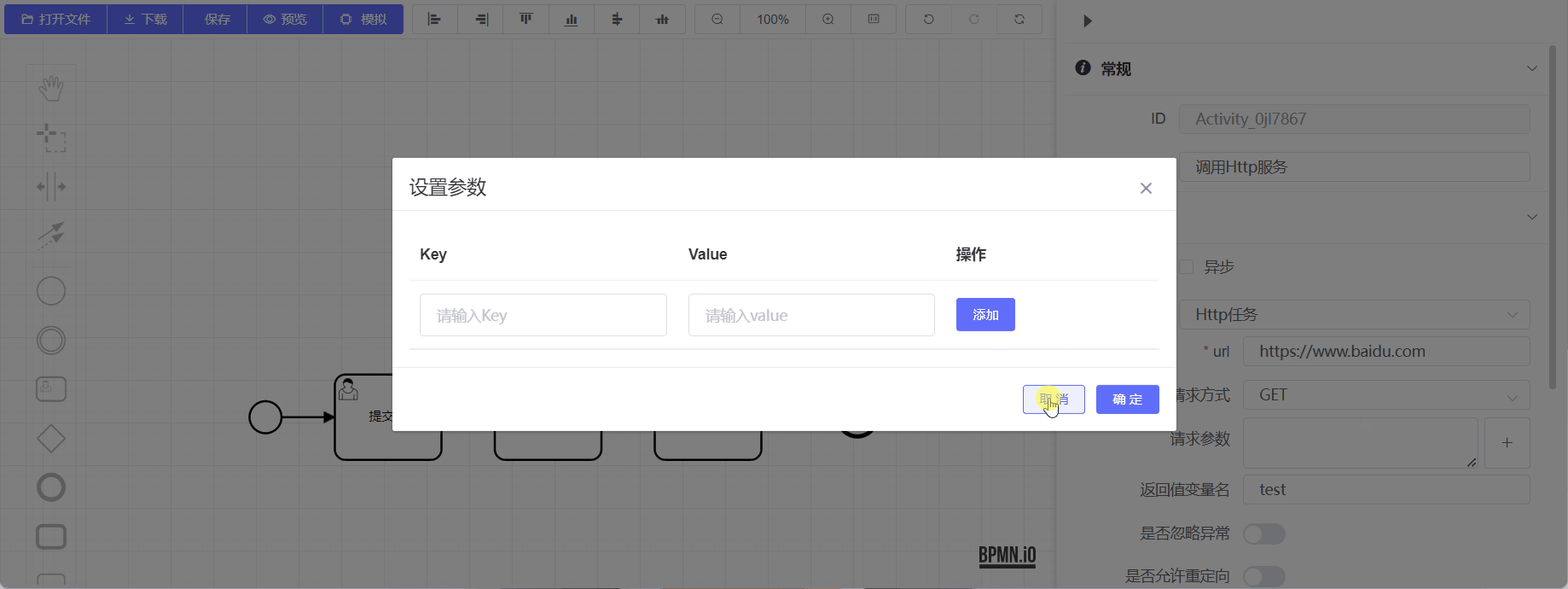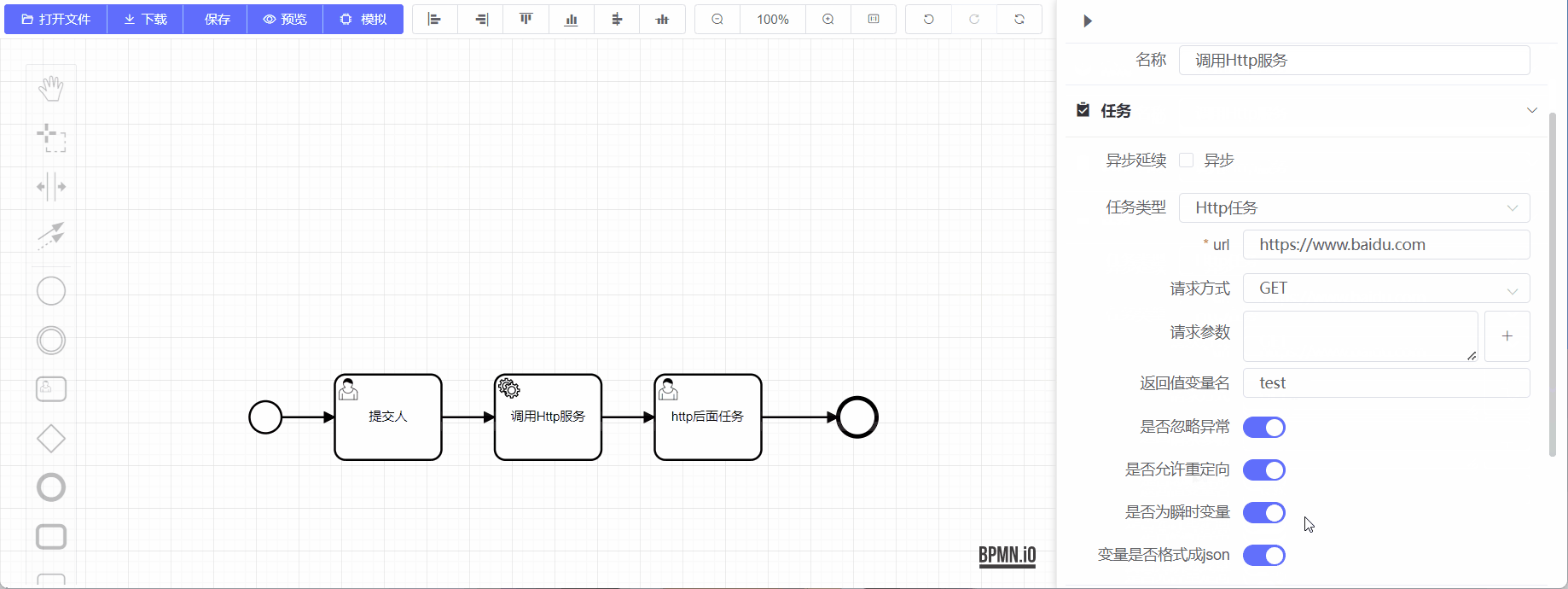
首先我们先说下网络编程API：

数据在网络上通信，通信的双方一个是 客户端， 一个是 服务器

更具体来说，不是 客户端和服务器这两个机器在  经由互联网   进行通信，

                       而是 客户端上的某一进程 与 服务器端的某一进程  进行通信。

因此，客户端与服务器间的通信  是  一个进程间通信，只不过通信的两个进程不在同一机器上。

所以进程间通信方式 实际上有 ①管道（命名管道、无名管道）；②消息队列；③共享内存；④信号量；⑤信号；⑥套接字Socket 这6种方式

其中的 套接字Socket 通信就是指 不在同一机器上，需要经由网络进行通信的 进程间通信方式

【具体详见： XXXXX插入一条链接】--》链接内容就是socket 作为内河中的缓冲区，是如何被fd指向来接受梁金成穿来穿去的数据的

---

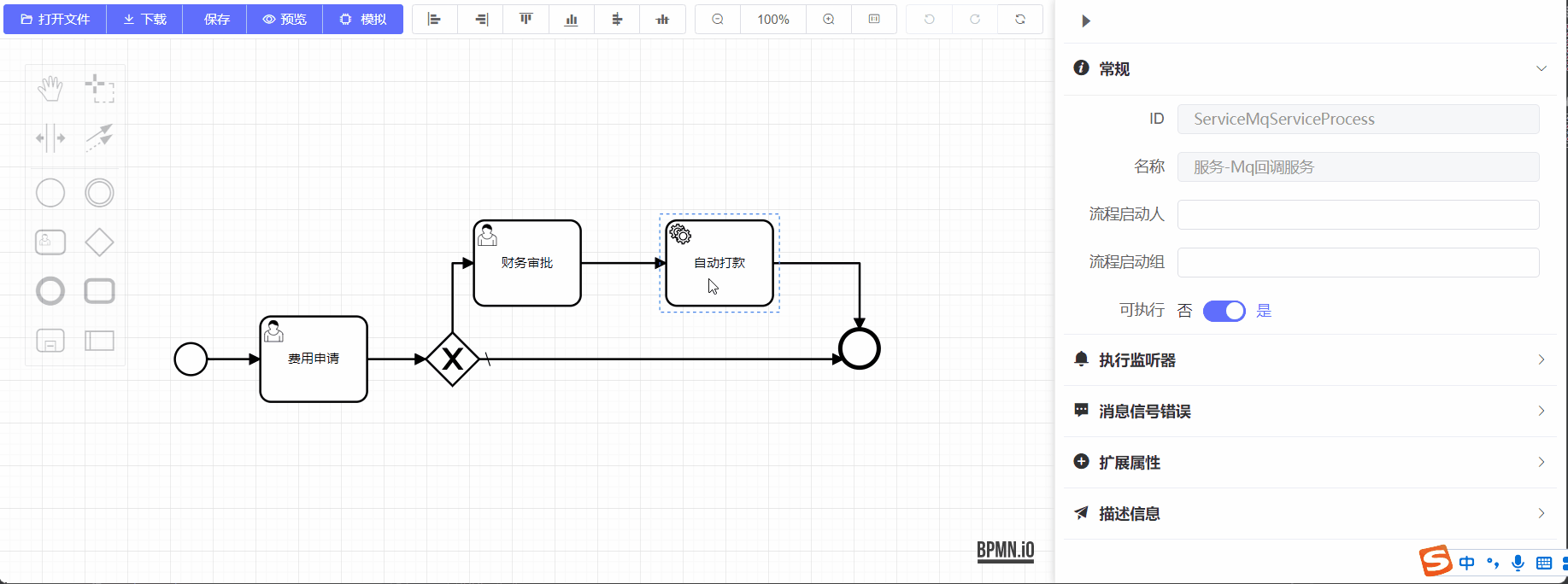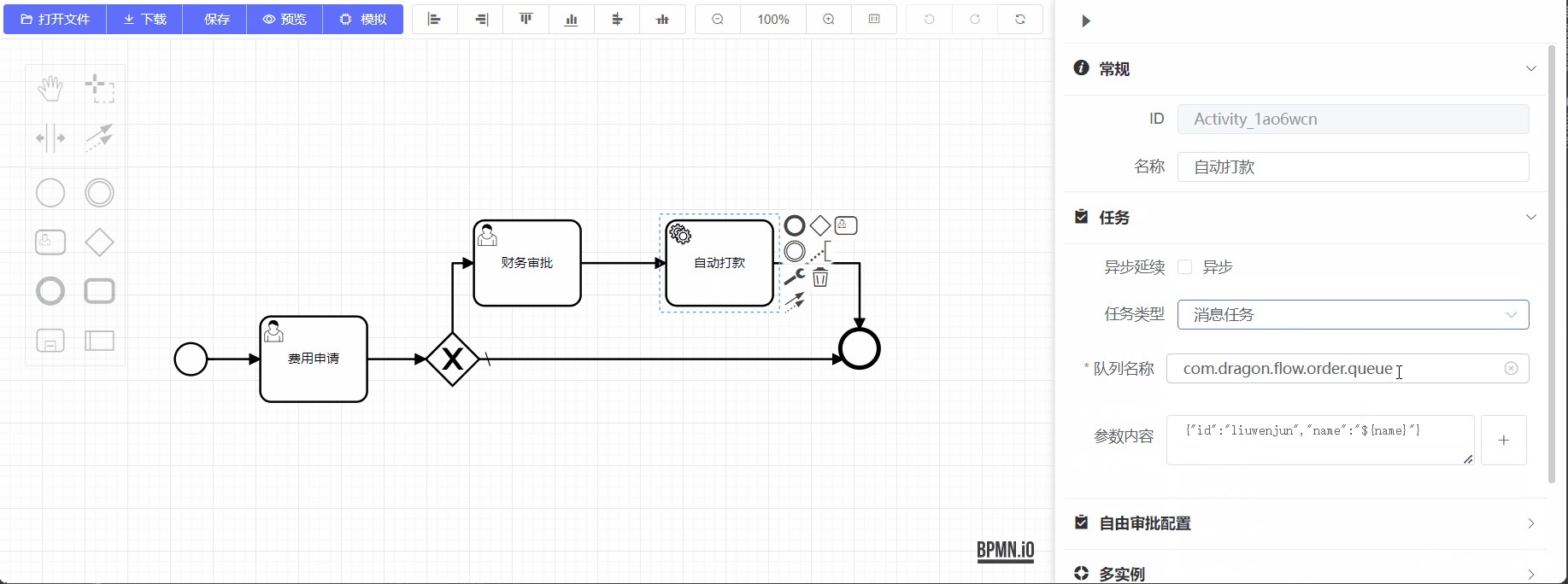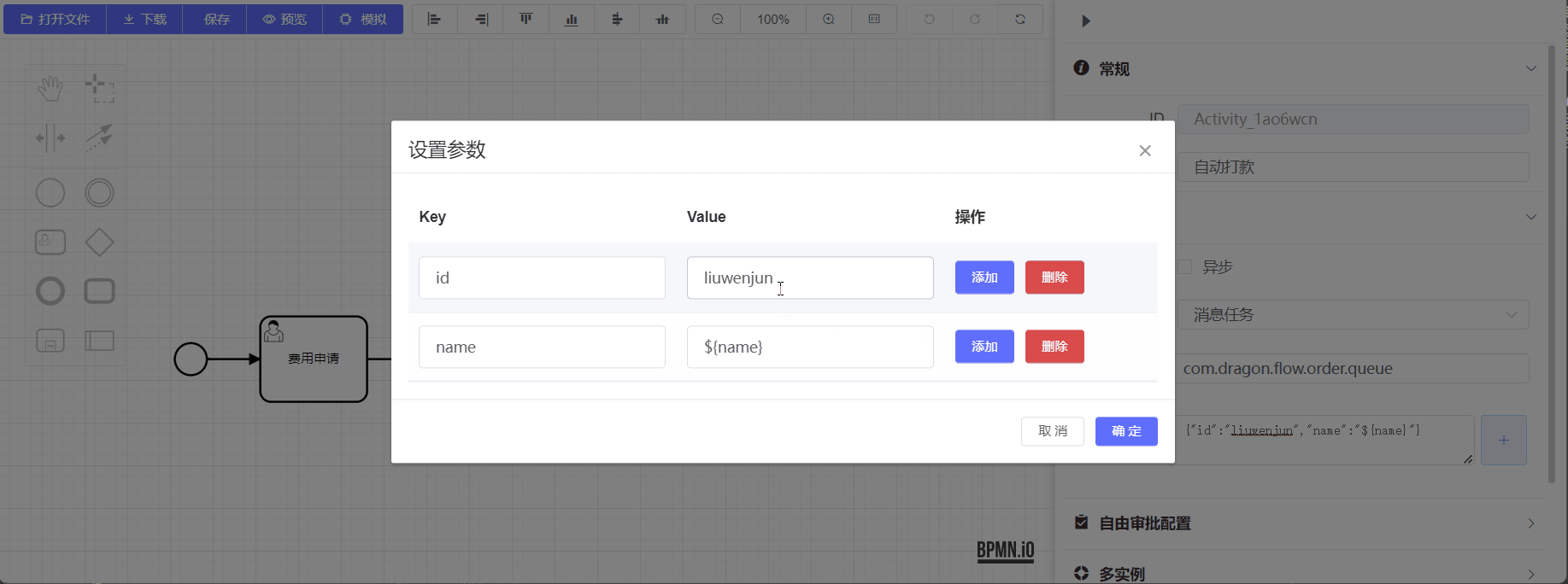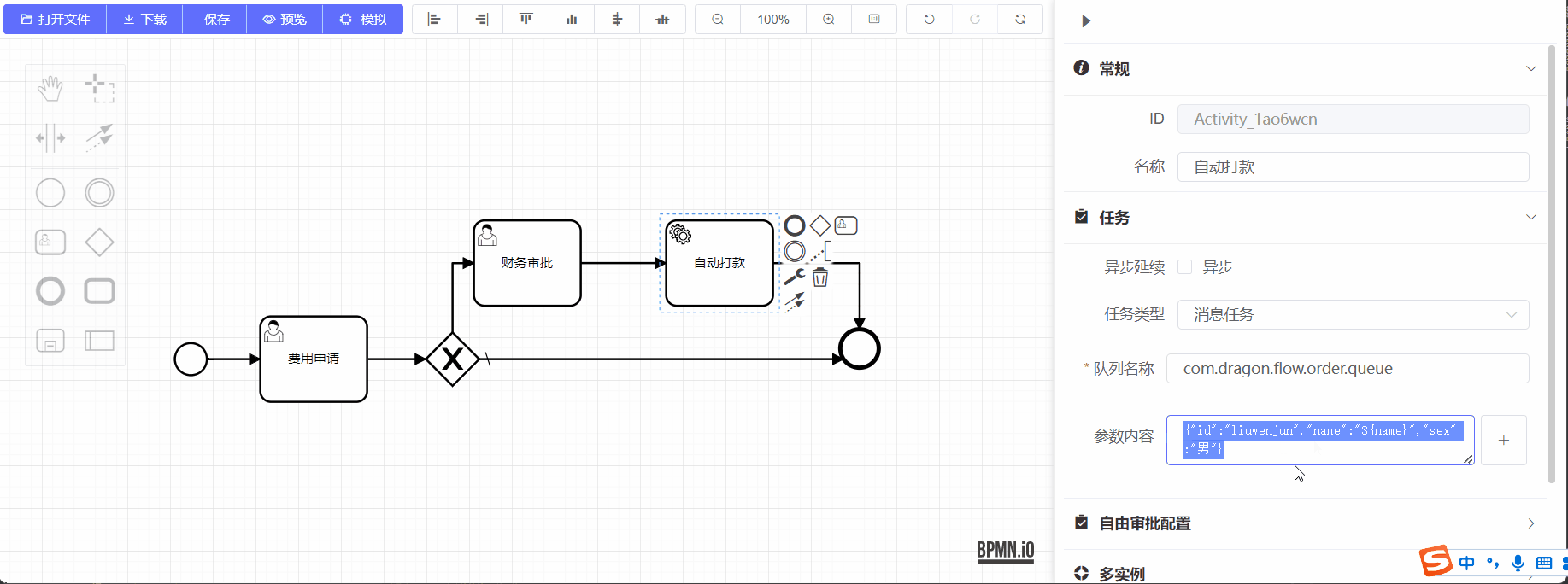
现在，客户端进程 与 服务器进程要通信，如何使用Socket套接字呢，需要以下流程：

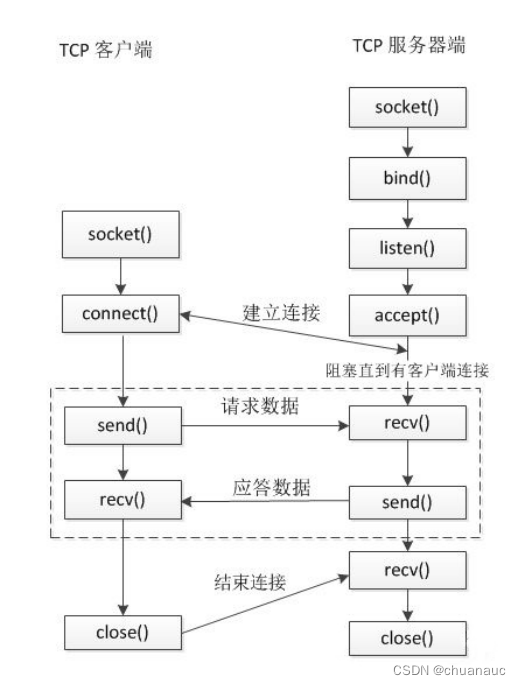
不加任何IO复用技术的客户端与服务器之间数据的交换调用函数如下：

 使用epoll来监听的socket通信流程调用API如下：（图中只画了三次握手和传输数据，没画关闭连接阶段，，，）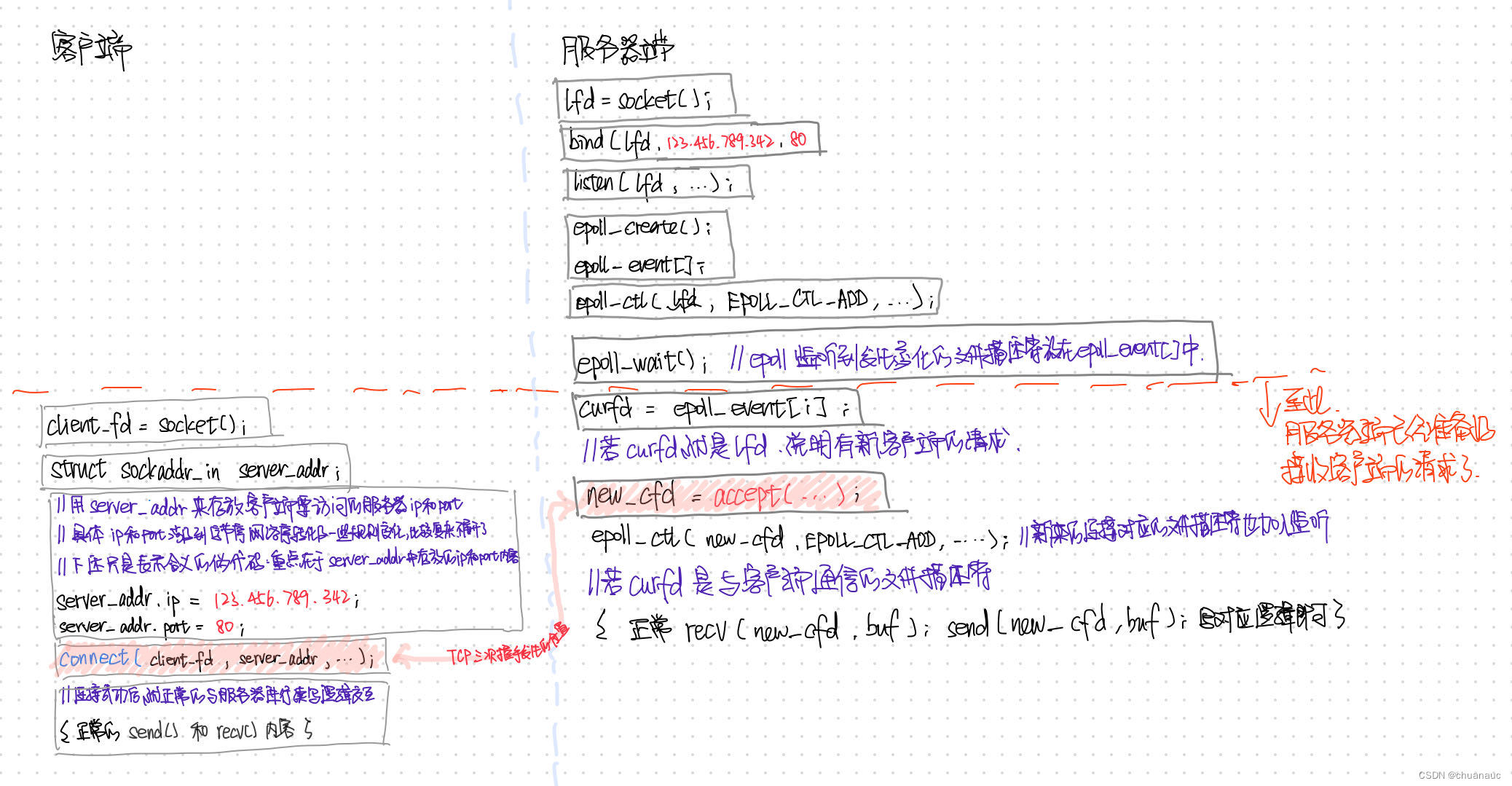

 但，无论是哪种方式（无论是程序员自己写逻辑轮询监听文件描述符还是使用select\poll\epoll），客户端与服务器间建立连接【发生三次握手】的位置都是：connect()函数 与 accept()函数交互的位置，如下图所示：

 

---

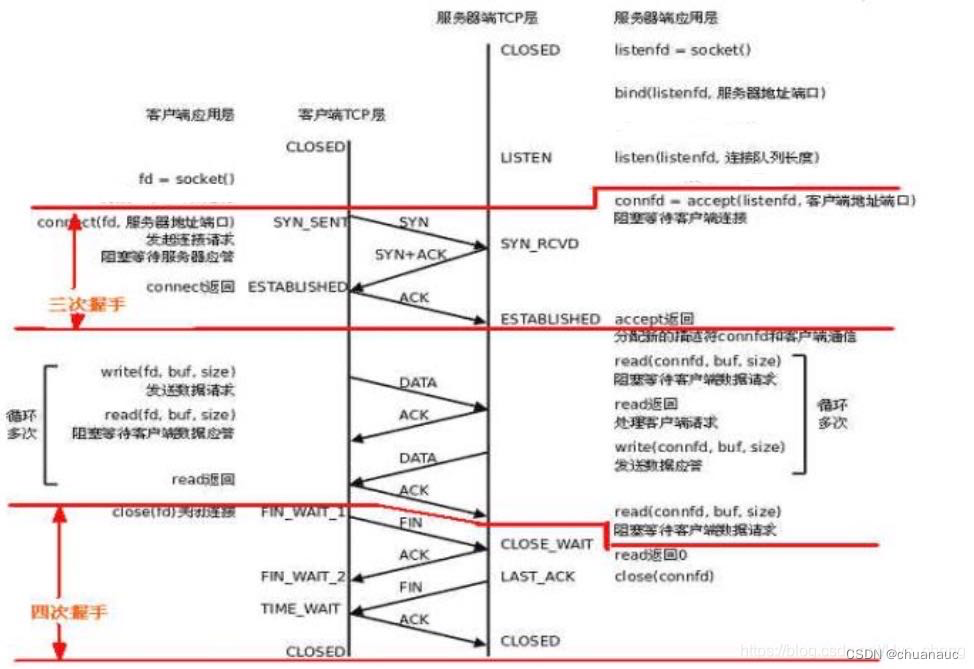
首先，让我们通过三次握手四次挥手过程的状态 来解释一下：

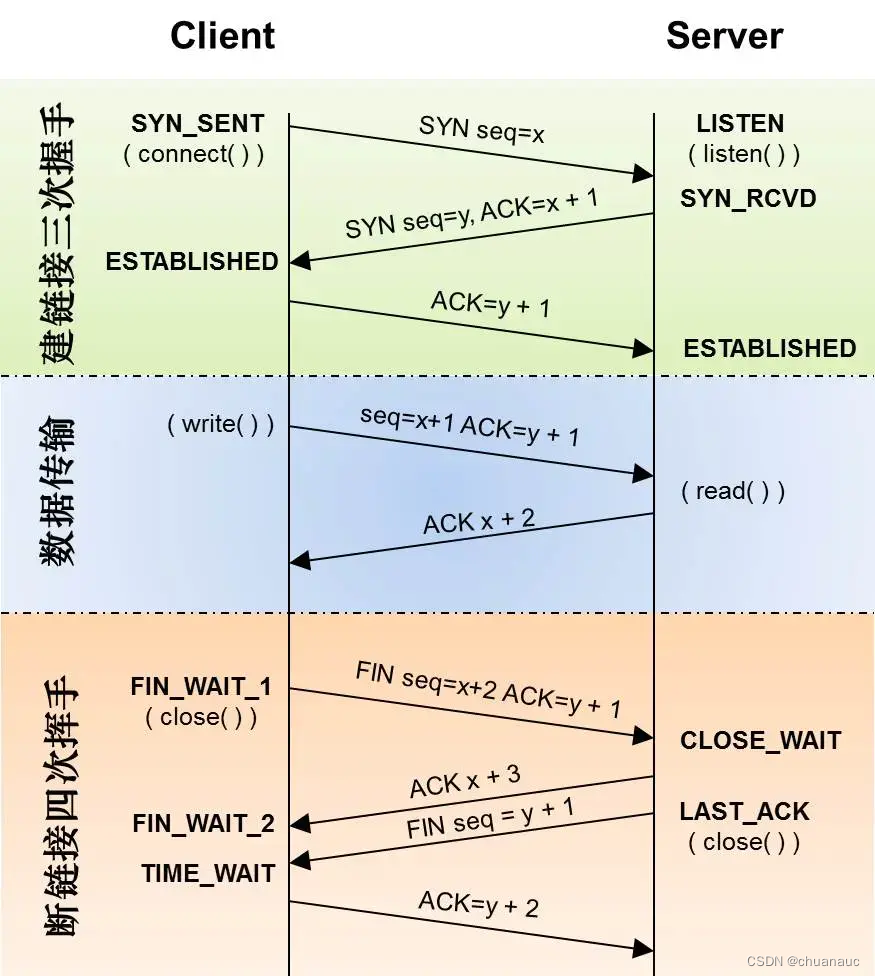
 连接建立阶段：

第一次握手：客户端的应用进程  向 服务器端 发出连接请求报文：发送连接请求后，客户端状态变为 "SYN_SENT"

请求报文内容为：其首部中：SYN值置为1 ；seq=x

第二次握手：服务器应用进程 响应 客户端的连接请求，向客户端发回 确认报文和连接请求 ： 而后，服务器端的状态变为 "SYN_RECV"

请求报文内容为：其首部中：SYN值置为1，ACK值置为1 ；ack=x+1，seq=y。

第三次握手：客户端收到确认报文之后，通知上层应用进程连接已建立，并向服务器发出确认报文：而后，客户端状态变为 "ESTABLISHED"

请求报文内容为：其首部中：ACK值置为1，ack=y+1

(服务器端 收到 第三次握手客户端发来的确认报文，状态也变为 "ESTABLISHED")

至此，TCP连接就建立了，客户端和服务器可以愉快地玩耍了。只要通信双方没有一方发出连接释放的请求，连接就将一直保持。
 

 连接释放阶段：（假设客户端主动关闭连接）

第一次挥手：客户端发送一个断开连接包（FIN包）：而后，客户端状态变为 "FIN_WAIT_1"

请求报文内容为：其首部中：FIN值置为1，ACK值置为1 ；ack=... ，seq=... 。

(当然，在fin包之前发送出去的数据，如果没有收到对应的ack确认报文，主动关闭方依然会重发这些数据)

第二次挥手：服务器端收到FIN包后，发送一个确认包给对方：而后，服务器端的状态变为 "CLOSE_WAIT"

请求报文内容为：其首部中：ACK值置为1 ；ack=... 。

第三次挥手：服务器端发送一个FIN包，告诉客户端我的数据也发送完了，不会再给你发数据了：而后，服务器端的状态变为 "LAST_ACK"

请求报文内容为：其首部中：FIN 值置为1，ACK值置为1 ；ack=...

第四次挥手：客户端 接收到 服务器端发来的FIN包，发送一个ACK给服务器端，状态转换为："TIME_WAIT"

服务器端接收到 客户端发来的ACK包，断开与客户端的连接

客户端处于 “TIME_WAIT”状态 2MSL 时间后，也断开连接，进入"CLOSE"状态

至此，完成四次挥手

---

三次握手发生在 connect()函数 和  accept() 函数中：我们先了解到大致的过程，而后分析源码：

服务器端接收到 connect()函数实现的对服务器端的连接请求后，accept()函数与之交互：

connect()函数调用时：

由于服务器端的ip和port都已经作为地址参数传入给connect()，因此，第一次握手时，connect()函数去封装好一个SYN包，并且在该SYN包中也写明了 seq内容、window 大小等一系列后续数据传输的参数信息，并将自己的状态置为 SYN_SEND；第二次握手时，首先判断自己socket()此时状态是“SYN_SEND”，而后接受服务器端返回的ACK包，解析出ACK应答包中的通信socket的具体内容，

客户端通过这个函数获得对端的地址信息（ip地址和端口号），另外本地ip地址也是在这个函数中指定的。三次握手阶段起于 connect 函数

自动绑定一个端口号，客户端自动绑定端口号是在connect函数中实现的

【我的问题的回答：socket的accept函数解析以及服务器和多个客户端的端口问题_accept能连接几个客户端_L未若的博客-CSDN博客】

首先在内存中malloc出一个新的socket空间用于与此次连接请求的客户端链接通信，而这个新的

请求报文内容为：其首部中：FIN 值置为1，ACK值置为1 ；ack=...

接收数据的序列号问题：

SYN 和 FIN 都有seq序号）

NOTE：
（1）主动端出现大量的FIN_WAIT1时需要注意网络是否畅通、出现大量的FIN_WAIT2需要仔细检查程序为何迟迟收不到对端的FIN（可能是主动方或者被动方的bug）、出现大量的TIME_WAIT需要注意系统的并发量/socket句柄资源/内存使用/端口号资源等。
（2）被动端出现大量的 CLOSE_WAIT 需要仔细检查为何自己迟迟不愿调用close关闭连接（可能是bug，socket打开用完没有关闭）
————————————————
版权声明：本文为CSDN博主「hkhl_235」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/hkhl_235/article/details/79721645

TCP协议三次握手_三次握手协议_小何在线的博客-CSDN博客

被鹅厂面怕了：TCP 连接异常的问题 - 知乎 

序列号 seq应答没有处理