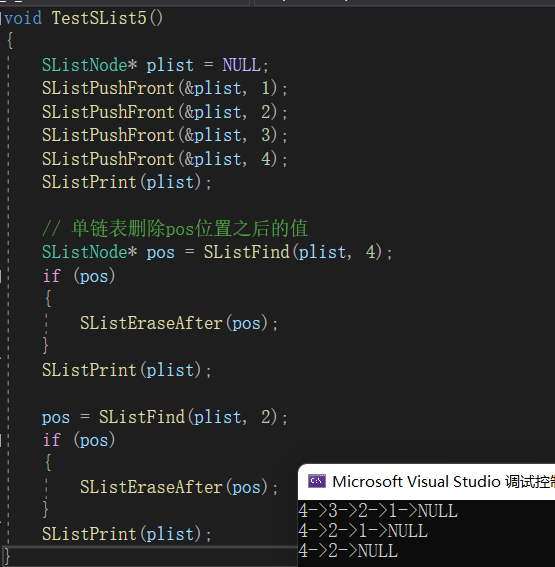
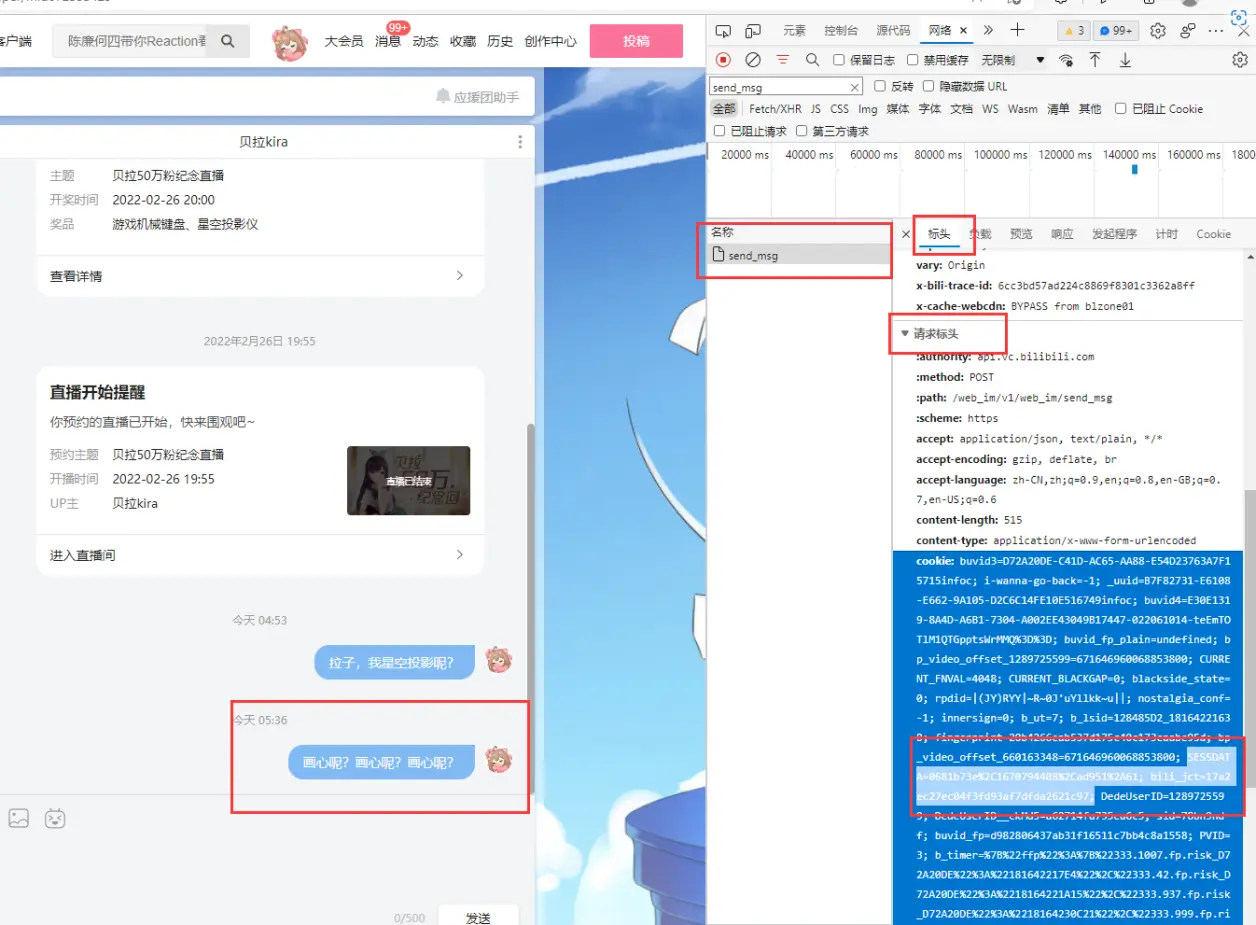
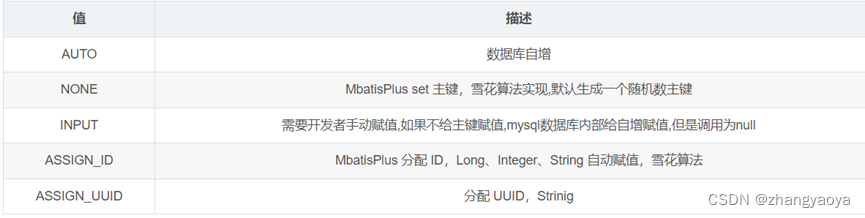
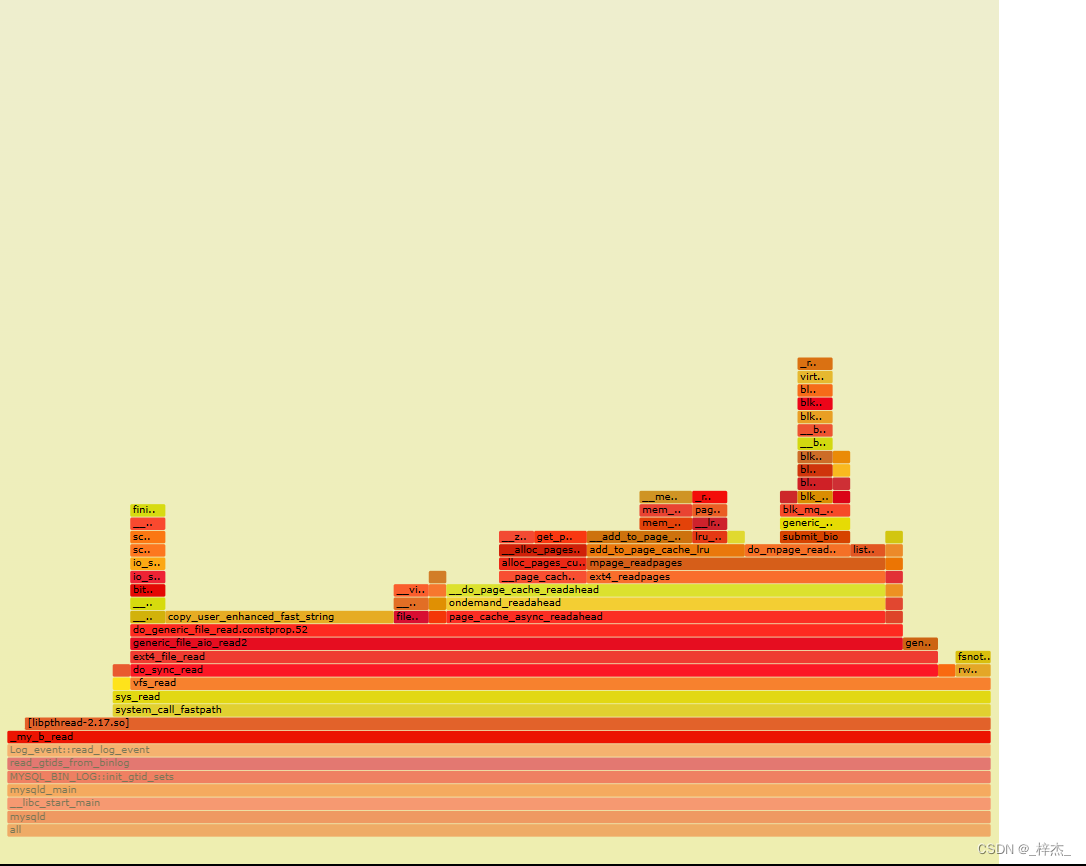
光滑道路是一个映射，但我们通过光滑道路的这个名词，可以想象成一个曲线。然后这个曲线上就会有一个速度的概念，这个速度在不同道路上（但都经过同一个点x_0）会有不同的方向，他们组成的空间就是切空间。速度就是切向量。 

如果不考虑刚才的形式，那么切空间就是有点x0和线性空间Rn组成的有序对。有序对给我的感觉就是一个映射了。确实切空间本质上也是一个映射。后面我们会看到这个映射具体对应的输入和输出。包括它的基。M是流形，图册就是覆盖这个流形的Rn空间组成的图的集合。现在我们要定义流形上的切向量和切空间，我们就需要利用图册来建立关联。

是流形上的一个小邻域，包含点的每一张图，它的参数域（R^n空间中的t）中的道路和流形上的道路是一一对应的。就是说流形上的道路和参数域上的道路的映射关系：一般代表R^n空间到流形上的映射。那么我们的p(t)在它的逆映射下可以映射到我们的R^n空间，这样就和普通的R^n空间的道路对应起来了，那么响应的切空间和切向量也就对应起来了。

 

 所以，我们在图()中，找到对应的切向量,x_i表示t0时刻经过的每一条不同的道路，它的导数就是对应的切向量，由这些切向量组合起来的就叫切空间。所以流形M的切向量在不同图中的坐标形式，就是对应R^n空间中的上述表示形式。如果两个图册还存在一个光滑互逆的映射，那么我们就可以推导得出(2),(3)

 

所以，流形M的切向量表示我们通过图册，找对一堆图，他们之间课通过前面的公式（3）建立关系。所以，对于任意一个流形上的切向量，它的不同的坐标表示形式可以用雅克比矩阵进行转换。 

这个意思是说，我们找到了流形上的切空间，它和图上的（R^n）切空间相对应，而且线性结构和坐标形式是对应的。选择不同的图，这个线性结构并不会发生变化。

 

这一段非常重要，首先我们找到一个道路，然后道路上的一个点x0的邻域上，我们定一个一个函数f(x0),然后f的在x0的方向导数（选取了一个切向量）。这就是f的微分。这里其实让我有了新的认识，之前一致觉得切向量是建立在f上的，现在看来，切向量是建立在道路上的。即便没有f，那么我们也可以有道路以及道路上的切向量和切空间，在道路上的邻域选取一个f后，在进行方向导数的偏导的计算，就是f的微分。现在还没有引入基和余切空间，我们后面看是怎么对应上的。

 

所以，首先我们要确定一个道路，然后找到切向量，这样就可以定义一个泛函，它是映射f到R的映射，输入是一个映射f，它定义在道路上的一个函数，它本身也是一个泛函。同时，他们的线性关系是由切向量决定的。所以切空间和微分的线性空间存在同构关系。

 

切空间是函数f(x)上满足（8）（9）关系的函数（微分）的线性空间。

 

前面我们说了，切空间和微分空间是同构的，那么必然存在一个两者之间的一一映射关系。我们的方向导数，如果只是求偏导，不考虑切向量，其实就是f只对x求导，忽略x对t求导，那么就相当于后面那个方向导数是1，也可以这么理解，我们找到切空间的标准向量基，e1,e2....en,那么取这些基作为方向导数，那么最终的微分就单纯变成了求偏导。有点绕，举个例子：

然后如果你取切向量为e1,那么相当于就是0了，那么上面就是

因为e1的坐标就是1，所以你就看到了e1和f'(x1）的对应关系，所以我们终于找到了切空间的一组基。从向量角度，他是e1,e2,...en，从泛函角度，它就是求偏导，因为我们改变切向量，对应的泛函改变的是求偏导操作，和f无关。

这里也要好好理解，流形上的F，是一个定义在流形道路上的函数f，它的微分运算具有(8)(9)的形式，那么他们肯定包含切向量，这个切向量是微分中需要用到的。而把（9）里面的x换成p，其实我们就定义了流形本身上面的微分，它是和坐标无关的，也不需要引入局部坐标形式。

 

 算子l（其实就是微分）在局部坐标(x1,x2...xn)下，也就是说选取了一个道路，具有偏导向量导数的形式。这个时候还没选具体的道路上的函数f。而具体的切向量下是有一个坐标的，是切向量的坐标。后面是坐标转换公式，它和前面的公式形式是一样的。

 现在要考虑余切空间了，为什么要引出这个呢，是因为我们前面已经对切向量和切空间有一个很好的认识，也从线性泛函上好好的理解了切空间的基。包括切向量形式下的坐标基，和泛函空间中的坐标基。

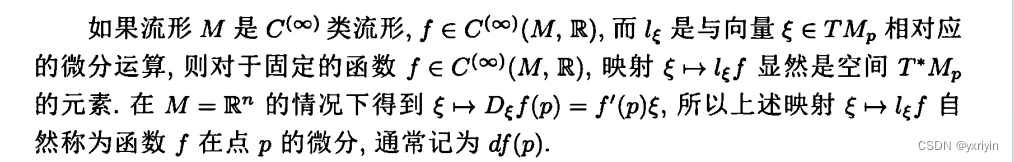
f是定义在道路x上的函数，在流形的概念里，应该是流形M上的道路上的函数。l_xi是微分运算，它需要一个对应的切向量。这里要注意，我们需要固定一个函数f，然后才能建立切向量到lf的映射。它是切空间的对偶空间。这里要注意，我们的这个对偶空间，需要提供一个固定的f，然后加上微分运算，就得到了函数f在p的微分。

 

 这里引出了切空间的对偶基。看上去符号虽然是我们熟悉的dx(偏导x)=(0或者1）,但暂时还没看出它和微分的直接关系。后面的坐标转换公式就是雅克比矩阵。

所以我们再看下，对于切空间中的向量，我们的余切空间提供了一个固定函数，或者说对于一个固定的函数f，余切空间是把切向量的每个分量分别作用在f上，然后再相加，有点类似于内积的操作。所以这组基dx我们可以这么看，对于固定的f，这组基中的一个分量，会吧其中切向量的一个分量给取出来，也就是f对某一个x的偏导。所以，虽然切向量的每个分量看上去也是个偏导，但他因为没有固定的函数，而且是一个“向量”，所以还需要余切空间的帮忙，对应一个固定的f，同时也引入内积的部分，得到一个R。

 这里的m次微分形式，感觉应该是微分的微分的微分。。。。持续下去。但具体我还得看看。不过这个微分形式是作用在切空间上的。

 phy是R^n到流形的映射。这里的坐标变换是道路上的坐标的变换，而切空间的坐标变换需要求导。求导其实就是微分，也就是对切空间中的切向量进行内积操作（对于固定的f）。所以这是在对偶空间下进行的。

 

这里意思是，流形上的微分形式w，在具体的图中的表现形式的转移，它是通过一个phy的对偶空间来实现的。 这么说吧，w是微分形式，微分形式的转移是发生在微分上的，也就是切向量的对偶空间上，就是求导后的对空间。

前面解释了，微分形式的转移是发生到微分上，也就是切向量的对偶空间上，所以它是一个函数，也就是系数都是函数。