题目

给定一个正整数数组 nums和整数 k ，请找出该数组内乘积小于 k 的连续的子数组的个数。

示例 1:

输入: nums = [10,5,2,6], k = 100
输出: 8
解释: 8 个乘积小于 100 的子数组分别为: [10], [5], [2], [6], [10,5], [5,2], [2,6], [5,2,6]。
需要注意的是 [10,5,2] 并不是乘积小于100的子数组。

示例 2:

输入: nums = [1,2,3], k = 0
输出: 0

提示:

1 <= nums.length <= 3 * 104
1 <= nums[i] <= 1000
0 <= k <= 106

解题思路

前置知识

滑动窗口

（1）滑动窗口可以用以解决数组/字符串的子元素相关问题，并且可以将嵌套的循环问题，转换为单循环问题，从而降低时间复杂度。故滑动窗口算法的复杂度一般为 O(n)。

（2）滑动窗口的基本思想如下：

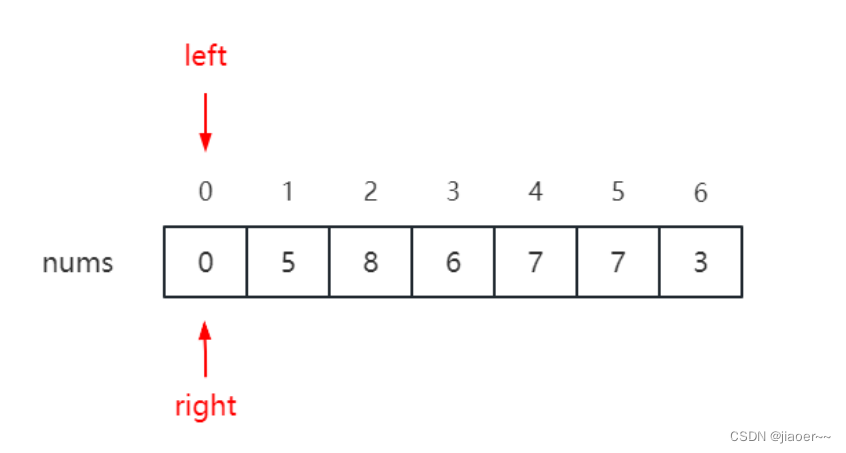
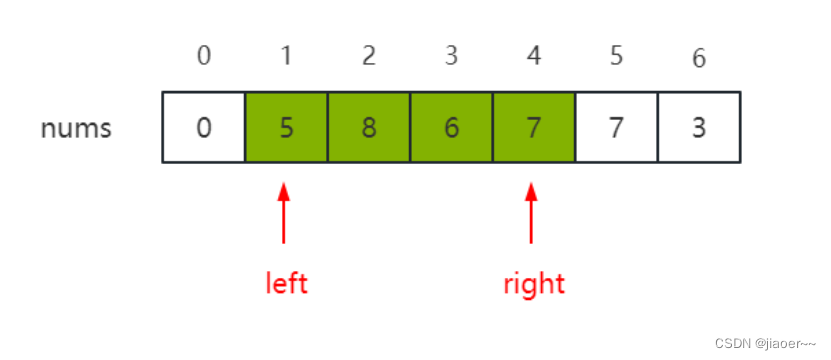
首先使用双指针维护一个子数组，别称为 left 和 right。left 指向窗口的左端点，right 指向窗口的右端点。如下图所示：

窗口随着 right 指针向右滑动开始遍历整个数组区间（即增大窗口）；

而在每次迭代内部（即针对每一次 right）要对子数组区间是否满足要求进行判断。如果子数组区间不能够满足条件则将 left 指针向右移动（即缩小窗口），这样窗口就实现了向右滑动。

知道了滑动窗口后，我们来看一下这道题

1.题目要求我们求出数组内乘积小于 k 的连续的子数组的个数，一般求解子数组这类题我们都会用到滑动数组，这道题也不例外

2.首先我们设置好要用到的变量，curr 用来存放子数组的乘积，sum 用来统计符合条件的子数组的个数，i 作为滑动窗口中窗口的左边界。

3.我们for循环对数组进行遍历，每当 j 遍历一个元素后就把它乘进 curr 中，然后用while循环去判断这个滑动窗口内的乘积是否大于k，若大于k 我们就将滑动窗口最左边的一个元素从curr中除去，并将滑动窗口的左边界向右移动一个，直到滑动窗口内的乘积小于k，我们就把结果加到sum中，注意这里的 right - left + 1 就是以当前窗口右界为最后一个元素的连续子序列的个数。这么做的道理是这样的。如果一个长度为 n 的序列中的任意长度连续子序列都满足要求，那么这些子序列可以无重复无遗漏地划分为 n 组，组内子序列尾元素相同，组间尾元素互异。

举个例子：
思路: 设存在数组nums=[A, B, C, D], k为乘积, count为符合条件的数组个数, i,j为窗口左右边界;
     *(假设) A: A<k    i=j=0  --> count = A (0-0+1)
     *      B: AB<k   j=1    --> count = AB, B(1-0+1)
     *      C: ABC>=k j=2    --> BC<k i=1 --> count = BC, C (2-1+1)
     *      D: BCD>k  j=3    --> CD>K i=2 --> D < k i=3 --> count = D (3-3+1)
     *      当计算的数组乘积大于k时，将窗口左边界右移, 直到小于k, 计算count，窗口右边界右移；
     *      当计算的数组乘积小于k时，计算count，窗口右边界右移
     *      得出规律：每一次遍历count增加了j-i+1
4.最后返回sum即可。

代码实现

class Solution {
    public int numSubarrayProductLessThanK(int[] nums, int k) {
        int n = nums.length;
        int curr = 1, sum = 0, i = 0; 
        for(int j = 0; j < n; j++){
            curr *= nums[j];
            while(i <= j && curr >= k ){
                curr /= nums[i];
                i++;
            }
            sum += j - i + 1;
        }
        return sum;
    }
}