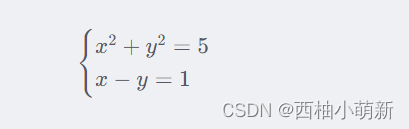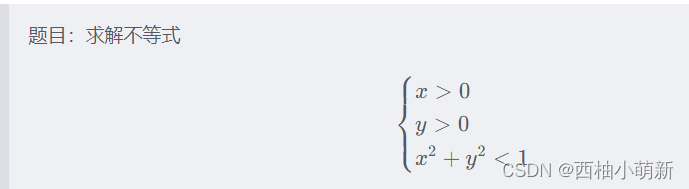目录
1.用法结构
2.解单变量方程
3.解多变量方程
4.解带参方程
5.解不等式
6.总结
1.用法结构
solve函数是MATLAB中的一个符号计算函数,用于求解方程组或方程的符号解。
它的用法如下:
定义符号变量:使用syms函数定义符号变量,例如:syms x y z;
定义方程或方程组:将方程或方程组表示为符号表达式,例如:eq1 = x^2 + y^2 == 1;
调用solve函数:使用solve函数求解方程或方程组的符号解,例如:sol =solve(eq1, [x, y]);
其中,第一个参数是方程或方程组,第二个参数是未知数的符号变量。
solve函数返回的是一个结构体数组,每个元素对应一个符号解。
使用solve函数时,需要先定义变量为符号变量,可以使用syms函数来定义符号变量。
2.解单变量方程
题目:求解方程
2 x + 1 = 0
syms x eqn = 2*x + 1 == 0; x = solve(eqn, x)
3.解多变量方程
题目:求解方程
syms x y eqns = [x^2 + y^2 == 5, x - y == 1]; vars = [x y]; [x, y] = solve(eqns, vars)
4.解带参方程
syms a b c x eqn = a*x^2 + b*x + c == 0; x = solve(eqn, x)
5.解不等式
syms x y cond1 = x > 0; cond2 = y > 0; cond3 = x^2 + y^2 < 1; conds = [cond1 cond2 cond3]; sol = solve(conds, [x y], 'ReturnConditions', true); sol.x sol.y sol.conditions
其中,sol.x & sol.y 会输出新的变量,sol.conditions新变量之间满足的关系 。
6.总结
常规语法:sol = solve(eqn,var)
当公式中的解无法有限列举出来时,需要用参数化表示,就要用下列语法:
[y1,…,yN,parameters,conditions] = solve(eqns,vars,‘ReturnConditions’,true)
(通过将 "ReturnConditions选项指定为true, 可以找到同一公式的完整解。)