🍉 吃瓜系列 教材:《机器学习》 周志华著
🕒时间:2023/7/26
目录
一、对数几率回归
1.1 定义和基本思想
1.2 对数记录回归建模
1.3 广义线性模型
1.3.1 指数族分布
1.3.2 广义线性模型的三条假设
1.4 对数几率回归的广义线性模型推导
1.5 最大似然估计
1.6 对数几率回归的参数估计(公式推导)
一、对数几率回归
1.1 定义和基本思想
定义:
对数几率回归(Logistic Regression)是一种常用的分类算法,主要用于将样本根据特征分成不同的类别。
线性回归模型返回的是一个实值
但是分类问题返回的是一个概率
基本思想是:
通过对数据进行建模,得到一个函数,将输入特征映射到一个概率值,该概率表示样本属于某一类别的概率。
具体来说,对数几率回归首先使用线性函数拟合输入特征,然后对线性函数的输出结果应用一个逻辑函数(sigmoid函数),将输出结果映射到0到1之间的概率值,进而进行分类。
优缺点:
对数几率回归有以下优点:
1. 运算速度快,适用于大规模数据集;
2. 不需要对输入数据做太多假设,表现较为稳定;
3. 输出结果为概率值,能够给出明确的分类结果。
但是,对数几率回归也存在以下缺点:
1. 对于非线性可分的数据,分类效果不佳;
2. 对于特征空间的高维度数据,容易出现“过拟合”情况,需要进行正则化处理;
3. 对噪声比较敏感。
1.2 对数几率回归建模
因为单位跃迁函数是不连续的函数,在数据处理的时候比较困难
所以在此使用了一个替代函数
在机器学习中,我们通常使用对数几率函数去做一个替代函数

这种方法有很多优点,例如它是直接对分类可能性进行建模无需事先假设数据分布,这样就避免了假设分布不准确所带来的问题
它不是仅预测出“类别”,而是可得到近似概率预测,这对许多需利用概率辅助决策的任务很有用:
此外对率函数是任意阶可导的凸函数,有很好的数学性质,现有的许多数值优化算法都可直接用于求取最优解


对数几率的由来


得到 3.23 3.24 两个式子之后,对数几率回归的建模就算完成了!
1.3 广义线性模型
1.3.1 指数族分布

证明伯努利分布属于指数族分布


这里变形的依据是:

再次拆分成加法
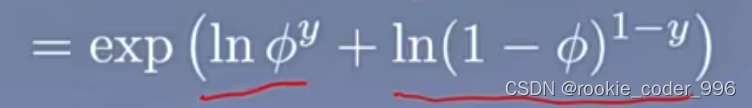
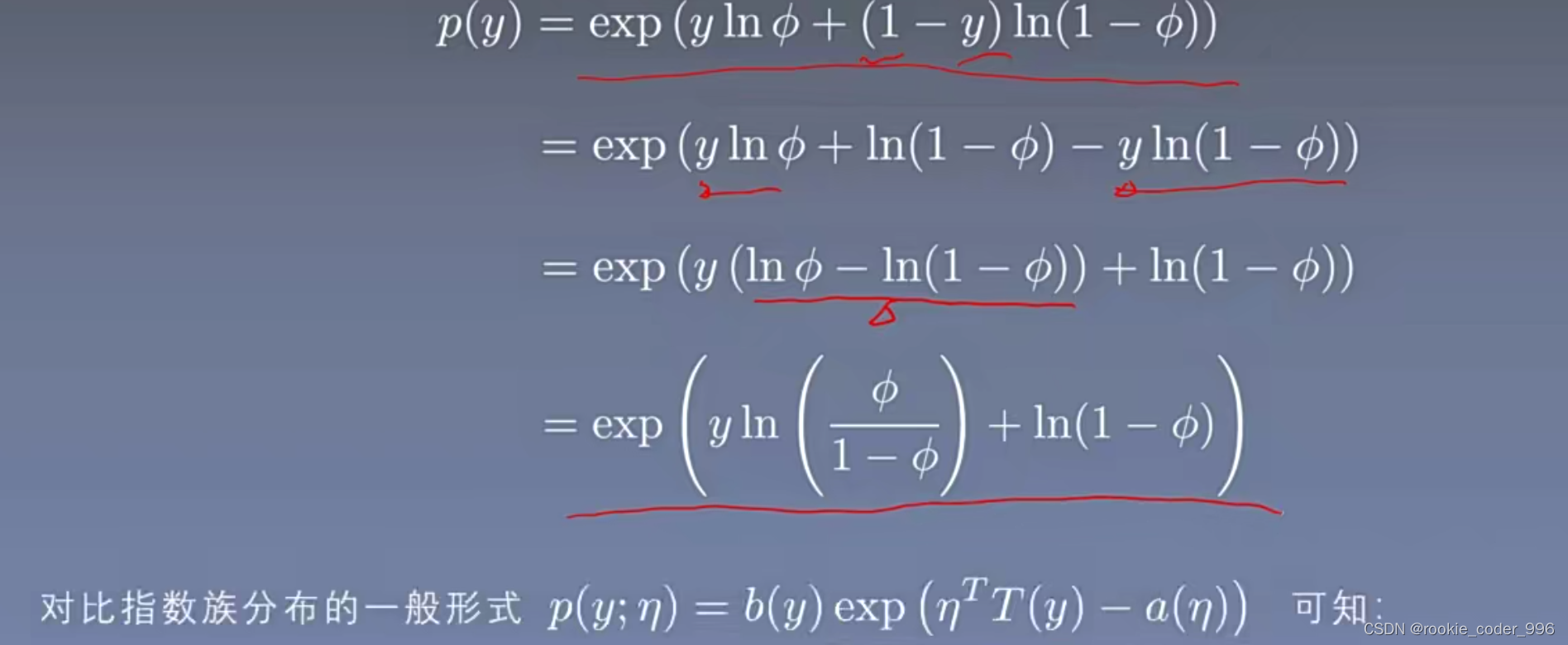
对比指数分布的一般形式得出对应的参数

1.3.2 广义线性模型的三条假设
广义线性模型的三条假设:
1. 在给定 x 的条件下,假设随机变量 y 服从某个指数族分布
2.在给定 x 的条件下,我们的目标是得到一个模型 h(x)能预测出T(y)的期望值
3.假设该指数族分布中的自然参数 n 和 x 呈线性关系
即
1.4 对数几率回归的广义线性模型推导

使用上面的三个假设


而 E[ y|x ] = E[ y ]
y 是服从伯努利分布的 所以期望是很好求出来的
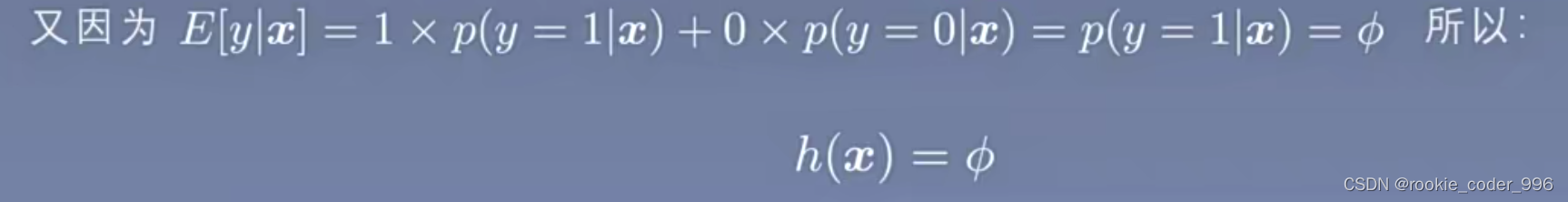
到此处,假设3 还没有用上


1.5 最大似然估计
最大似然估计


上面的转化,把累乘转换换成了累加
似然函数就转换成了对数似然函数
这样的话后续的求导会很方便

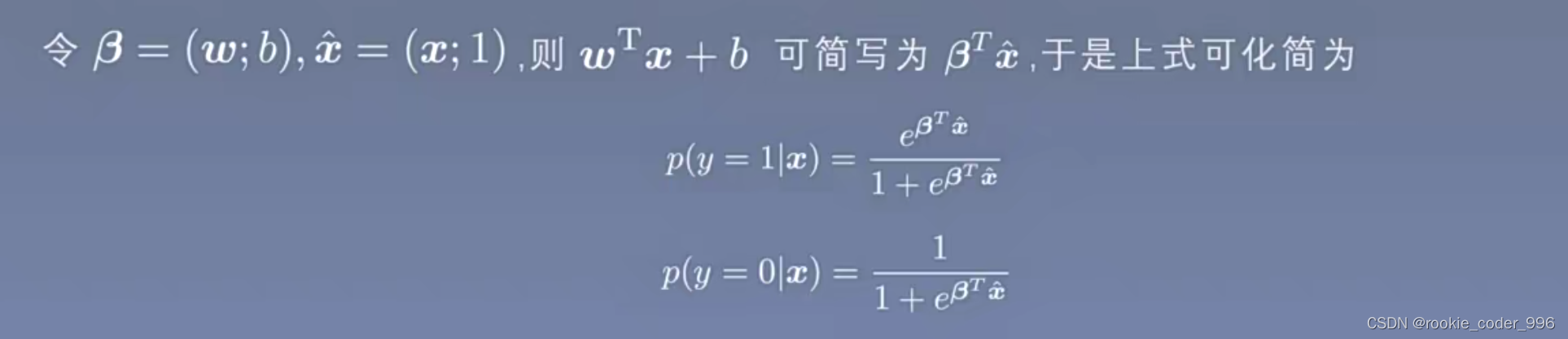

或者

这个式子相比于 3.26式子更容易进行公式的推导
1.6 对数几率回归的参数估计(公式推导)
- 先使用 3.26 进行公式推导
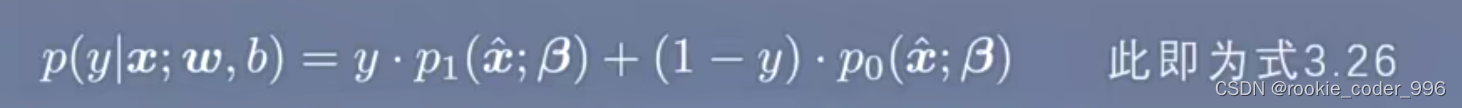



综合整理一下
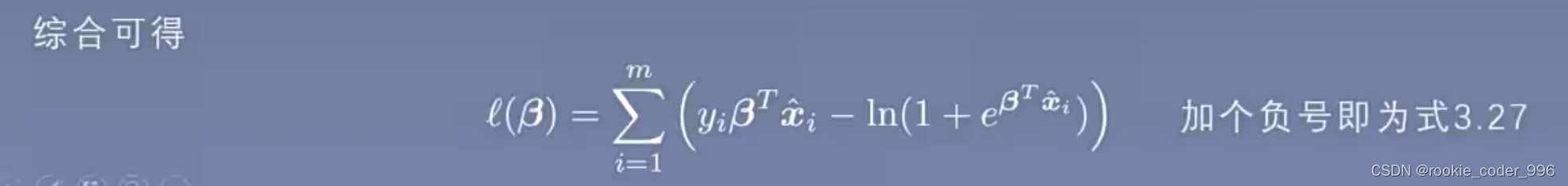
似然函数是求最大值的
损失函数求最小值,所以加一个负号 得到式子 3.27
- 另一种公式推导(更容易推导一点)


似然函数是求最大值的
损失函数求最小值,所以加一个负号 得到式子 3.27